Verwenden Sie Addition oder Subtraktion, um die minimale Anzahl von Schritten für N bei jedem Schritt zu erhalten

Aus der obigen Problemstellung besteht unsere Aufgabe darin, die Mindestanzahl von Schritten zu ermitteln, in denen wir durch Addition oder Subtraktion jeweils die gegebene Zahl N erhalten können. Wir können verstehen, dass wir die Mindestanzahl der Schritte, die ausgeführt werden können, und die Reihenfolge der Schritte für jede gegebene ganze Zahl N ausdrucken müssen, indem wir die Schrittnummern addieren und subtrahieren, um eine Zahl beginnend bei 0 zu erhalten.

In diesem Aufgabensatz können wir bei jedem Schritt eine Zahl addieren oder subtrahieren, die der Anzahl der Schritte zur aktuellen Position entspricht. Beispielsweise können wir in Schritt 1 1 oder -1 hinzufügen. Außerdem können wir in Schritt 2 2 oder -2 hinzufügen und so weiter. Je nach Situation können wir bei jedem Schritt Zahlen addieren oder subtrahieren.

Die größte Herausforderung dieses Problems besteht darin, dass wir die Mindestanzahl an Schritten beginnend bei 0 ausführen müssen, um N zu erreichen. Lassen Sie uns dieses Problem anhand eines Beispiels besser verstehen.

Das unten angegebene Beispiel zeigt Ihnen jede Zahl, die wir in zwei Schritten beginnend bei 0 erhalten können, indem wir die oben genannten Operationen ausführen.

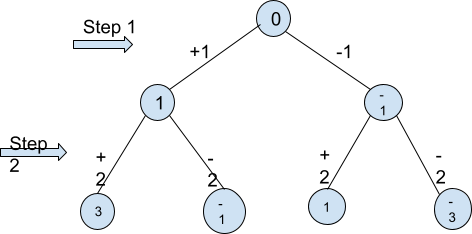
Angenommen, wir haben N=1.

Ausgabe

Minimum no of steps: 1
Sequence of steps: 1

Anleitung

Wir können 1 auf zwei Arten erreichen –

• Fügen Sie einfach 1 zu Schritt 1 hinzu, um von 0 auf 1 zu gelangen, was 1 Schritt dauert.

• Subtrahieren Sie 1 in Schritt 1, um von 0 auf -1 zu gelangen, und addieren Sie dann 2 in Schritt 2, um von -1 auf 1 zu gelangen, was 2 Schritte dauert.

Da die Frage besagt, dass wir die Mindestanzahl an Schritten benötigen, um eine beliebige Zahl N zu erreichen, ist die gewünschte Ausgabe für diese Eingabe 1.

Für N=3

Ausgabe

Minimum no of steps: 2
Sequence of steps: 1 2

Anleitung

Wir addieren 1 in Schritt 1, um von 0 auf 1 zu gelangen, und fügen dann 2 in Schritt 2 hinzu, um von 1 auf 3 zu gelangen.

Methode

Der beste Weg, das Problem zu lösen, besteht darin, zunächst herauszufinden, ob N positiv oder negativ ist. Wir müssen die entsprechende Anzahl an Schritten addieren bzw. subtrahieren, um das Problem zu lösen.

• Wenn N eine positive Zahl ist, füge weitere Schritte hinzu, bis die Summe größer oder gleich N ist.

• Wenn N negativ ist, subtrahieren Sie die Anzahl der Schritte entsprechend weiter, bis die Summe größer oder gleich N ist.

• Wenn die Summe im obigen Fall gleich N ist, geben Sie die Anzahl der Schritte und die Reihenfolge der Schritte zurück. Das Hauptproblem besteht darin, mit der Situation umzugehen, wenn N überschritten wird.

Sobald die Summe N überschreitet, prüfen Sie, ob (Summe-N) gerade oder ungerade ist.

• Wenn (Summe-N) gerade ist, müssen wir die Subtraktion in Schritten von (Summe-N)/2 durchführen, um N zu erhalten.

  Lassen Sie uns diesen Fall anhand eines geeigneten Beispiels besser verstehen.

  Für N=8

  1+2+3+4=10, also mehr als 8.

  Weil 10-8=2 eine gerade Zahl ist. Wir subtrahieren also in Schritten von 2/2, also

  Schritt 1. Die Reihenfolge der Schritte ist also -1 2 3 4 und das Minimum

  Die Anzahl der Schritte, um N zu erreichen, beträgt 4.

• Wenn (Summe-N) eine ungerade Zahl ist, bestimmen Sie zunächst, ob die Zahl, deren Summe im vorherigen Schritt N überschreitet, gerade oder ungerade ist.

  Wenn der vorherige Schritt ungerade war, führen Sie einen Schritt aus, indem Sie die nächste Schrittnummer hinzufügen, wodurch unsere (Summe-N) gerade wird, und führen Sie dann die oben genannten Schritte aus, um das gewünschte Ergebnis zu erhalten.

  Zum Beispiel N=9

  1+2+3+4=10, was mehr als 9 ist.

  Weil 10-9=1 ist, ist dies eine ungerade Zahl. Der nächste Schritt ist 5, was eine ungerade Zahl ist, also machen wir einfach einen Schritt und addieren 5 zur Summe, um 15 zu erhalten, was (Summe-N)=6 ergibt. Wenn Sie die Subtraktion in Schritt 3 durchführen, erhalten Sie die Sequenz 1 2 -3 4 5, die die gewünschte Ausgabe darstellt.

  Angenommen, der vorherige Schritt ist eine gerade Zahl. In diesem Fall müssen wir zwei Schritte ausführen, den i-ten Schritt addieren und den (i+1) Schritt subtrahieren, um (Summe-N) als gerade Zahl zu erhalten die gewünschte Schrittfolge.

  Für N=5

  1+2+3=6, mehr als 5.

  Da (sum-N) =1, betrachten wir den letzten Schritt, wenn su die Zahl N überschreitet. Da es sich um eine gerade Zahl handelt, führen wir zwei Schritte aus, Schritt 4 und Schritt 5. Unsere Aufgabe besteht darin, (Summe-N) gleichmäßig zu machen. Indem wir in Schritt 4 addieren und in Schritt 5 subtrahieren, können wir (Summe-N) erhalten, selbst wenn 1 von der Summe subtrahiert wird. Da (Summe-N) gleich 0 ist, erhalten wir N. Daher ist die Reihenfolge 1 2 3 4 -5.

Beispiel

Hier ist der C++-Code für die Methode -

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
void minimumStep(int n){
   vector <int> steps; // for storing the sequence
   int totalSum=0; 
   int temp=0;
   if(n>=0){   // if n is positive then temp will store positive
      temp=1;
   } else {
      temp=-1;  // n is negative then temp will store negative
   }
   n=abs(n);
   int step=0;
   for(step=1;totalSum<n;step++){  // for storing the steps till sum is not greater than n
      steps.push_back(temp*step);
   
      totalSum=totalSum+step;
   }
   if(totalSum>temp*n) {  //when sum greater than n 
      if(step%2==0) {   //when step is even 
         totalSum=totalSum-n; 
         if((totalSum)%2!=0) { // when totalSum-n is odd
            steps.push_back(temp*step);  //store the addition of next step 
            steps.push_back((temp*-1)*(step+1));  // store the subtraction of next step 
            totalSum--;  //make totalSum even
         }
         int check=(totalSum)/2;
         check--;
         steps[check]=steps[check]*-1; 
		} else {        //when step is odd
         totalSum=totalSum-n;
         if((totalSum)%2!=0)  {  // when totalSum-n is odd 
            steps.push_back(temp*step);   //store the next addition value 
            totalSum+=step; 
            step++;
         }
         int check=(totalSum)/2;
         check--;
         steps[check]=steps[check]*-1;
   
      }
   }
   //print the minimum number of steps taken 
   cout<<"The minimum number of steps : "<<steps.size()<<endl;
   //print the steps is stored in vector
      cout<<"Sequence of steps : ";
   for(int i=0;i<steps.size();i++){
      cout<<steps[i]<<" ";
   }
   
}
int main(){
   int m=17;
   minimumStep(m);
   
   return 0;
}

Ausgabe

The minimum number of steps : 6
Sequence of steps : 1 -2 3 4 5 6

Zeitliche Komplexität: O(sqrt(N))

Raumkomplexität: O(sqrt(N))

Fazit

In diesem Artikel versuchen wir, die Methode zu erklären, mit der man die Mindestanzahl an Schritten ermittelt, um N zu erreichen, indem man bei jedem Schritt addiert oder subtrahiert und die Sequenz ausgibt. Ich hoffe, dass dieser Artikel Ihnen hilft, dieses Konzept besser kennenzulernen.

Das obige ist der detaillierte Inhalt vonVerwenden Sie Addition oder Subtraktion, um die minimale Anzahl von Schritten für N bei jedem Schritt zu erhalten. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!