Was ist das C/C++-Programm für die n-te katalanische Zahl?

Katalanische Zahlen sind eine Reihe von Zahlen. Katalanische Zahlen sind eine Folge natürlicher Zahlen, die in einer Vielzahl von Zählproblemen vorkommen und häufig rekursiv definierte Objekte beinhalten.

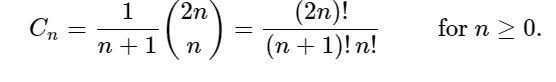
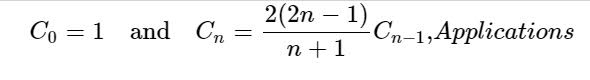
• C_n ist die Anzahl der Dyck-Wörter mit der Länge 2n. Ein Dyck-Wort ist eine Zeichenfolge, die aus n Xs und n Ys besteht, sodass die Anzahl der Ys die Anzahl der Xs in keinem Anfangsfragment der Zeichenfolge übersteigt. Das Folgende ist beispielsweise ein Dyck-Wort der Länge 6:

XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY.

• interpretiert das Symbol neu. Die Menge

  ((())) ()(()) ()()() (())() (()())

  Nach dem Login kopieren

C
• n

  ist die Anzahl der verschiedenen Arten, auf die n + 1 Faktoren sein können vollständig umschlossen (oder die Anzahl der Möglichkeiten, auf denen n Anwendungen zugehöriger binärer Operatoren möglich sind). Beispielsweise haben wir für n = 3 fünf verschiedene Klammern für die folgenden vier Faktoren:

  ((ab)c)d (a(bc))d (ab)(cd) a((bc)d) a(b(cd))

  Nach dem Login kopieren

Aufeinanderfolgende Anwendungen binärer Operatoren können durch einen vollständigen Binärbaum dargestellt werden. (Ein verwurzelter Binärbaum gilt als vollständig, wenn jeder Scheitelpunkt entweder zwei untergeordnete Knoten oder keine untergeordneten Knoten hat.) Daraus ergibt sich, dass C
• n

  die Anzahl der vollständigen Binärbäume mit n + 1 Blättern ist:

Beispiel

- 6

- 1 1 2 5 14 42Erklärung

Wenn n = 0, 1, 2, 3,4,5,6,7,8,9,10 , .. ., die ersten n katalanischen Zahlen sind

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862,

Beispiel

#include<iostream>
using namespace std;
long int catalan( int n) {
   if (n <= 1){
      return 1;
   }
   long int result = 0;
   for (int i=0; i<n; i++){
      result += catalan(i)*catalan(n-i-1);
   }
   return result;
}
int main(){
   for (int i=0; i<6; i++)
   cout << catalan(i) << " ";
   return 0;
}

Ausgabe

1 1 2 5 14 42

Das obige ist der detaillierte Inhalt vonWas ist das C/C++-Programm für die n-te katalanische Zahl?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!