Hier erfahren Sie, wie Sie die Fläche eines n-seitigen regelmäßigen Polygons mit gegebenem Radius berechnen. Der Radius ist hier der Abstand von einem beliebigen Scheitelpunkt zum Mittelpunkt. Um dieses Problem zu lösen, zeichnen wir eine vertikale Linie von der Mitte zu einer der Seiten. Nehmen Sie an, dass die Länge jeder Seite „a“ ist. Die Senkrechte teilt die Seite in zwei Teile, wobei jeder Teil die Länge a/2 hat. Eine vertikale Linie und ein Radius bilden einen Winkel x. Angenommen, die Länge des Radius beträgt h.
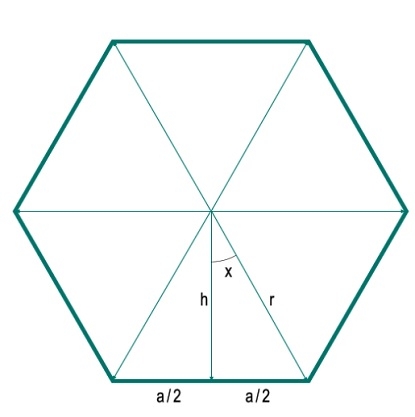
Hier können wir sehen, dass das Polygon in N gleiche Dreiecke unterteilt ist. Daher wird jedes Polygon mit N Seiten in N Dreiecke unterteilt. Daher beträgt der Winkel in der Mitte 360 Grad. Dieser wird in 360°/N verschiedene Winkel aufgeteilt (hier 360°/6 = 60°). Daher beträgt der Winkel x 180°/N. Jetzt können wir h und a mithilfe trigonometrischer Gleichungen leicht ermitteln.
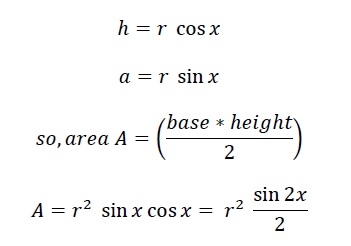
Jetzt beträgt die Fläche des gesamten Polygons N*A.
#include <iostream>
#include <cmath>
using namespace std;
float polygonArea(float r, int n){
return ((r * r * n) * sin((360 / n) * 3.1415 / 180)) / 2; //convert
angle to rad then calculate
}
int main() {
float rad = 9.0f;
int sides = 6;
cout << "Polygon Area: " << polygonArea(rad, sides);
}Polygon Area: 210.44
Das obige ist der detaillierte Inhalt vonWie groß ist die Fläche eines n-seitigen regelmäßigen Polygons mit einem gegebenen Radius?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
