
Obwohl DNNs in verschiedenen praktischen Anwendungen große Erfolge erzielt haben, werden ihre Prozesse oft als Black Boxes betrachtet, da es schwierig ist zu erklären, wie DNNs Entscheidungen treffen. Die mangelnde Interpretierbarkeit beeinträchtigt die Zuverlässigkeit von DNNs und behindert so ihre breite Anwendung bei anspruchsvollen Aufgaben wie autonomem Fahren und KI-Medizin. Daher haben erklärbare DNNs zunehmend Aufmerksamkeit erregt.
Als typische Perspektive zur Erklärung von DNN zielt die Attributionsmethode darauf ab, die Attributions-/Wichtigkeits-/Beitragsbewertung jeder Eingabevariablen zur Netzwerkausgabe zu berechnen. Bei einem vorab trainierten DNN für die Bildklassifizierung und einem Eingabebild bezieht sich der Attributwert für jede Eingabevariable beispielsweise auf den numerischen Einfluss jedes Pixels auf den Klassifizierungskonfidenzwert.
Obwohl Forscher in den letzten Jahren viele Attributionsmethoden vorgeschlagen haben, basieren die meisten davon auf unterschiedlichen Heuristiken. Derzeit fehlt eine einheitliche theoretische Perspektive, um die Korrektheit dieser Attributionsmethoden zu überprüfen oder zumindest ihre Kernmechanismen mathematisch aufzuklären.
Forscher haben versucht, verschiedene Attributionsmethoden zu vereinheitlichen, aber diese Studien haben nur wenige Methoden abgedeckt.
In diesem Artikel schlagen wir eine „einheitliche Erklärung der intrinsischen Mechanismen von 14 Algorithmen zur Wichtigkeitszuordnung von Eingabeeinheiten“ vor.

Papieradresse: https://arxiv.org/pdf/2303.01506.pdf
In der Tat, ob es sich um „12 Algorithmen zur Verbesserung der Migrationsresistenz“ oder „14 Eingaben“ handelt „Unit Importance Attribution Algorithm“ sind die am stärksten betroffenen Bereiche der technischen Algorithmen. In diesen beiden Bereichen sind die meisten Algorithmen empirisch. Menschen entwerfen einige plausible technische Algorithmen basierend auf experimenteller Erfahrung oder intuitivem Verständnis. Die meisten Studien haben keine strengen Definitionen und theoretischen Beweise dafür geliefert, „was genau die Bedeutung von Eingabeeinheiten ist“. Einige Studien haben bestimmte Beweise, aber diese sind oft sehr unvollständig. Natürlich durchzieht das Problem des „Mangels an strengen Definitionen und Demonstrationen“ das gesamte Gebiet der künstlichen Intelligenz, ist aber in diesen beiden Richtungen besonders ausgeprägt.
Natürlich ist unsere theoretische Analyse nicht nur auf die 14 Attributionsalgorithmen anwendbar und kann theoretisch weitere ähnliche Forschungen vereinheitlichen. Aufgrund der begrenzten Arbeitskapazität diskutieren wir in diesem Artikel nur 14 Algorithmen.
Die eigentliche Schwierigkeit der Forschung besteht darin, dass unterschiedliche empirische Attributionsalgorithmen oft auf unterschiedlichen Intuitionen basieren. Jede Arbeit strebt nur danach, sich aus ihrer eigenen Perspektive zu „rechtfertigen“, und zwar auf der Grundlage unterschiedlicher Intuitionen oder Perspektiven ein Mangel an einer standardisierten mathematischen Sprache, um das Wesen verschiedener Algorithmen einheitlich zu beschreiben.
Bevor wir über Mathematik sprechen, werden in diesem Artikel die vorherigen Algorithmen kurz von einer intuitiven Ebene aus betrachtet.
1. Gradientenbasierter Attributionsalgorithmus. Diese Art von Algorithmus geht im Allgemeinen davon aus, dass der Gradient der Ausgabe des neuronalen Netzwerks an jede Eingabeeinheit die Bedeutung der Eingabeeinheit widerspiegeln kann. Beispielsweise modelliert der Gradient*Input-Algorithmus die Wichtigkeit einer Eingabeeinheit als elementweises Produkt des Gradienten und des Eingabeeinheitswerts. Da der Gradient nur die lokale Bedeutung der Eingabeeinheit widerspiegeln kann, modellieren die Algorithmen „Smooth Gradients“ und „Integrated Gradients“ die Wichtigkeit als elementweises Produkt des durchschnittlichen Gradienten und des Werts der Eingabeeinheit, wobei sich der durchschnittliche Gradient in diesen beiden Methoden bezieht zum Nachbar der Eingabeprobe. Der Durchschnittswert des Gradienten innerhalb der Domäne bzw. der durchschnittliche Gradient des linearen Interpolationspunkts zwischen der Eingabeprobe und dem Basispunkt. In ähnlicher Weise berechnet der Grad-CAM-Algorithmus den Durchschnitt der Netzwerkausgabe über alle Merkmalsgradienten in jedem Kanal, um die Wichtigkeitsbewertung zu berechnen. Darüber hinaus geht der Algorithmus „Expected Gradients“ davon aus, dass die Auswahl eines einzelnen Benchmark-Punkts häufig zu verzerrten Attributionsergebnissen führt, und schlägt daher vor, die Wichtigkeit als Erwartung von Attributionsergebnissen „Integrated Gradients“ unter verschiedenen Benchmark-Punkten zu modellieren.
2. Attributionsalgorithmus basierend auf schichtweiser Backpropagation. Tiefe neuronale Netze sind oft äußerst komplex und die Struktur jeder Schicht neuronaler Netze ist relativ einfach (tiefe Merkmale sind beispielsweise normalerweise die lineare Summierung flacher Merkmale + nichtlineare Aktivierungsfunktionen), was die Analyse der Bedeutung erleichtert flache bis tiefe Merkmale. Daher ermittelt diese Art von Algorithmus die Wichtigkeit der Eingabeeinheit, indem sie die Wichtigkeit von Merkmalen mittlerer Ebene schätzt und diese Wichtigkeit Schicht für Schicht bis zur Eingabeschicht weitergibt. Zu den Algorithmen in dieser Kategorie gehören LRP-epsilon, LRP-alphabeta, Deep Taylor, DeepLIFT Rescale, DeepLIFT RevealCancel, DeepShap usw. Der grundlegende Unterschied zwischen verschiedenen Backpropagation-Algorithmen besteht darin, dass sie Schicht für Schicht unterschiedliche Wichtigkeitsausbreitungsregeln verwenden.
3. Okklusionsbasierter Attributionsalgorithmus. Diese Art von Algorithmus leitet die Bedeutung einer Eingabeeinheit basierend auf der Auswirkung des Verdeckens einer Eingabeeinheit auf die Modellausgabe ab. Beispielsweise modelliert der Occlusion-1-Algorithmus (Occlusion-Patch) die Bedeutung des i-ten Pixels (Pixelblocks) als Änderung der Ausgabe, wenn Pixel i nicht verdeckt ist, und verdeckt, wenn andere Pixel nicht verdeckt sind. Der Shapley-Wertalgorithmus berücksichtigt umfassend alle möglichen Verdeckungssituationen anderer Pixel und modelliert die Bedeutung, da sich der Durchschnitt der Ausgabe entsprechend Pixel i unter verschiedenen Verdeckungssituationen ändert. Untersuchungen haben gezeigt, dass der Shapley-Wert der einzige Attributionsalgorithmus ist, der die Axiome Linearität, Dummy, Symmetrie und Effizienz erfüllt.
Nach eingehender Untersuchung verschiedener empirischer Attributionsalgorithmen müssen wir über eine Frage nachdenken: Welches Problem stellt auf mathematischer Ebene die Attribution neuronaler Netze dar? lösen? Gibt es eine einheitliche mathematische Modellierung und ein einheitliches Paradigma hinter vielen empirischen Attributionsalgorithmen? Zu diesem Zweck versuchen wir, die oben genannten Probleme ausgehend von der Definition der Zuschreibung zu berücksichtigen. Die Zuordnung bezieht sich auf die Wichtigkeitsbewertung/den Beitrag jeder Eingabeeinheit zur Ausgabe des neuronalen Netzwerks. Der Schlüssel zur Lösung des oben genannten Problems besteht dann darin, (1) den „Einflussmechanismus der Eingabeeinheit auf die Netzwerkausgabe“ auf mathematischer Ebene zu modellieren und (2) zu erklären, wie viele empirische Attributionsalgorithmen diesen Einflussmechanismus verwenden, um Bedeutung zu entwerfen Attributionsformel.
In Bezug auf den ersten wichtigen Punkt haben unsere Untersuchungen ergeben, dass jede Eingabeeinheit häufig die Ausgabe des neuronalen Netzwerks auf zwei Arten beeinflusst. Einerseits ist eine bestimmte Eingabeeinheit nicht auf andere Eingabeeinheiten angewiesen und kann unabhängig agieren und die Netzwerkausgabe beeinflussen. Diese Art von Einfluss wird als „unabhängiger Effekt“ bezeichnet. Andererseits muss eine Eingabeeinheit mit anderen Eingabeeinheiten zusammenarbeiten, um ein bestimmtes Muster zu bilden, wodurch die Netzwerkausgabe beeinflusst wird. Diese Art von Einfluss wird als „Interaktionseffekt“ bezeichnet. Unsere Theorie beweist, dass die Ausgabe des neuronalen Netzwerks rigoros in die unabhängigen Effekte verschiedener Eingabevariablen sowie die interaktiven Effekte zwischen Eingabevariablen in verschiedenen Mengen zerlegt werden kann.
Unter diesen repräsentiert  den unabhängigen Effekt der i-ten Eingabeeinheit und
den unabhängigen Effekt der i-ten Eingabeeinheit und  repräsentiert den interaktiven Effekt zwischen mehreren Eingabeeinheiten in der Menge S. Für den zweiten Schlüsselpunkt haben wir herausgefunden, dass die internen Mechanismen aller 14 vorhandenen empirischen Attributionsalgorithmen eine Verteilung des oben genannten unabhängigen Nutzens und interaktiven Nutzens darstellen können und dass unterschiedliche Attributionsalgorithmen auf unterschiedlichen Proportionen basieren, um den unabhängigen Nutzen zuzuordnen und interaktiver Nutzen neuronaler Netzwerk-Eingabeeinheiten. Insbesondere soll
repräsentiert den interaktiven Effekt zwischen mehreren Eingabeeinheiten in der Menge S. Für den zweiten Schlüsselpunkt haben wir herausgefunden, dass die internen Mechanismen aller 14 vorhandenen empirischen Attributionsalgorithmen eine Verteilung des oben genannten unabhängigen Nutzens und interaktiven Nutzens darstellen können und dass unterschiedliche Attributionsalgorithmen auf unterschiedlichen Proportionen basieren, um den unabhängigen Nutzen zuzuordnen und interaktiver Nutzen neuronaler Netzwerk-Eingabeeinheiten. Insbesondere soll  den Attributionswert der i-ten Eingabeeinheit darstellen. Wir beweisen rigoros, dass das von allen 14 empirischen Attributionsalgorithmen erhaltene
den Attributionswert der i-ten Eingabeeinheit darstellen. Wir beweisen rigoros, dass das von allen 14 empirischen Attributionsalgorithmen erhaltene  einheitlich als das folgende mathematische Paradigma ausgedrückt werden kann (d. h. die gewichtete Summe aus unabhängigem Nutzen und interaktivem Nutzen):
einheitlich als das folgende mathematische Paradigma ausgedrückt werden kann (d. h. die gewichtete Summe aus unabhängigem Nutzen und interaktivem Nutzen): 
wobei  den Anteil der Zuordnung der unabhängigen Wirkung der j-ten Eingabeeinheit zur i-ten Eingabeeinheit widerspiegelt,
den Anteil der Zuordnung der unabhängigen Wirkung der j-ten Eingabeeinheit zur i-ten Eingabeeinheit widerspiegelt,  die Zuordnung mehrerer Eingabeeinheiten darstellt Der Satz S Der Anteil des Interaktionseffekts zwischen wird der i-ten Eingabeeinheit zugewiesen. Der „grundlegende Unterschied“ zwischen vielen Attributionsalgorithmen besteht darin, dass unterschiedliche Attributionsalgorithmen unterschiedlichen Zuordnungsverhältnissen entsprechen
die Zuordnung mehrerer Eingabeeinheiten darstellt Der Satz S Der Anteil des Interaktionseffekts zwischen wird der i-ten Eingabeeinheit zugewiesen. Der „grundlegende Unterschied“ zwischen vielen Attributionsalgorithmen besteht darin, dass unterschiedliche Attributionsalgorithmen unterschiedlichen Zuordnungsverhältnissen entsprechen  .
.
Tabelle 1 zeigt, wie vierzehn verschiedene Attributionsalgorithmen unabhängige Effekte und interaktive Effekte zuordnen.

Diagramm 1. Die vierzehn Attributionsalgorithmen können alle als mathematisches Paradigma der gewichteten Summe unabhängiger Effekte und interaktiver Effekte geschrieben werden. Unter diesen stellt  den Taylor-unabhängigen Effekt bzw. den Taylor-Interaktionseffekt dar und erfüllt
den Taylor-unabhängigen Effekt bzw. den Taylor-Interaktionseffekt dar und erfüllt
 ist eine Verfeinerung des unabhängigen Effekts
ist eine Verfeinerung des unabhängigen Effekts 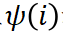 und des interaktiven Effekts
und des interaktiven Effekts  .
.





. 



Bewerten Sie die Zuverlässigkeit des Attributionsalgorithmus Drei Hauptprinzipien 

(1)Kriterium 1: Alle unabhängigen Effekte und interaktiven Effekte im Zuordnungsprozess abdecken. Nachdem wir die Ausgabe des neuronalen Netzwerks in unabhängige Effekte und interaktive Effekte zerlegt haben, sollte ein zuverlässiger Attributionsalgorithmus im Zuordnungsprozess so weit wie möglich alle unabhängigen Effekte und interaktiven Effekte abdecken. Beispielsweise sollte die Zuordnung zum Satz „Ich bin nicht glücklich“ alle unabhängigen Wirkungen der drei Wörter „Ich bin, nicht, glücklich“ abdecken und außerdem J (Ich bin, nicht), J (Ich bin, glücklich) abdecken ), J (nicht glücklich), J (ich bin nicht glücklich) usw. alle möglichen Interaktionseffekte.
(2)Richtlinie 2: Vermeiden Sie es, unabhängige Effekte und Interaktionen irrelevanten Eingabeeinheiten zuzuordnen. Die eigenständige Wirkung der i-ten Eingabeeinheit sollte nur der i-ten Eingabeeinheit und nicht anderen Eingabeeinheiten zugewiesen werden. Ebenso sollte der Interaktionseffekt zwischen Eingabeeinheiten innerhalb der Menge S nur den Eingabeeinheiten innerhalb der Menge S und nicht den Eingabeeinheiten außerhalb der Menge S (die nicht an der Interaktion teilnehmen) zugeordnet werden. Beispielsweise sollte der Interaktionseffekt zwischen „nicht“ und „glücklich“ nicht dem Wort „Ich bin“ zugeordnet werden.
(3)Prinzip Drei: Vollständige Zuordnung. Jeder unabhängige Effekt (Interaktionseffekt) sollte vollständig der entsprechenden Eingabeeinheit zugeordnet sein. Mit anderen Worten: Die von einem bestimmten unabhängigen Effekt (Interaktionseffekt) allen entsprechenden Eingabeeinheiten zugewiesenen Attributionswerte sollten sich genau zu dem Wert des unabhängigen Effekts (Interaktionseffekt) summieren. Beispielsweise würde der Interaktionseffekt J (nicht, glücklich) einen Teil des Effekts  (nicht, glücklich) dem Wort nicht und einen Teil des Effekts
(nicht, glücklich) dem Wort nicht und einen Teil des Effekts  (nicht, glücklich) dem Wort glücklich zuordnen. Dann sollte das Verteilungsverhältnis
(nicht, glücklich) dem Wort glücklich zuordnen. Dann sollte das Verteilungsverhältnis 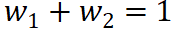 erfüllen.
erfüllen.
Als nächstes haben wir diese drei Bewertungskriterien verwendet, um die oben genannten 14 verschiedenen Attributionsalgorithmen zu bewerten (wie in Tabelle 2 gezeigt). Wir haben festgestellt, dass die Algorithmen „Integrated Gradients“, „Expected Gradients“, „Shapley value“, „Deep Shap“, „DeepLIFT Rescale“ und „DeepLIFT RevealCancel“ alle Zuverlässigkeitskriterien erfüllen.

Tabelle 2. Zusammenfassung, ob 14 verschiedene Attributionsalgorithmen die drei Zuverlässigkeitsbewertungskriterien erfüllen.
Der Autor dieses Artikels, Deng Huiqi, ist Doktor der angewandten Mathematik an der Sun Yat-sen-Universität. Während seiner Doktorarbeit besuchte er die Hong Kong Baptist University Er ist Professor am Department of Computer Science der Texas A&M University und forscht derzeit als Postdoktorand im Team von Professor Zhang Quanshi. Die Forschungsrichtung ist hauptsächlich vertrauenswürdiges/interpretierbares maschinelles Lernen, einschließlich der Erläuterung der Bedeutung der Attribution tiefer neuronaler Netze, der Erklärung der Ausdrucksfähigkeit neuronaler Netze usw.
Deng Huiqi hat in der Anfangsphase viel Arbeit geleistet. Lehrer Zhang half ihr gerade dabei, die Theorie neu zu organisieren, nachdem die ersten Arbeiten abgeschlossen waren, um die Beweismethode und das Beweissystem reibungsloser zu gestalten. Deng Huiqi schrieb vor seinem Abschluss nicht viele Arbeiten, nachdem er Ende 2021 zu Lehrer Zhang kam, und erledigte in mehr als einem Jahr drei Aufgaben im Rahmen des Spielinteraktionssystems, darunter (1) die Entdeckung und theoretische Erklärung des allgemeinen Repräsentationsengpasses neuronaler Systeme Netzwerke, d. h. neuronale Netze, haben sich als noch weniger geeignet für die Modellierung interaktiver Darstellungen mittlerer Komplexität erwiesen. Diese Arbeit hatte das Glück, als mündliche Arbeit des ICLR 2022 ausgewählt zu werden, und ihr Rezensionsergebnis rangierte unter den ersten fünf (Punktzahl 8, 8, 8, 10). (2) Die Theorie beweist den konzeptionellen Darstellungstrend von Bayes'schen Netzwerken und bietet eine neue Perspektive zur Erklärung der Klassifizierungsleistung, der Generalisierungsfähigkeit und der kontroversen Robustheit von Bayes'schen Netzwerken. (3) Erklärt theoretisch die Fähigkeit des neuronalen Netzwerks, während des Trainingsprozesses interaktive Konzepte unterschiedlicher Komplexität zu lernen.
Das obige ist der detaillierte Inhalt vonVerstehen und vereinheitlichen Sie 14 Attributionsalgorithmen, um neuronale Netze interpretierbar zu machen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Algorithmus zum Ersetzen von Seiten
Algorithmus zum Ersetzen von Seiten
 Der Unterschied zwischen Array-Zeiger und Zeiger-Array
Der Unterschied zwischen Array-Zeiger und Zeiger-Array
 C#-Task-Nutzung
C#-Task-Nutzung
 Was tun, wenn Postscript nicht geparst werden kann?
Was tun, wenn Postscript nicht geparst werden kann?
 So erstellen Sie ein rundes Bild in ppt
So erstellen Sie ein rundes Bild in ppt
 Der Unterschied zwischen Header-Dateien und Quelldateien
Der Unterschied zwischen Header-Dateien und Quelldateien
 was der Knoten kann
was der Knoten kann
 So sortieren Sie in Excel
So sortieren Sie in Excel




