
Deep Deterministic Policy Gradient (DDPG) ist ein modellfreier, nicht richtlinienbasierter Tiefenverstärkungsalgorithmus. Er basiert auf Actor-Critic und verwendet den Richtliniengradienten. In diesem Artikel wird Pytorch verwendet Implementieren und Erklären von
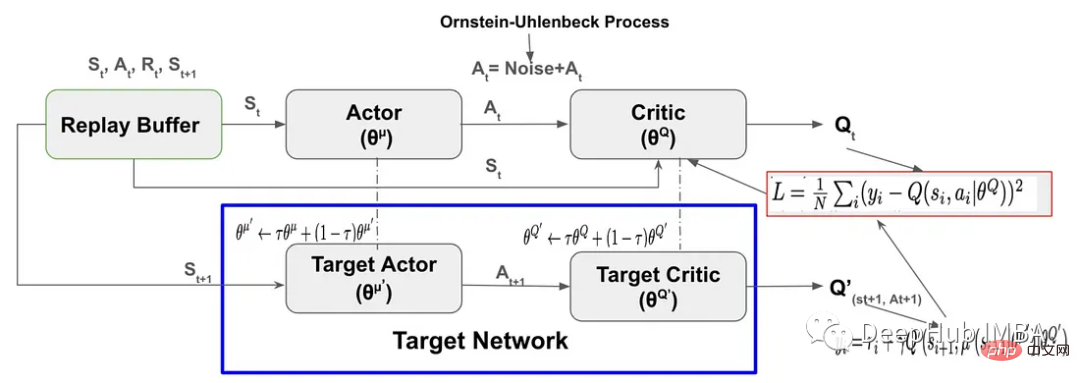
DDPG ist
Wir müssen ein Eins umsetzen Schritt für Schritt:
DDPG verwendet Replay Buffer, um den Prozess und die Belohnungen zu speichern, die durch die Erkundung der Umgebung (Sₜ, aₜ, Rₜ, Sₜ+₁) ermittelt wurden. Der Replay-Puffer spielt eine entscheidende Rolle dabei, dem Agenten dabei zu helfen, das Lernen zu beschleunigen und die Stabilität von DDPG zu gewährleisten:
class Replay_buffer(): ''' Code based on: https://github.com/openai/baselines/blob/master/baselines/deepq/replay_buffer.py Expects tuples of (state, next_state, action, reward, done) ''' def __init__(self, max_size=capacity): """Create Replay buffer. Parameters ---------- size: int Max number of transitions to store in the buffer. When the buffer overflows the old memories are dropped. """ self.storage = [] self.max_size = max_size self.ptr = 0 def push(self, data): if len(self.storage) == self.max_size: self.storage[int(self.ptr)] = data self.ptr = (self.ptr + 1) % self.max_size else: self.storage.append(data) def sample(self, batch_size): """Sample a batch of experiences. Parameters ---------- batch_size: int How many transitions to sample. Returns ------- state: np.array batch of state or observations action: np.array batch of actions executed given a state reward: np.array rewards received as results of executing action next_state: np.array next state next state or observations seen after executing action done: np.array done[i] = 1 if executing ation[i] resulted in the end of an episode and 0 otherwise. """ ind = np.random.randint(0, len(self.storage), size=batch_size) state, next_state, action, reward, done = [], [], [], [], [] for i in ind: st, n_st, act, rew, dn = self.storage[i] state.append(np.array(st, copy=False)) next_state.append(np.array(n_st, copy=False)) action.append(np.array(act, copy=False)) reward.append(np.array(rew, copy=False)) done.append(np.array(dn, copy=False)) return np.array(state), np.array(next_state), np.array(action), np.array(reward).reshape(-1, 1), np.array(done).reshape(-1, 1)
Dies ist eine PyTorch-Implementierung des Actor-Critic Reinforcement Learning-Algorithmus. Dieser Code definiert zwei neuronale Netzwerkmodelle, einen Akteur und einen Kritiker.
Die Eingabe des Akteurmodells: Umgebungszustand; die Ausgabe des Akteurmodells: Aktionen mit kontinuierlichen Werten.
Die Eingabe des Critic-Modells: Umweltzustand und Aktion; die Ausgabe des Critic-Modells: Q-Wert, der die erwartete Gesamtbelohnung des aktuellen Zustands-Aktionspaars ist.
class Actor(nn.Module): """ The Actor model takes in a state observation as input and outputs an action, which is a continuous value. It consists of four fully connected linear layers with ReLU activation functions and a final output layer selects one single optimized action for the state """ def __init__(self, n_states, action_dim, hidden1): super(Actor, self).__init__() self.net = nn.Sequential( nn.Linear(n_states, hidden1), nn.ReLU(), nn.Linear(hidden1, hidden1), nn.ReLU(), nn.Linear(hidden1, hidden1), nn.ReLU(), nn.Linear(hidden1, 1) ) def forward(self, state): return self.net(state) class Critic(nn.Module): """ The Critic model takes in both a state observation and an action as input and outputs a Q-value, which estimates the expected total reward for the current state-action pair. It consists of four linear layers with ReLU activation functions, State and action inputs are concatenated before being fed into the first linear layer. The output layer has a single output, representing the Q-value """ def __init__(self, n_states, action_dim, hidden2): super(Critic, self).__init__() self.net = nn.Sequential( nn.Linear(n_states + action_dim, hidden2), nn.ReLU(), nn.Linear(hidden2, hidden2), nn.ReLU(), nn.Linear(hidden2, hidden2), nn.ReLU(), nn.Linear(hidden2, action_dim) ) def forward(self, state, action): return self.net(torch.cat((state, action), 1))
Das Hinzufügen von Geräuschen zu den von einem Schauspieler ausgewählten Aktionen ist eine Technik, die in DDPG verwendet wird, um die Erkundung zu fördern und den Lernprozess zu verbessern.
Gaußsches Rauschen oder Ornstein-Uhlenbeck-Rauschen können verwendet werden. Gaußsches Rauschen ist einfach und leicht zu implementieren, und Ornstein-Uhlenbeck-Rauschen erzeugt zeitkorreliertes Rauschen, das Agenten dabei helfen kann, den Aktionsraum effizienter zu erkunden. Aber die Fluktuationen des Ornstein-Uhlenbeck-Rauschens sind glatter und weniger zufällig als die Gaußsche Rauschmethode.
import numpy as np import random import copy class OU_Noise(object): """Ornstein-Uhlenbeck process. code from : https://math.stackexchange.com/questions/1287634/implementing-ornstein-uhlenbeck-in-matlab The OU_Noise class has four attributes size: the size of the noise vector to be generated mu: the mean of the noise, set to 0 by default theta: the rate of mean reversion, controlling how quickly the noise returns to the mean sigma: the volatility of the noise, controlling the magnitude of fluctuations """ def __init__(self, size, seed, mu=0., theta=0.15, sigma=0.2): self.mu = mu * np.ones(size) self.theta = theta self.sigma = sigma self.seed = random.seed(seed) self.reset() def reset(self): """Reset the internal state (= noise) to mean (mu).""" self.state = copy.copy(self.mu) def sample(self): """Update internal state and return it as a noise sample. This method uses the current state of the noise and generates the next sample """ dx = self.theta * (self.mu - self.state) + self.sigma * np.array([np.random.normal() for _ in range(len(self.state))]) self.state += dx return self.state
Um Gaußsches Rauschen in DDPG zu verwenden, können Sie Gaußsches Rauschen direkt zum Aktionsauswahlprozess des Agenten hinzufügen.
DDPG (Deep Deterministic Policy Gradient) verwendet zwei Sätze akteurskritischer neuronaler Netze zur Funktionsnäherung. In DDPG ist das Zielnetzwerk Actor-Critic, das dieselbe Struktur und Parametrisierung wie das Actor-Critic-Netzwerk aufweist.
Während des Trainingszeitraums nutzt der Agent sein Actor-Critic-Netzwerk, um mit der Umgebung zu interagieren und speichert Erfahrungstupel (Sₜ, Aₜ, Rₜ, Sₜ+₁) im Replay-Puffer. Der Agent entnimmt dann Stichproben aus dem Replay-Puffer und aktualisiert das Actor-Critic-Netzwerk mit den Daten. Anstatt die Zielnetzwerkgewichte durch direktes Kopieren aus dem Actor-Critic-Netzwerk zu aktualisieren, aktualisiert der DDPG-Algorithmus die Zielnetzwerkgewichte langsam durch einen Prozess, der als Soft-Target-Update bezeichnet wird.
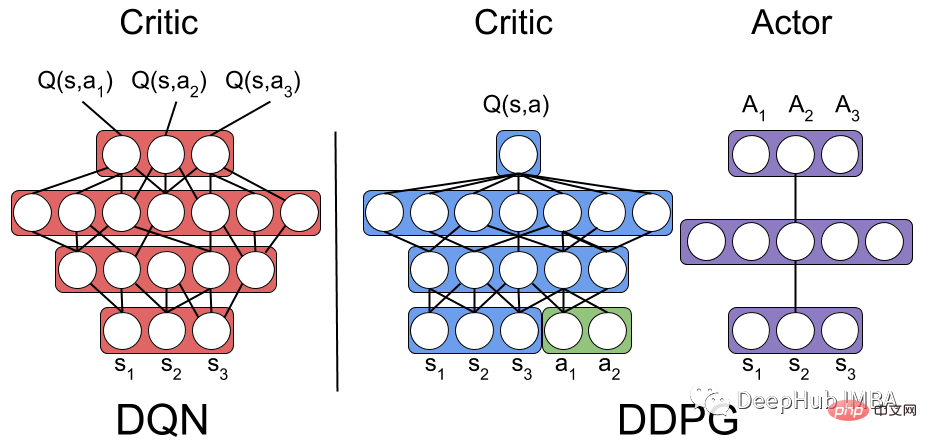
Die Aktualisierung des Soft Targets ist ein Bruchteil der vom Akteur-Kritiker-Netzwerk an das Zielnetzwerk übertragenen Gewichte, die als Zielaktualisierungsrate (τ) bezeichnet wird.
Die Aktualisierungsformel des Soft-Targets lautet wie folgt:
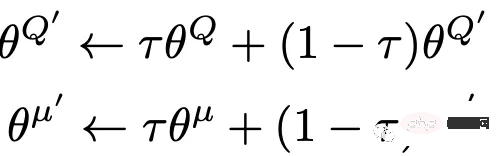
Durch den Einsatz der Soft-Target-Technologie kann die Stabilität des Lernens erheblich verbessert werden.
#Set Hyperparameters # Hyperparameters adapted for performance from capacity=1000000 batch_size=64 update_iteration=200 tau=0.001 # tau for soft updating gamma=0.99 # discount factor directory = './' hidden1=20 # hidden layer for actor hidden2=64. #hiiden laye for critic class DDPG(object): def __init__(self, state_dim, action_dim): """ Initializes the DDPG agent. Takes three arguments: state_dim which is the dimensionality of the state space, action_dim which is the dimensionality of the action space, and max_action which is the maximum value an action can take. Creates a replay buffer, an actor-critic networks and their corresponding target networks. It also initializes the optimizer for both actor and critic networks alog with counters to track the number of training iterations. """ self.replay_buffer = Replay_buffer() self.actor = Actor(state_dim, action_dim, hidden1).to(device) self.actor_target = Actor(state_dim, action_dim,hidden1).to(device) self.actor_target.load_state_dict(self.actor.state_dict()) self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=3e-3) self.critic = Critic(state_dim, action_dim,hidden2).to(device) self.critic_target = Critic(state_dim, action_dim,hidden2).to(device) self.critic_target.load_state_dict(self.critic.state_dict()) self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=2e-2) # learning rate self.num_critic_update_iteration = 0 self.num_actor_update_iteration = 0 self.num_training = 0 def select_action(self, state): """ takes the current state as input and returns an action to take in that state. It uses the actor network to map the state to an action. """ state = torch.FloatTensor(state.reshape(1, -1)).to(device) return self.actor(state).cpu().data.numpy().flatten() def update(self): """ updates the actor and critic networks using a batch of samples from the replay buffer. For each sample in the batch, it computes the target Q value using the target critic network and the target actor network. It then computes the current Q value using the critic network and the action taken by the actor network. It computes the critic loss as the mean squared error between the target Q value and the current Q value, and updates the critic network using gradient descent. It then computes the actor loss as the negative mean Q value using the critic network and the actor network, and updates the actor network using gradient ascent. Finally, it updates the target networks using soft updates, where a small fraction of the actor and critic network weights are transferred to their target counterparts. This process is repeated for a fixed number of iterations. """ for it in range(update_iteration): # For each Sample in replay buffer batch state, next_state, action, reward, done = self.replay_buffer.sample(batch_size) state = torch.FloatTensor(state).to(device) action = torch.FloatTensor(action).to(device) next_state = torch.FloatTensor(next_state).to(device) done = torch.FloatTensor(1-done).to(device) reward = torch.FloatTensor(reward).to(device) # Compute the target Q value target_Q = self.critic_target(next_state, self.actor_target(next_state)) target_Q = reward + (done * gamma * target_Q).detach() # Get current Q estimate current_Q = self.critic(state, action) # Compute critic loss critic_loss = F.mse_loss(current_Q, target_Q) # Optimize the critic self.critic_optimizer.zero_grad() critic_loss.backward() self.critic_optimizer.step() # Compute actor loss as the negative mean Q value using the critic network and the actor network actor_loss = -self.critic(state, self.actor(state)).mean() # Optimize the actor self.actor_optimizer.zero_grad() actor_loss.backward() self.actor_optimizer.step() """ Update the frozen target models using soft updates, where tau,a small fraction of the actor and critic network weights are transferred to their target counterparts. """ for param, target_param in zip(self.critic.parameters(), self.critic_target.parameters()): target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data) for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()): target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data) self.num_actor_update_iteration += 1 self.num_critic_update_iteration += 1 def save(self): """ Saves the state dictionaries of the actor and critic networks to files """ torch.save(self.actor.state_dict(), directory + 'actor.pth') torch.save(self.critic.state_dict(), directory + 'critic.pth') def load(self): """ Loads the state dictionaries of the actor and critic networks to files """ self.actor.load_state_dict(torch.load(directory + 'actor.pth')) self.critic.load_state_dict(torch.load(directory + 'critic.pth'))
Hier verwenden wir „MountainCarContinuous-v0“ von OpenAI Gym, um unser DDPG RL-Modell zu trainieren. Die Umgebung hier bietet kontinuierlichen Aktions- und Beobachtungsraum und das Ziel ist es, das Auto so schnell wie möglich auf den Gipfel des Berges zu bringen wie möglich.
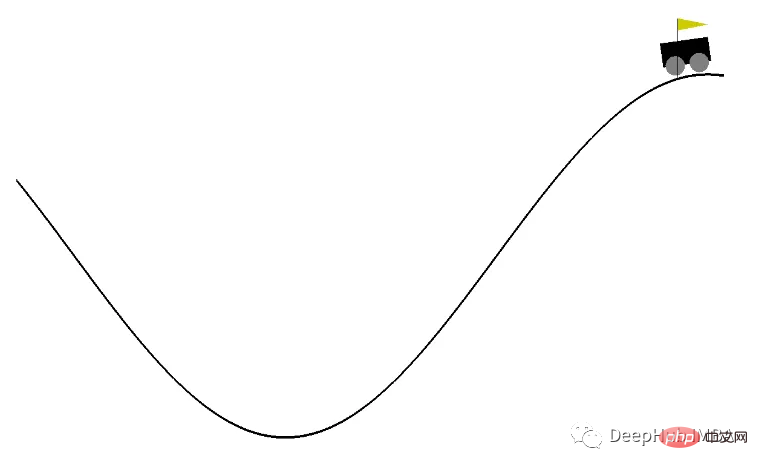
Die verschiedenen Parameter des Algorithmus werden unten definiert, wie z. B. die maximale Anzahl an Trainingszeiten, Erkundungsgeräusch und Aufzeichnungsintervall usw. Durch die Verwendung eines festen Zufallsstartwerts kann der Prozess rückverfolgt werden.
import gym # create the environment env_name='MountainCarContinuous-v0' env = gym.make(env_name) device = 'cuda' if torch.cuda.is_available() else 'cpu' # Define different parameters for training the agent max_episode=100 max_time_steps=5000 ep_r = 0 total_step = 0 score_hist=[] # for rensering the environmnet render=True render_interval=10 # for reproducibility env.seed(0) torch.manual_seed(0) np.random.seed(0) #Environment action ans states state_dim = env.observation_space.shape[0] action_dim = env.action_space.shape[0] max_action = float(env.action_space.high[0]) min_Val = torch.tensor(1e-7).float().to(device) # Exploration Noise exploration_noise=0.1 exploration_noise=0.1 * max_action
Erstellt eine Instanz der DDPG-Agentenklasse, um den Agenten für eine bestimmte Anzahl von Malen zu trainieren. Die update()-Methode des Agenten wird am Ende jeder Runde aufgerufen, um die Parameter zu aktualisieren, und die save()-Methode wird alle zehn Runden verwendet, um die Parameter des Agenten in einer Datei zu speichern.
# Create a DDPG instance
agent = DDPG(state_dim, action_dim)
# Train the agent for max_episodes
for i in range(max_episode):
total_reward = 0
step =0
state = env.reset()
fort in range(max_time_steps):
action = agent.select_action(state)
# Add Gaussian noise to actions for exploration
action = (action + np.random.normal(0, 1, size=action_dim)).clip(-max_action, max_action)
#action += ou_noise.sample()
next_state, reward, done, info = env.step(action)
total_reward += reward
if render and i >= render_interval : env.render()
agent.replay_buffer.push((state, next_state, action, reward, np.float(done)))
state = next_state
if done:
break
step += 1
score_hist.append(total_reward)
total_step += step+1
print("Episode: t{} Total Reward: t{:0.2f}".format( i, total_reward))
agent.update()
if i % 10 == 0:
agent.save()
env.close()test_iteration=100
for i in range(test_iteration):
state = env.reset()
for t in count():
action = agent.select_action(state)
next_state, reward, done, info = env.step(np.float32(action))
ep_r += reward
print(reward)
env.render()
if done:
print("reward{}".format(reward))
print("Episode t{}, the episode reward is t{:0.2f}".format(i, ep_r))
ep_r = 0
env.render()
break
state = next_stateWir verwenden die folgenden Parameter, um das Modell konvergieren zu lassen:
Nach 75 Runden Training Der Effekt ist wie folgt:
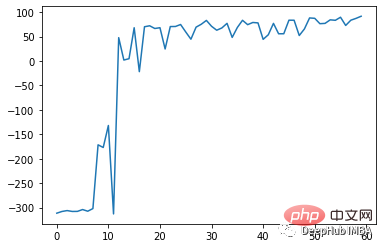
Der DDPG-Algorithmus ist eine von Deep beeinflusste Methode Q-Network Ein modellfreier Off-Policy-Actor-Critic-Algorithmus, inspiriert vom (DQN)-Algorithmus. Es kombiniert die Vorteile von Richtliniengradientenmethoden und Q-Learning, um deterministische Richtlinien in kontinuierlichen Handlungsräumen zu erlernen.
Ähnlich wie DQN verwendet es einen Wiedergabepuffer, um vergangene Erfahrungen und Zielnetzwerke für das Training des Netzwerks zu speichern und dadurch die Stabilität des Trainingsprozesses zu verbessern.
Der DDPG-Algorithmus erfordert eine sorgfältige Hyperparameter-Abstimmung für eine optimale Leistung. Zu den Hyperparametern gehören Lernrate, Stapelgröße, Aktualisierungsrate des Zielnetzwerks und Parameter für Erkennungsrauschen. Kleine Änderungen an Hyperparametern können erhebliche Auswirkungen auf die Leistung des Algorithmus haben.
Das obige ist der detaillierte Inhalt vonPyTorch-Code-Implementierung und Schritt-für-Schritt-Erklärung des DDPG-Verstärkungslernens. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




