
Diese Rezension (Diffusion Models: A Comprehensive Survey of Methods and Applications) stammt von Ming-Hsuan Yang von der University of California und Google Research, dem Cui Bin Laboratory der Peking University sowie CMU, UCLA, Montreal Mila Research und anderen Es ist das erste Mal, dass Forschungsteams eine umfassende Zusammenfassung und Analyse der vorhandenen Diffusionsmodelle durchführen, beginnend mit der detaillierten Klassifizierung des Diffusionsmodellalgorithmus, seiner Verbindung mit anderen fünf großen Generationsmodellen und seiner Anwendung in sieben Hauptbereichen Schließlich wurde das Diffusionsmodell vorgeschlagen.

Artikellink: https://arxiv.org/abs/2209.00796 Zusammenfassung der Papierklassifizierung Github-Link: https://github.com/YangLing0818/Diffusion-Models-Papers-Survey-Taxonomy
Diffusionsmodelle sind die neuen SOTA in tiefen generativen Modellen. Das Diffusionsmodell übertrifft das ursprüngliche SOTA: GAN bei Bilderzeugungsaufgaben und weist in vielen Anwendungsbereichen wie Computer Vision, NLP, Wellenformsignalverarbeitung, multimodaler Modellierung, molekularer Graphenmodellierung und Zeitreihenmodellierung eine hervorragende Leistung auf Reinigung usw. Darüber hinaus stehen Diffusionsmodelle in engem Zusammenhang mit anderen Forschungsfeldern wie Robust Learning, Repräsentationslernen und Reinforcement Learning. Das ursprüngliche Diffusionsmodell weist jedoch auch Mängel auf. Die Stichprobenziehung erfordert normalerweise Tausende von Bewertungsschritten und ist nicht mit der Wahrscheinlichkeitsschätzung vergleichbar, die auf eine Vielzahl von Datentypen angewendet werden kann ist weniger fähig. Heutzutage haben viele Studien große Anstrengungen unternommen, um die oben genannten Einschränkungen aus der Perspektive praktischer Anwendungen zu lösen, oder die Modellfähigkeiten aus theoretischer Sicht analysiert.
Allerdings mangelt es an einer systematischen Überprüfung der jüngsten Fortschritte bei Diffusionsmodellen von Algorithmen bis hin zu Anwendungen. Um den Fortschritt in diesem schnell wachsenden Bereich widerzuspiegeln, präsentieren wir die erste umfassende Übersicht über Diffusionsmodelle. Wir gehen davon aus, dass unsere Arbeit Licht auf die Designüberlegungen und fortschrittlichen Methoden von Diffusionsmodellen werfen, ihre Anwendungen in verschiedenen Bereichen demonstrieren und zukünftige Forschungsrichtungen aufzeigen wird. Die Zusammenfassung dieser Rezension ist unten dargestellt:
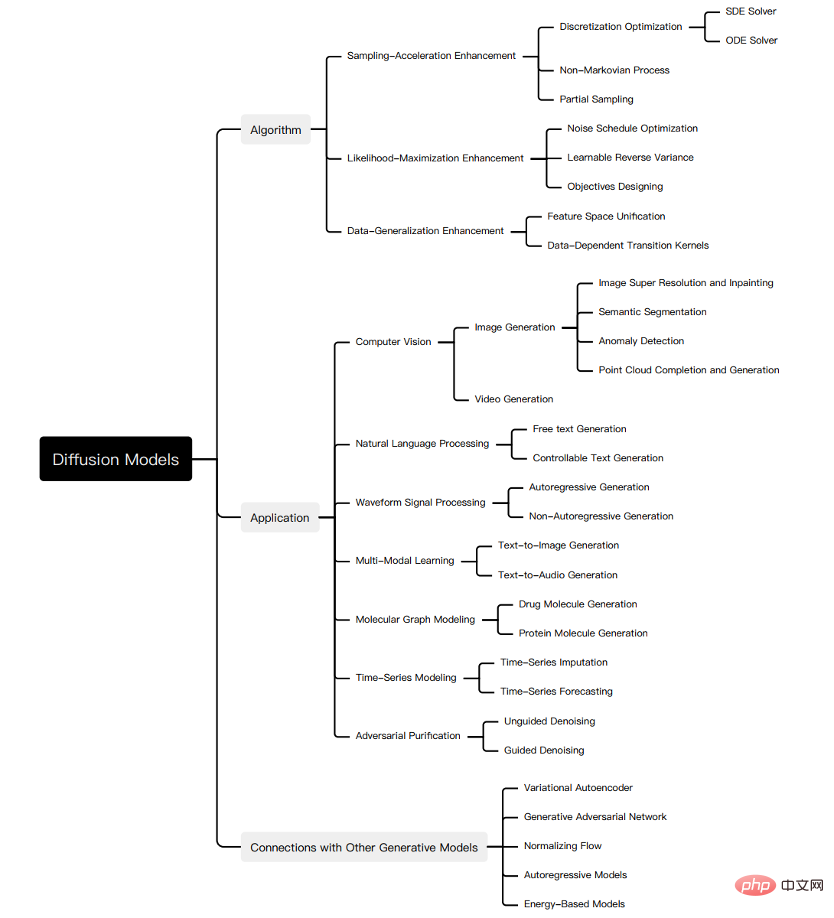
Obwohl das Diffusionsmodell bei verschiedenen Aufgaben eine hervorragende Leistung aufweist, weist es immer noch seine eigenen Mängel auf, und es wurden viele Studien zum Diffusionsmodell durchgeführt gemacht. Um den Forschungsfortschritt von Diffusionsmodellen systematisch zu klären, haben wir die drei Hauptmängel des ursprünglichen Diffusionsmodells zusammengefasst: langsame Abtastgeschwindigkeit, schlechte Maximierungswahrscheinlichkeit und schwache Fähigkeit zur Datenverallgemeinerung, und vorgeschlagen, die Verbesserungsforschung zu Diffusionsmodellen entsprechend zu unterteilen Drei Kategorien: Verbesserung der Abtastgeschwindigkeit, Verbesserung der maximalen Wahrscheinlichkeit und Verbesserung der Datengeneralisierung. Wir erläutern zunächst die Motivation zur Verbesserung und klassifizieren dann die Forschung in jede Verbesserungsrichtung entsprechend den Merkmalen der Methode weiter, um die Zusammenhänge und Unterschiede zwischen den Methoden klar aufzuzeigen. Hier werden nur einige wichtige Methoden als Beispiele ausgewählt, wie in der Abbildung gezeigt:
Nach der Analyse der drei Arten von Diffusionsmodellen stellen wir die anderen fünf vor generative Modelle GAN, VAE, autoregressives Modell, normalisierender Fluss und energiebasiertes Modell. Angesichts der hervorragenden Eigenschaften des Diffusionsmodells haben Forscher das Diffusionsmodell auf der Grundlage seiner Eigenschaften mit anderen generativen Modellen kombiniert. Um die Eigenschaften und Verbesserungen des Diffusionsmodells weiter zu demonstrieren, haben wir daher die Kombination des Diffusionsmodells im Detail vorgestellt und andere generative Modelle funktionieren und veranschaulichen Verbesserungen gegenüber dem ursprünglichen generativen Modell. Das Diffusionsmodell weist in vielen Bereichen eine hervorragende Leistung auf. Angesichts der Tatsache, dass das Diffusionsmodell bei Anwendungen in verschiedenen Bereichen unterschiedliche Verformungen aufweist, haben wir systematisch die Anwendungsforschung des Diffusionsmodells eingeführt, einschließlich der folgenden Bereiche: Computer Vision, NLP, Wellenformsignalverarbeitung, multimodale Modellierung, Modellierung molekularer Graphen, Zeitreihenmodellierung, kontradiktorische Reinigung.
Für jede Aufgabe definieren wir die Aufgabe und führen die Arbeit mithilfe eines Diffusionsmodells ein, um die Aufgabe zu bewältigen. Wir fassen die Hauptbeiträge dieser Arbeit wie folgt zusammen:
#🎜 🎜##🎜 🎜#
Dies zeigt, dass die Vorwärtskette ein Markov-Prozess ist, x_t die Stichprobe nach dem Hinzufügen von T-Schritt-Rauschen ist und β_t der Parameter ist, der den Fortschritt des angegebenen Rauschens steuert Vorauszahlung. Wenn gegen 1 tendiert, kann davon ausgegangen werden, dass x_T näherungsweise der Standard-Gauß-Verteilung folgt. Wenn β_t klein ist, kann der Übertragungskern des umgekehrten Prozesses ungefähr als Gaußsch betrachtet werden: Ändern Sie die Variation. Die Untergrenze wird als Verlustfunktion gelernt:
# B.Score-Based Generative Modelle (SGM)# 🎜🎜#
B.Score-Based Generative Modelle (SGM)# 🎜🎜#
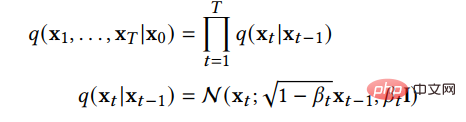
 # 🎜🎜 # und eine entsprechende inverse SDE, um die vorherige Verteilung zurück in die ursprüngliche Datenverteilung umzuwandeln:
# 🎜🎜 # und eine entsprechende inverse SDE, um die vorherige Verteilung zurück in die ursprüngliche Datenverteilung umzuwandeln:
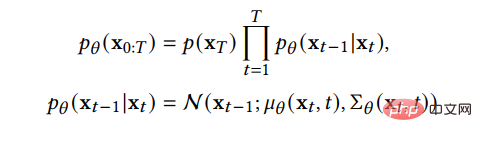
Um den Diffusionsprozess umzukehren und Daten zu generieren, benötigen wir also nur die Bruchfunktion zu jedem Zeitpunkt. Mithilfe der Score-Matching-Technik können wir die Score-Funktion durch die folgende Verlustfunktion lernen:
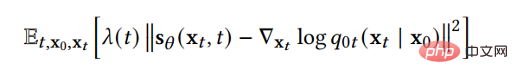
Eine weitere Einführung in die beiden Methoden und die Beziehung zwischen beiden finden Sie in unserem Artikel.
Die drei Hauptnachteile des ursprünglichen Diffusionsmodells sind langsame Abtastgeschwindigkeit, maximale Wahrscheinlichkeitsdifferenz und schwache Fähigkeit zur Datenverallgemeinerung. Viele neuere Studien haben sich mit diesen Mängeln befasst, daher klassifizieren wir verbesserte Diffusionsmodelle in drei Kategorien: Verbesserung der Abtastgeschwindigkeit, Verbesserung der maximalen Wahrscheinlichkeit und Verbesserung der Datenverallgemeinerung. In den nächsten drei, vier und fünf Abschnitten werden wir diese drei Modelltypen im Detail vorstellen.
Um die Qualität der neuen Probe zu optimieren, erfordert das Diffusionsmodell bei seiner Anwendung oft Tausende von Berechnungsschritten, um eine neue Probe zu erhalten. Dies schränkt den praktischen Anwendungswert des Diffusionsmodells ein, da wir in der tatsächlichen Anwendung häufig eine große Anzahl neuer Proben generieren müssen, um Materialien für den nächsten Verarbeitungsschritt bereitzustellen. Forscher haben umfangreiche Untersuchungen zur Verbesserung der Abtastgeschwindigkeit des Diffusionsmodells durchgeführt. Wir beschreiben diese Studien im Detail. Wir verfeinern es in drei Methoden: Diskretisierungsoptimierung, Nicht-Markovian-Prozess und Teilabtastung.
A. Methode zur Diskretisierungsoptimierung Optimieren Sie die Methode zur Lösung von Diffusions-SDE. Da bei der Lösung komplexer SDE in der Realität nur diskrete Lösungen zur Annäherung an die reale Lösung verwendet werden können, versucht diese Art von Methode, die Diskretisierungsmethode von SDE zu optimieren, um die Anzahl diskreter Schritte zu reduzieren und gleichzeitig die Probenqualität sicherzustellen. SGM schlägt eine allgemeine Methode zur Lösung des Rückwärtsprozesses vor, d. h. die gleiche Diskretisierungsmethode wird für den Vorwärts- und Rückwärtsprozess angewendet. Wenn die Vorwärts-SDE eine Diskretisierung erhält:
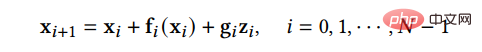
, dann können wir die inverse SDE auf die gleiche Weise diskretisieren:
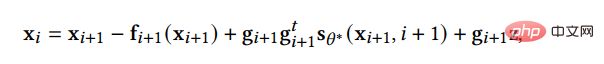
Diese Methode ist etwas besser als das naive DDPM. Darüber hinaus fügt SGM dem SDE-Löser einen Korrektor hinzu, sodass die bei jedem Schritt generierten Stichproben die richtige Verteilung aufweisen. Bei jedem Schritt der Lösung, nachdem dem Löser eine Stichprobe gegeben wurde, verwendet der Geraderichter eine Markov-Ketten-Monte-Carlo-Methode, um die Verteilung der gerade generierten Stichprobe zu glätten. Experimente zeigen, dass das Hinzufügen eines Korrektors zum Löser effizienter ist, als die Anzahl der Schritte im Löser direkt zu erhöhen.
B.Nicht-Markovian-Prozess Die Methode durchbricht die Einschränkungen des ursprünglichen Markovian-Prozesses und kann auf mehr vergangene Proben zurückgreifen, um neue Proben vorherzusagen länger Selbst bei großen Zeiten können bessere Vorhersagen getroffen werden, wodurch der Probenahmeprozess beschleunigt wird. Unter diesen geht das Hauptwerk DDIM nicht mehr davon aus, dass der Vorwärtsprozess ein Markov-Prozess ist, sondern folgt der folgenden Verteilung:
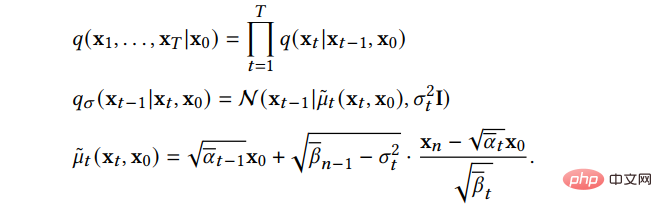
Der Abtastprozess von DDIM kann als diskretisierte göttliche reguläre Differentialgleichung betrachtet werden Der Sampling-Prozess ist effizienter und unterstützt die Sample-Interpolation. Weitere Untersuchungen ergaben, dass DDIM als Sonderfall des On-Manifold-Diffusionsmodells PNDM angesehen werden kann.
C. Partial Sampling Die Sampling-Zeit wird direkt reduziert, indem ein Teil der Zeitknoten im Generierungsprozess ignoriert und nur die verbleibenden Zeitknoten zum Generieren von Samples verwendet werden. Beispielsweise destilliert die progressive Destillation ein effizienteres Diffusionsmodell aus einem trainierten Diffusionsmodell. Für ein trainiertes Diffusionsmodell trainiert Progressive Distillation ein Diffusionsmodell neu, sodass ein Schritt des neuen Diffusionsmodells den beiden Schritten des trainierten Diffusionsmodells entspricht, sodass das neue Modell die Hälfte des Probenahmeprozesses des alten Modells einsparen kann. Der spezifische Algorithmus lautet wie folgt:

Ein kontinuierlicher Zyklus dieses Destillationsprozesses kann die Probenahmeschritte exponentiell reduzieren.
Die Leistung des Diffusionsmodells bei der Maximum-Likelihood-Schätzung ist schlechter als die des auf der Likelihood-Funktion basierenden Generierungsmodells, aber die Maximum-Likelihood-Schätzung ist in vielen Anwendungsszenarien wie der Bildkomprimierung von großer Bedeutung , halbüberwachtes Lernen, kontradiktorische Reinigung. Da es schwierig ist, die Log-Likelihood direkt zu berechnen, konzentriert sich die Forschung hauptsächlich auf die Optimierung und Analyse der Variationsuntergrenzen (VLB). Wir arbeiten an Modellen, die die Maximum-Likelihood-Schätzungen von Diffusionsmodellen verbessern. Wir verfeinern es in drei Kategorien von Methoden: Zielentwurf, Lärmplanungsoptimierung und erlernbare umgekehrte Varianz. Die Methode
A.Objectives Design verwendet Diffusions-SDE, um die Beziehung zwischen der Log-Likelihood der generierten Daten und der Verlustfunktion des Score-Funktions-Matchings abzuleiten. Auf diese Weise können durch geeignete Gestaltung der Verlustfunktion VLB und Log-Likelihood maximiert werden. Song et al. haben bewiesen, dass die Gewichtsfunktion der Verlustfunktion so gestaltet werden kann, dass der Wahrscheinlichkeitsfunktionswert der durch Plug-in-Reverse-SDE erzeugten Stichprobe kleiner oder gleich dem Verlustfunktionswert ist, d. h. die Verlustfunktion die Obergrenze der Wahrscheinlichkeitsfunktion. Die Verlustfunktion für die Teilfunktionsanpassung lautet wie folgt:
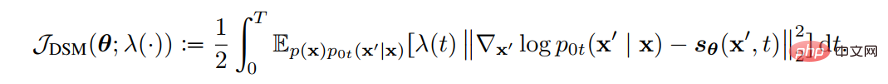
Wir müssen nur die Gewichtsfunktion λ (t) auf den Diffusionskoeffizienten g (t) setzen, damit die Verlustfunktion zum VLB der Likelihood-Funktion wird , das heißt:
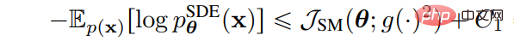
B.Noise Schedule Optimization Erhöhen Sie den VLB, indem Sie den Lärmplan des Vorwärtsprozesses entwerfen oder lernen. VDM beweist, dass die Verlustfunktion vollständig durch den Endpunkt der Signal-Rausch-Verhältnis-Funktion SNR(t) bestimmt wird, wenn sich die diskreten Schritte der Unendlichkeit nähern:
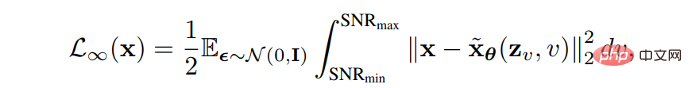
Die Funktion des Signal-Rausch-Verhältnisses kann gelernt werden, indem der Endpunkt von SNR(t) VLB optimiert wird, und andere Aspekte des Modells werden durch Lernen des Funktionswerts im mittleren Teil der Signal-Rausch-Verhältnis-Funktion verbessert. Die
C.Learnable Reverse Variance -Methode lernt die Varianz des umgekehrten Prozesses, reduziert dadurch Anpassungsfehler und kann VLB effektiv maximieren. Analytic-DPM beweist, dass es im umgekehrten Prozess in DDPM und DDIM eine optimale Erwartung und Varianz gibt:

Unter Verwendung der obigen Formel und der trainierten Score-Funktion wird unter den Bedingungen des gegebenen Vorwärtsprozesses die optimale Ausgezeichnet VLB kann annähernd erreicht werden.
Das Diffusionsmodell geht davon aus, dass die Daten im euklidischen Raum existieren, also in einer Mannigfaltigkeit mit planarer Geometrie, und das Hinzufügen von Gauß'schem Rauschen wird die Daten unweigerlich in einen kontinuierlichen Zustandsraum umwandeln, so das Diffusionsmodell Zunächst können nur kontinuierliche Daten wie Bilder verarbeitet werden, und die direkte Anwendung diskreter Daten oder anderer Datentypen hat nur geringe Auswirkungen. Dies schränkt die Anwendungsszenarien des Diffusionsmodells ein. Mehrere Forschungsarbeiten verallgemeinern das Diffusionsmodell auf andere Datentypen, und wir veranschaulichen diese Methoden im Detail. Wir klassifizieren es in zwei Arten von Methoden: Feature Space Unification und Data-Dependent Transition Kernels. Die Methode „A.Feature Space Unification“ wandelt die Daten in einen einheitlichen latenten Raum um und verteilt sie dann auf dem latenten Raum. LSGM schlägt vor, die Daten über das VAE-Framework in einen kontinuierlichen latenten Raum umzuwandeln und sie dann darauf zu verteilen. Die Schwierigkeit dieser Methode besteht darin, VAE und Diffusionsmodell gleichzeitig zu trainieren. LSGM zeigt, dass der fraktionelle Matching-Verlust nicht mehr gilt, da der zugrunde liegende Prior unlösbar ist. LSGM verwendet direkt die traditionelle Verlustfunktion ELBO in VAE als Verlustfunktion und leitet die Beziehung zwischen ELBO und Score-Matching ab:
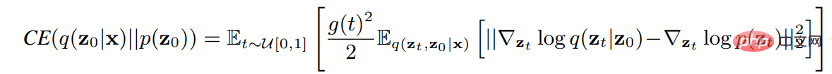
Diese Formel gilt, wenn Konstanten ignoriert werden. Durch Parametrisieren der Bruchfunktion der Probe im Diffusionsprozess kann LSGM ELBO effizient lernen und optimieren. Die Methode
B.Data-Dependent Transition Kernels entwirft die Übergangskerne im Diffusionsprozess entsprechend den Merkmalen des Datentyps, sodass das Diffusionsmodell direkt auf bestimmte Datentypen angewendet werden kann. D3PM hat einen Übergangskernel für diskrete Daten entwickelt, der auf Lazy Random Walk, Absorbing State usw. eingestellt werden kann. GEODIFF entwarf ein translatorisch-rotationsinvariantes graphisches neuronales Netzwerk für 3D-Molekülgraphendaten und bewies, dass die invariante Anfangsverteilung und der Übergangskern eine invariante Randverteilung ableiten können. Angenommen, T ist eine Translations-Rotations-Transformation, wie zum Beispiel:
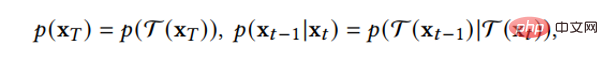
Dann hat die generierte Stichprobenverteilung auch Translations-Rotations-Invarianz:
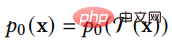
und die Verbindung mit anderen generativen Modellen in jedem von ihnen Im folgenden Abschnitt stellen wir zunächst fünf weitere wichtige Kategorien generativer Modelle vor und analysieren deren Vorteile und Einschränkungen. Anschließend stellen wir vor, wie Diffusionsmodelle damit zusammenhängen und veranschaulichen, wie diese generativen Modelle durch die Einbeziehung von Diffusionsmodellen verbessert werden können. Die Beziehung zwischen VAE, GAN, autoregressivem Modell, normalisierendem Fluss, energiebasiertem Modell und Diffusionsmodell ist in der folgenden Abbildung dargestellt: (DDPM kann als hierarchisches Markovian VAE betrachtet werden.) Es gibt aber auch Unterschiede zwischen DDPM und allgemeiner VAE. Als VAE befolgen sowohl der Encoder als auch der Decoder von DDPM die Gaußsche Verteilung und verfügen über Markov-Zeilen;
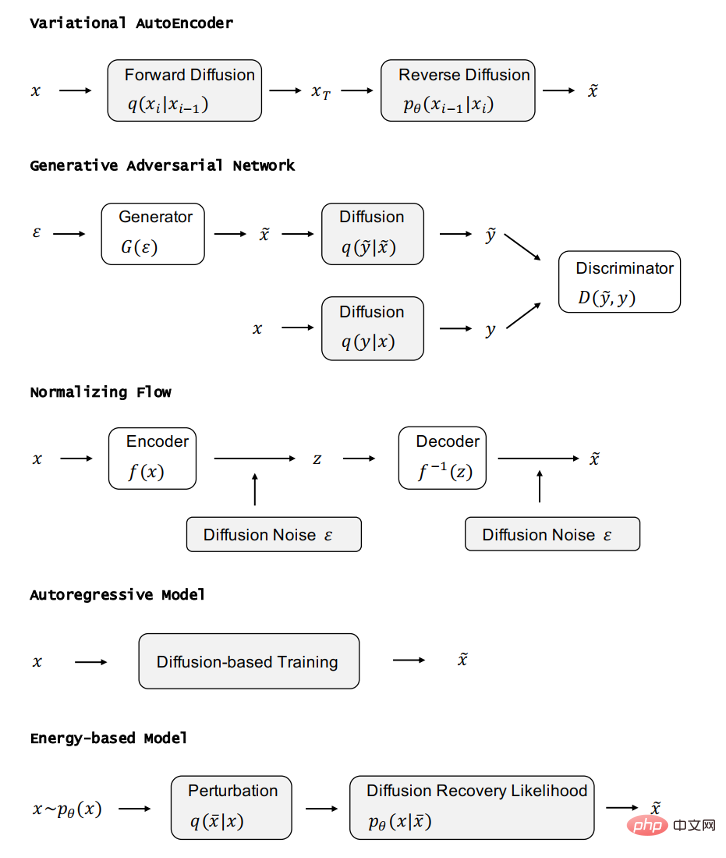 DDPM kann GAN dabei helfen, das Problem des instabilen Trainings zu lösen. Da sich die Daten in einer niedrigdimensionalen Mannigfaltigkeit in einem hochdimensionalen Raum befinden, weist die Verteilung der von GAN generierten Daten eine geringe Überlappung mit der Verteilung der realen Daten auf, was zu einem instabilen Training führt. Das Diffusionsmodell bietet einen Prozess zum systematischen Hinzufügen von Rauschen zu den generierten Daten und den realen Daten und sendet dann die mit Rauschen hinzugefügten Daten an den Diskriminator. Dadurch kann das Problem, dass GAN nicht trainiert werden kann, effektiv gelöst werden und das Training ist instabil.
DDPM kann GAN dabei helfen, das Problem des instabilen Trainings zu lösen. Da sich die Daten in einer niedrigdimensionalen Mannigfaltigkeit in einem hochdimensionalen Raum befinden, weist die Verteilung der von GAN generierten Daten eine geringe Überlappung mit der Verteilung der realen Daten auf, was zu einem instabilen Training führt. Das Diffusionsmodell bietet einen Prozess zum systematischen Hinzufügen von Rauschen zu den generierten Daten und den realen Daten und sendet dann die mit Rauschen hinzugefügten Daten an den Diskriminator. Dadurch kann das Problem, dass GAN nicht trainiert werden kann, effektiv gelöst werden und das Training ist instabil.
Der normalisierende Fluss wandelt die Daten über eine Bijektionsfunktion in eine vorherige Verteilung um. Dieser Ansatz schränkt die Ausdrucksfähigkeit des normalisierenden Flusses ein, was zu schlechten Anwendungsergebnissen führt. Das analoge Diffusionsmodell fügt dem Encoder Rauschen hinzu, was die Ausdrucksfähigkeit des Normalisierungsflusses erhöhen kann. Aus einer anderen Perspektive besteht dieser Ansatz darin, das Diffusionsmodell auf ein Modell zu erweitern, das auch im Vorwärtsprozess gelernt werden kann.
Sie können das Diffusionsmodell verwenden, um in multimodalen Aufgaben (GLIDE) Text in Bilder zu generieren:

Sie können das Diffusionsmodell auch verwenden, um Arzneimittelmoleküle und Proteinmoleküle bei der Generierung molekularer Diagramme (GeoDiff) zu generieren. :
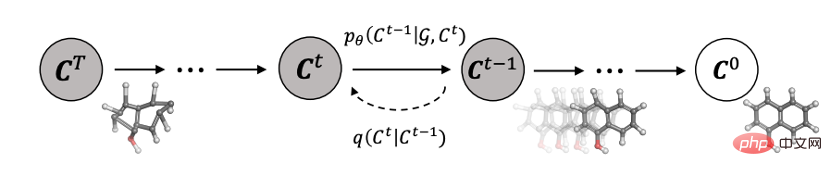
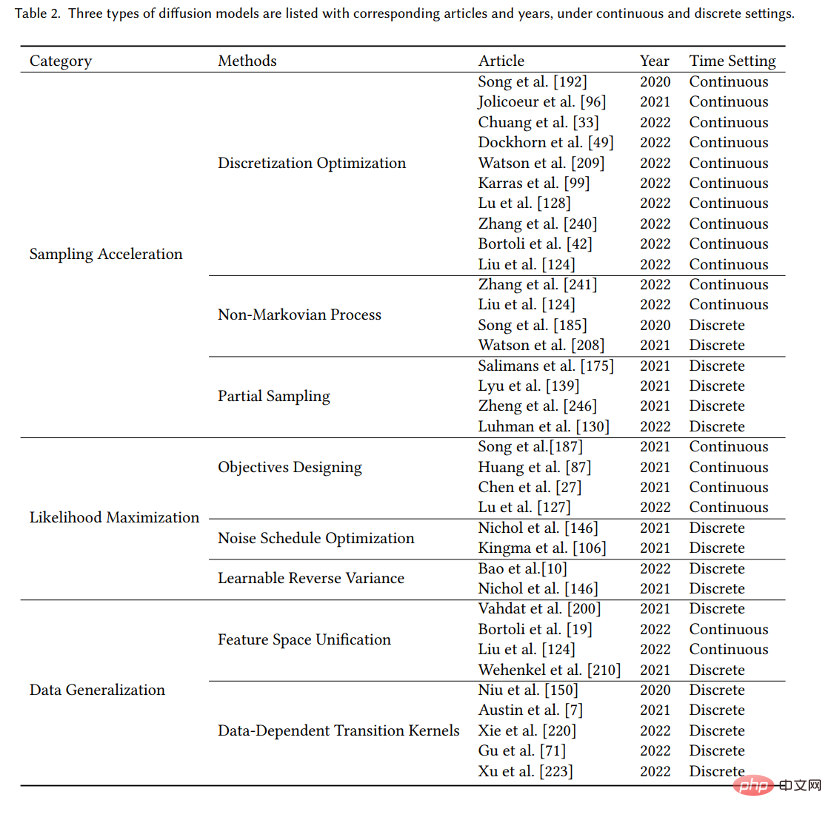
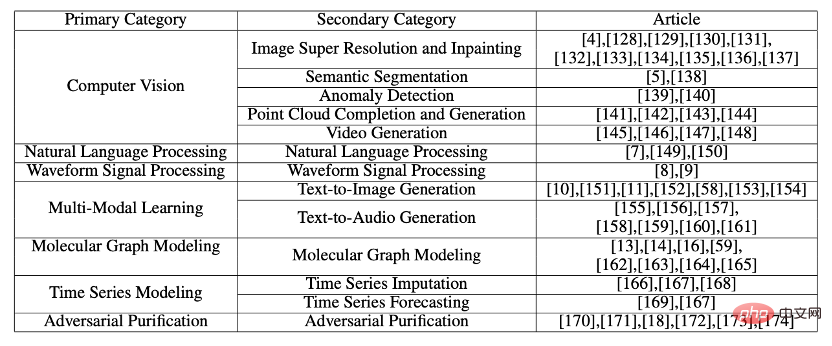
Die Zusammenfassung der Anwendungsklassifizierung ist in der Tabelle dargestellt:
Das obige ist der detaillierte Inhalt vonDas Diffusionsmodell explodiert. Dies ist die erste Überprüfung und Zusammenfassung von Github-Artikeln. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




