mysql索引为什么快

索引就是通过事先排好序，从而在查找时可以应用二分查找等高效率的算法。一般的顺序查找，复杂度为O(n)，而二分查找复杂度为O(log2n)；当n很大时，二者的效率相差及其悬殊。

本教程操作环境：windows7系统、mysql8版本、Dell G3电脑。

Mysql 作为互联网中非常热门的数据库，其底层的存储引擎和数据检索引擎的设计非常重要，尤其是 Mysql 数据的存储形式以及索引的设计，决定了 Mysql 整体的数据检索性能。

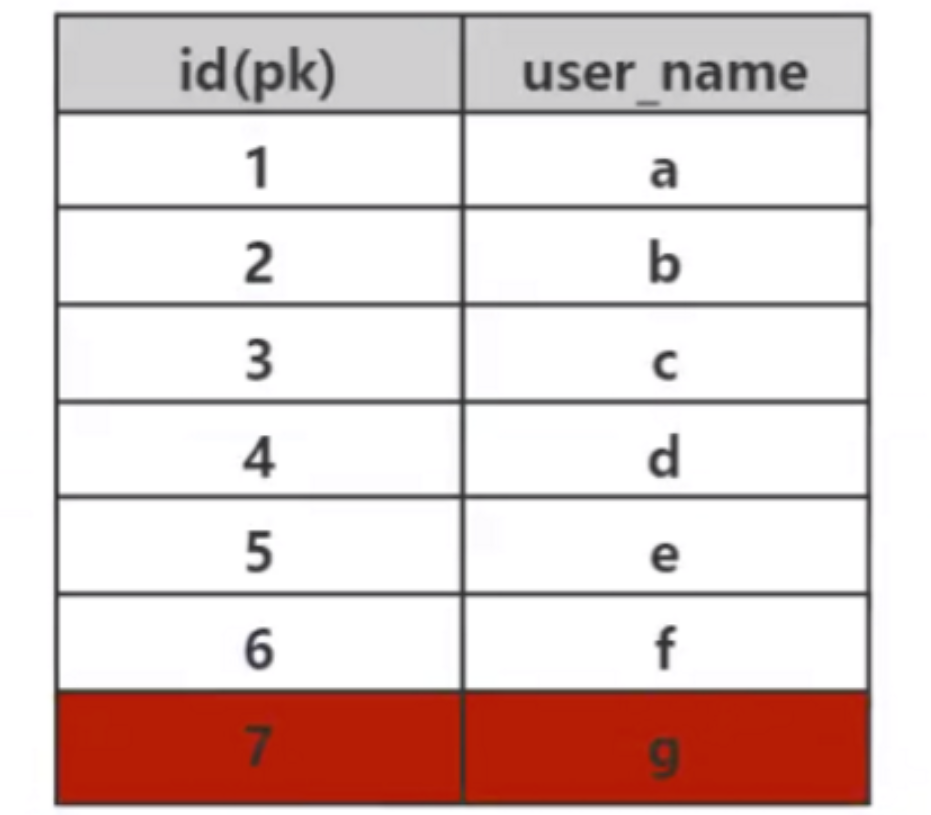
我们知道，索引的作用是做数据的快速检索，而快速检索的实现的本质是数据结构。通过不同数据结构的选择，实现各种数据快速检索。在数据库中，高效的查找算法是非常重要的，因为数据库中存储了大量数据，一个高效的索引能节省巨大的时间。比如下面这个数据表，如果 Mysql 没有实现索引算法，那么查找 id=7 这个数据，那么只能采取暴力顺序遍历查找，找到 id=7 这个数据需要比较 7 次，如果这个表存储的是 1000W 个数据，查找 id=1000W 这个数据那就要比较 1000W 次，这种速度是不能接受的。

一、Mysql 索引底层数据结构选型

哈希表（Hash）

哈希表是做数据快速检索的有效利器。

哈希算法：也叫散列算法，就是把任意值(key)通过哈希函数变换为固定长度的 key 地址，通过这个地址进行具体数据的数据结构。

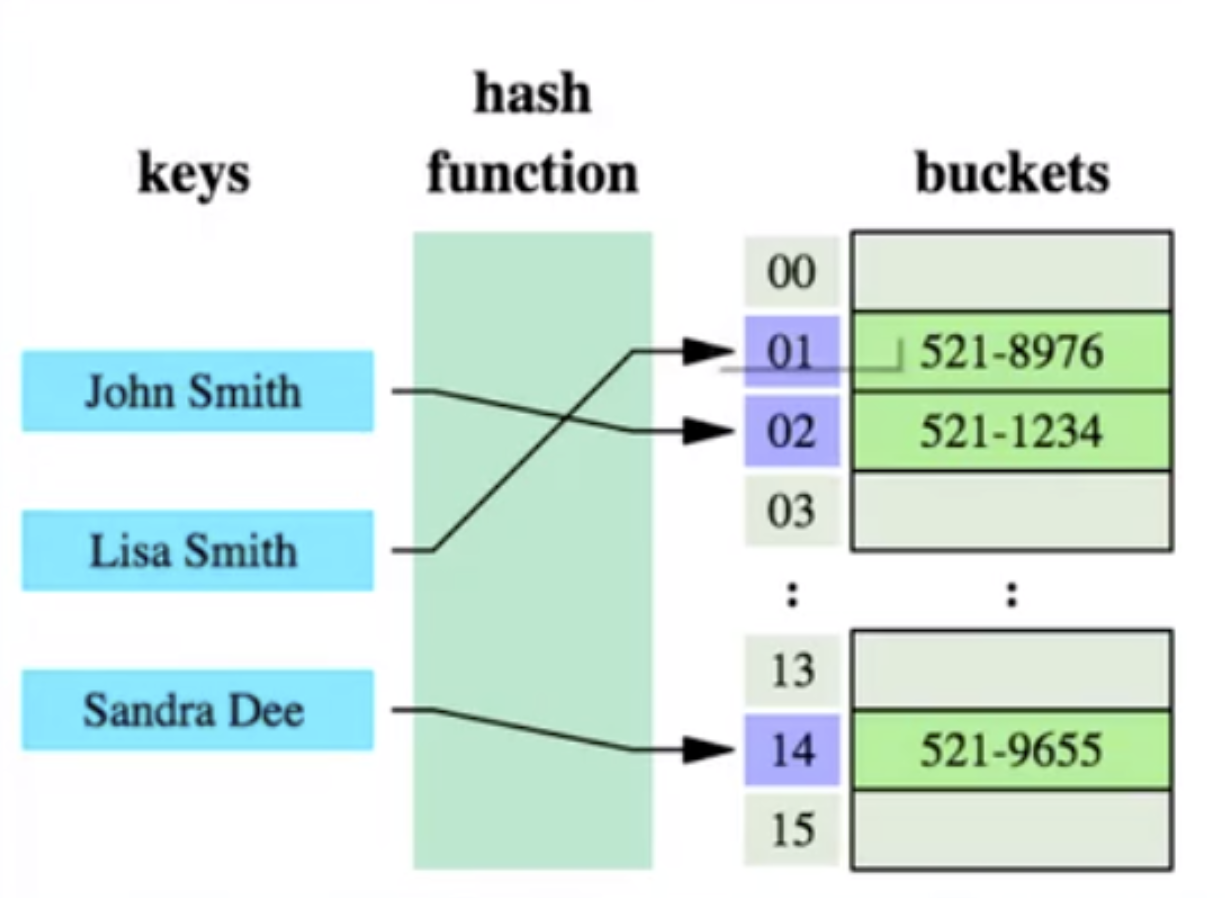
考虑这个数据库表 user，表中一共有 7 个数据，我们需要检索 id=7 的数据，SQL 语法是：

select * from user where id=7;

哈希算法首先计算存储 id=7 的数据的物理地址 addr=hash(7)=4231，而 4231 映射的物理地址是 0x77，0x77 就是 id=7 存储的额数据的物理地址，通过该独立地址可以找到对应 user_name='g'这个数据。这就是哈希算法快速检索数据的计算过程。

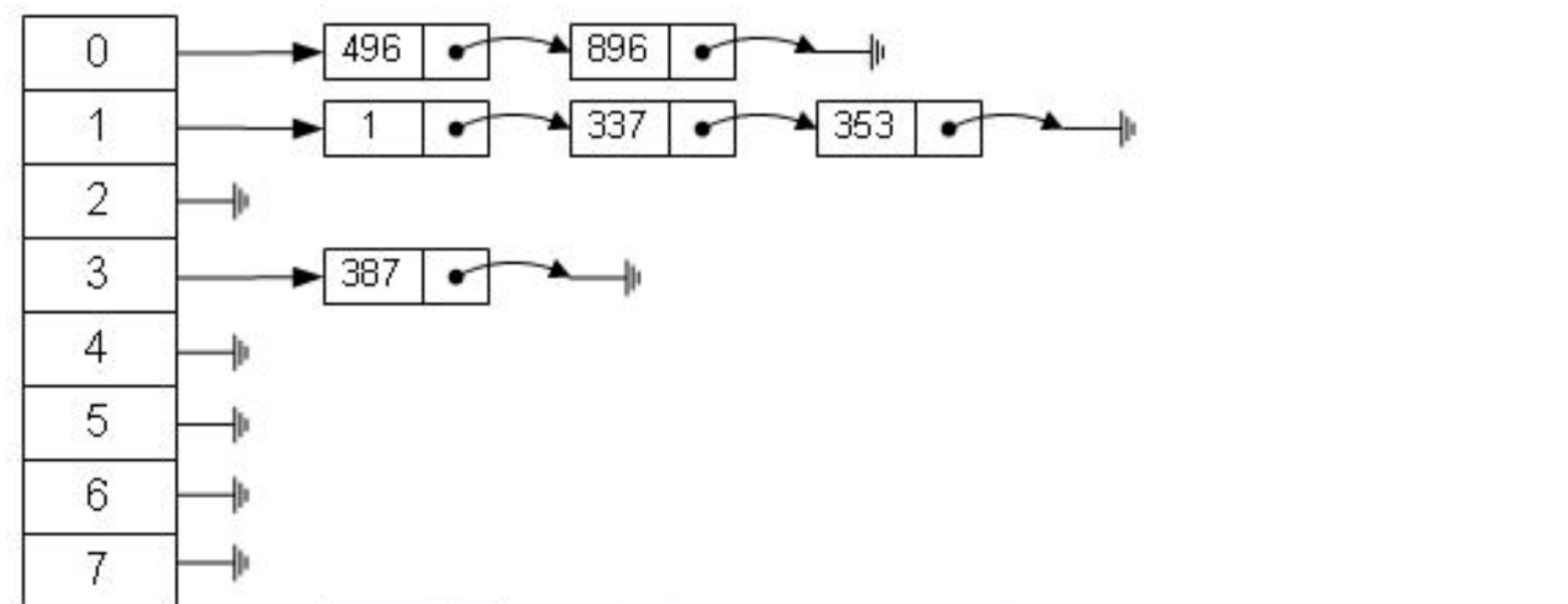
但是哈希算法有个数据碰撞的问题，也就是哈希函数可能对不同的 key 会计算出同一个结果，比如 hash(7)可能跟 hash(199)计算出来的结果一样，也就是不同的 key 映射到同一个结果了，这就是碰撞问题。解决碰撞问题的一个常见处理方式就是链地址法，即用链表把碰撞的数据接连起来。计算哈希值之后，还需要检查该哈希值是否存在碰撞数据链表，有则一直遍历到链表尾，直达找到真正的 key 对应的数据为止。

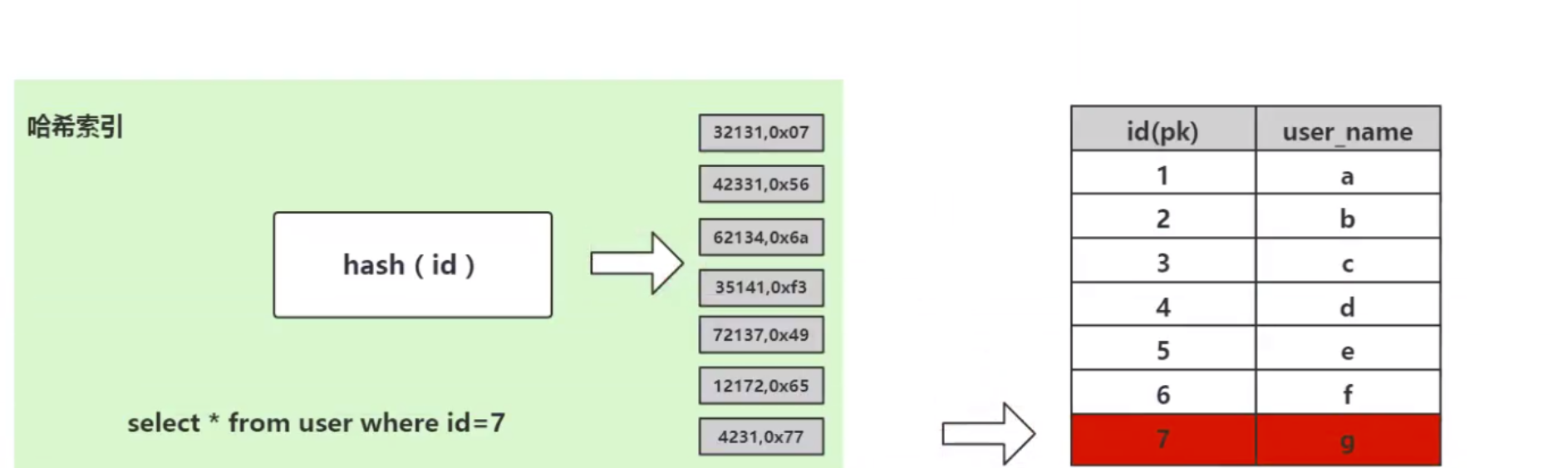
从算法时间复杂度分析来看，哈希算法时间复杂度为 O（1），检索速度非常快。比如查找 id=7 的数据，哈希索引只需要计算一次就可以获取到对应的数据，检索速度非常快。但是 Mysql 并没有采取哈希作为其底层算法，这是为什么呢？

因为考虑到数据检索有一个常用手段就是范围查找，比如以下这个 SQL 语句：

select * from user where id \>3;

针对以上这个语句，我们希望做的是找出 id>3 的数据，这是很典型的范围查找。如果使用哈希算法实现的索引，范围查找怎么做呢？一个简单的思路就是一次把所有数据找出来加载到内存，然后再在内存里筛选筛选目标范围内的数据。但是这个范围查找的方法也太笨重了，没有一点效率而言。

所以，使用哈希算法实现的索引虽然可以做到快速检索数据，但是没办法做数据高效范围查找，因此哈希索引是不适合作为 Mysql 的底层索引的数据结构。

二叉查找树(BST)

二叉查找树是一种支持数据快速查找的数据结构，如图下所示:

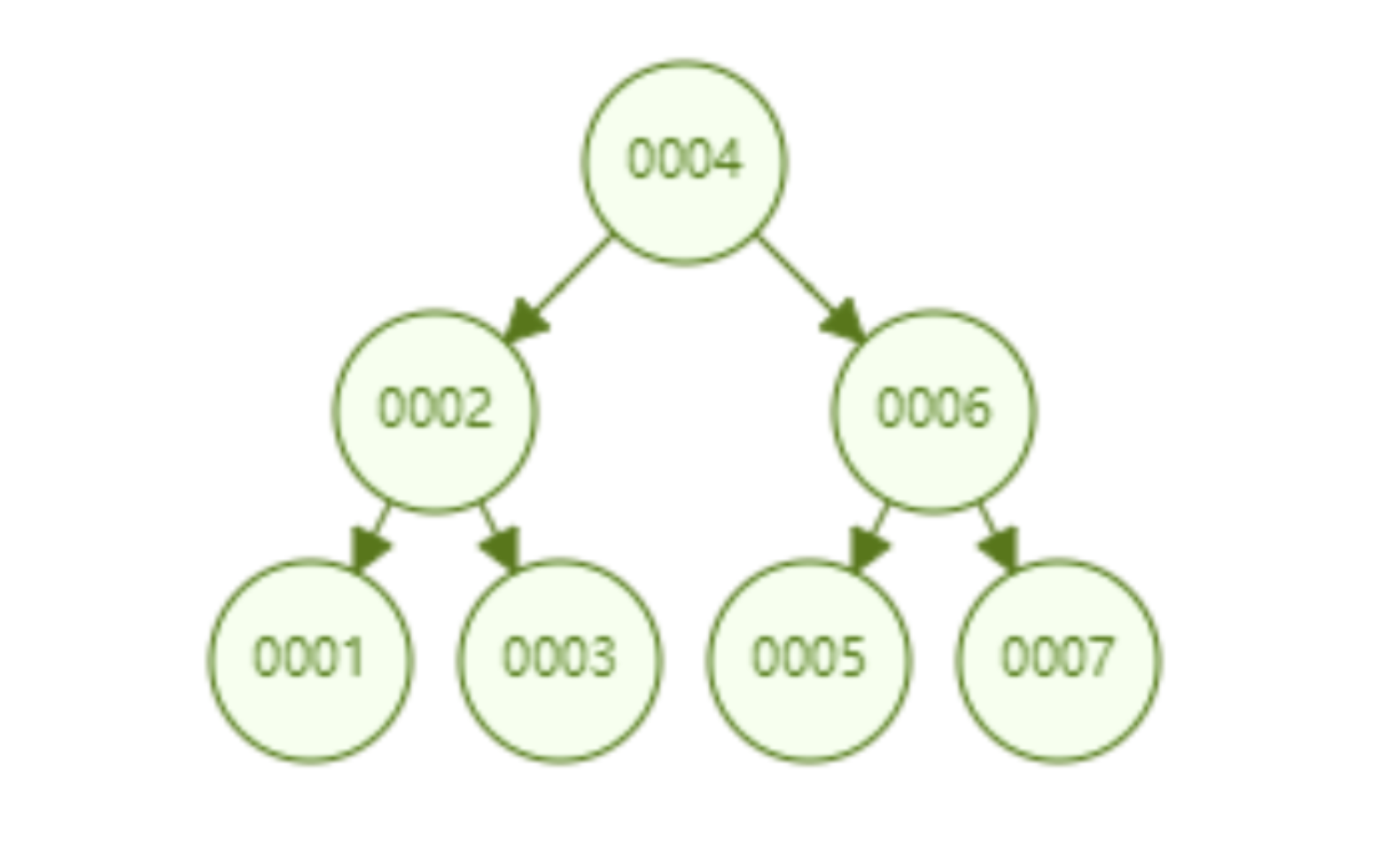
二叉查找树的时间复杂度是 O(lgn)，比如针对上面这个二叉树结构，我们需要计算比较 3 次就可以检索到 id=7 的数据，相对于直接遍历查询省了一半的时间，从检索效率上看来是能做到高速检索的。此外二叉树的结构能不能解决哈希索引不能提供的范围查找功能呢？

答案是可以的。观察上面的图，二叉树的叶子节点都是按序排列的，从左到右依次升序排列，如果我们需要找 id>5 的数据，那我们取出节点为 6 的节点以及其右子树就可以了，范围查找也算是比较容易实现。

但是普通的二叉查找树有个致命缺点：极端情况下会退化为线性链表，二分查找也会退化为遍历查找，时间复杂退化为 O（N），检索性能急剧下降。比如以下这个情况，二叉树已经极度不平衡了，已经退化为链表了，检索速度大大降低。此时检索 id=7 的数据的所需要计算的次数已经变为 7 了。

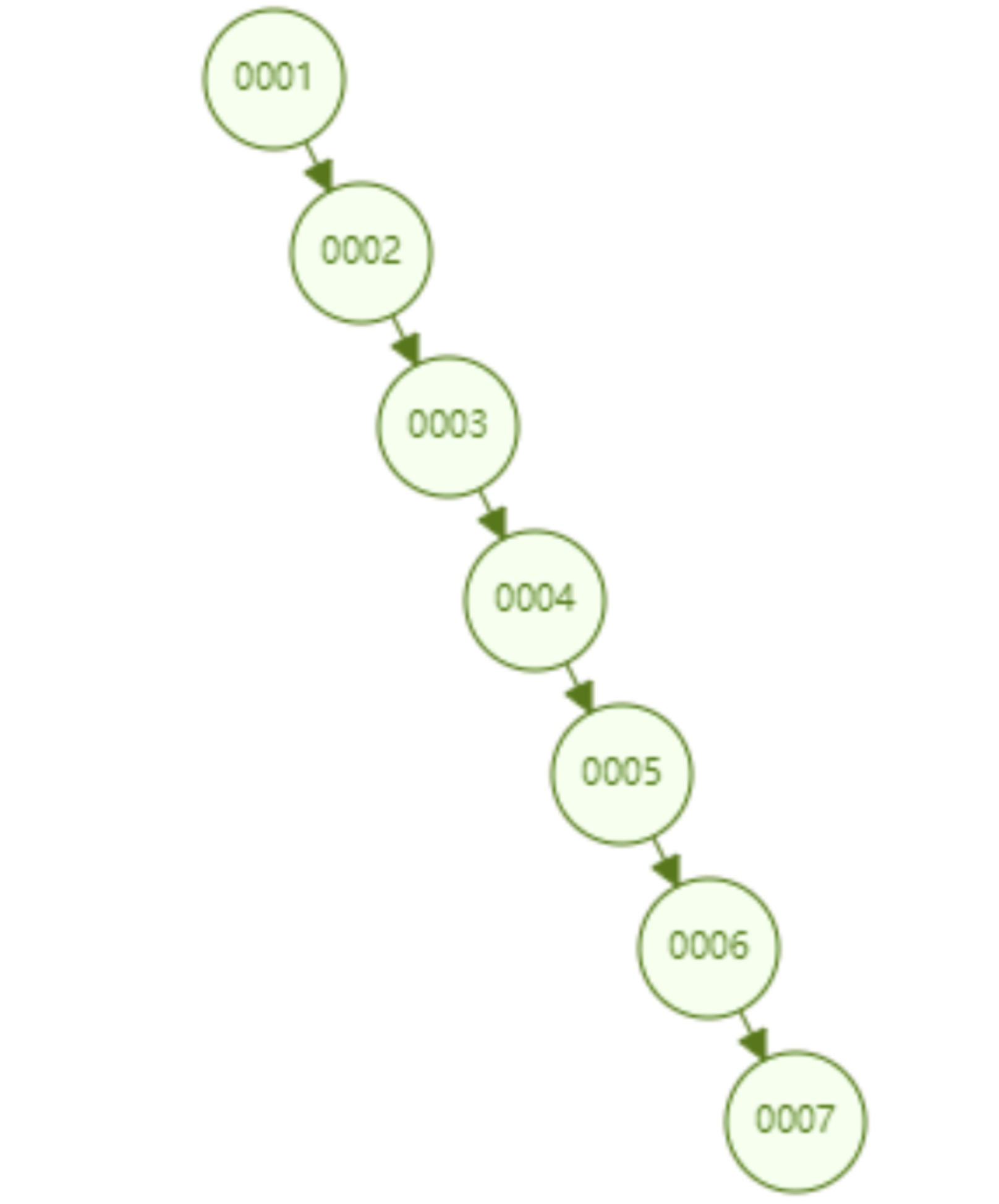
在数据库中，数据的自增是一个很常见的形式，比如一个表的主键是 id，而主键一般默认都是自增的，如果采取二叉树这种数据结构作为索引，那上面介绍到的不平衡状态导致的线性查找的问题必然出现。因此，简单的二叉查找树存在不平衡导致的检索性能降低的问题，是不能直接用于实现 Mysql 底层索引的。

AVL 树和红黑树

二叉查找树存在不平衡问题，因此学者提出通过树节点的自动旋转和调整，让二叉树始终保持基本平衡的状态，就能保持二叉查找树的最佳查找性能了。基于这种思路的自调整平衡状态的二叉树有 AVL 树和红黑树。

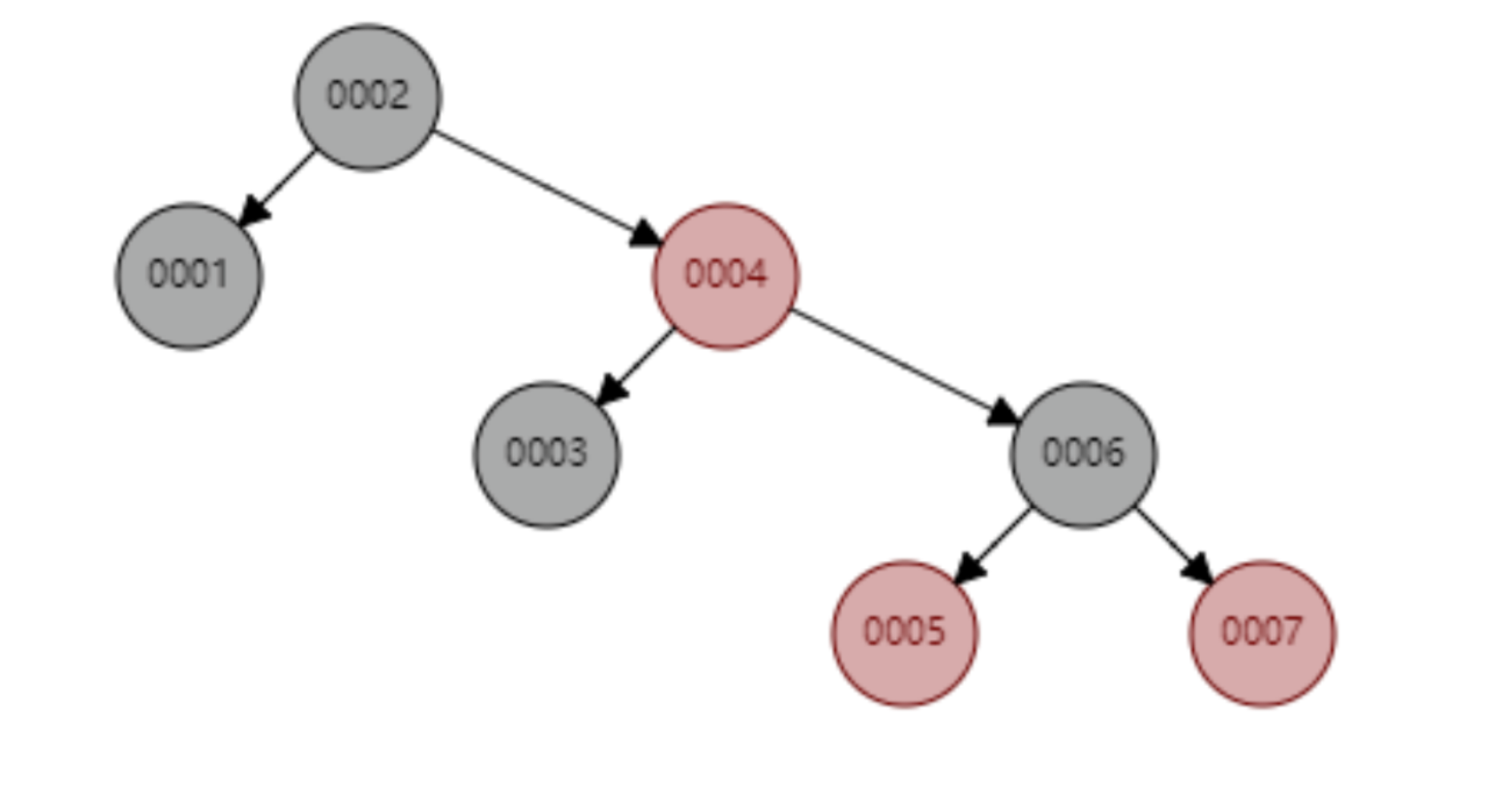
首先简单介绍红黑树，这是一颗会自动调整树形态的树结构，比如当二叉树处于一个不平衡状态时，红黑树就会自动左旋右旋节点以及节点变色，调整树的形态，使其保持基本的平衡状态（时间复杂度为 O（logn）），也就保证了查找效率不会明显减低。比如从 1 到 7 升序插入数据节点，如果是普通的二叉查找树则会退化成链表，但是红黑树则会不断调整树的形态，使其保持基本平衡状态，如下图所示。下面这个红黑树下查找 id=7 的所要比较的节点数为 4，依然保持二叉树不错的查找效率。

红黑树拥有不错的平均查找效率，也不存在极端的 O(n)情况，那红黑树作为 Mysql 底层索引实现是否可以呢？其实红黑树也存在一些问题，观察下面这个例子。
红黑树顺序插入 1~7 个节点，查找 id=7 时需要计算的节点数为 4。

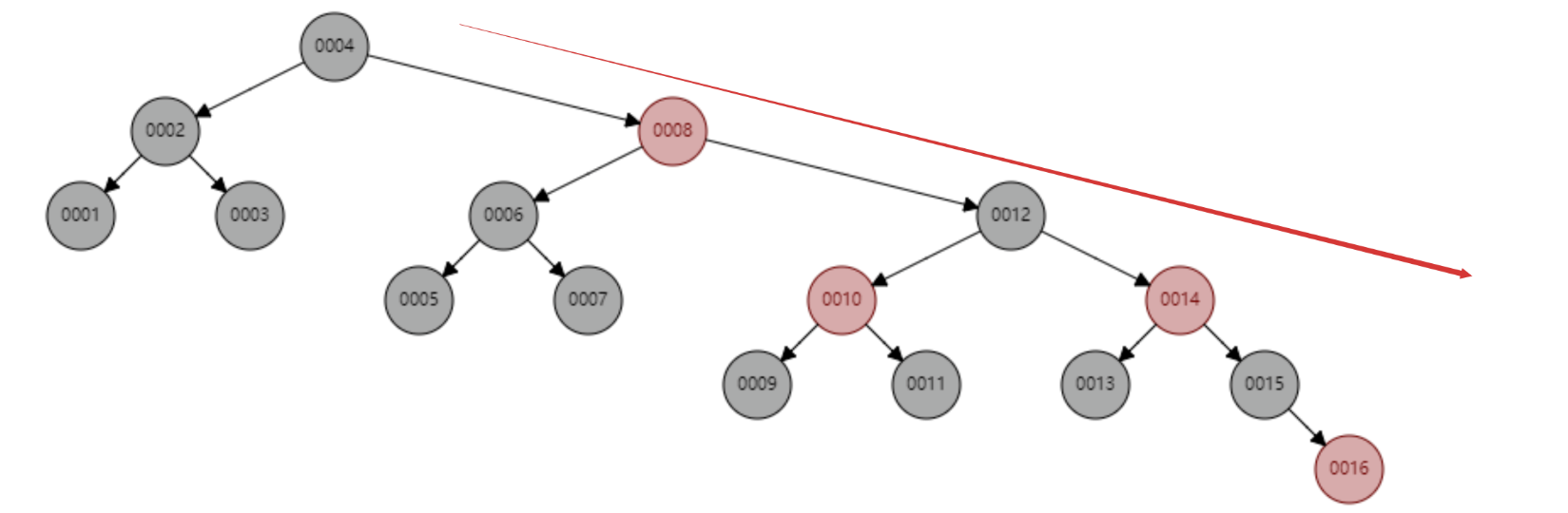
红黑树顺序插入 1~16 个节点，查找 id=16 需要比较的节点数为 6 次。观察一下这个树的形态，是不是当数据是顺序插入时，树的形态一直处于“右倾”的趋势呢？从根本上上看，红黑树并没有完全解决二叉查找树虽然这个“右倾”趋势远没有二叉查找树退化为线性链表那么夸张，但是数据库中的基本主键自增操作，主键一般都是数百万数千万的，如果红黑树存在这种问题，对于查找性能而言也是巨大的消耗，我们数据库不可能忍受这种无意义的等待的。

现在考虑另一种更为严格的自平衡二叉树 AVL 树。因为 AVL 树是个绝对平衡的二叉树，因此他在调整二叉树的形态上消耗的性能会更多。

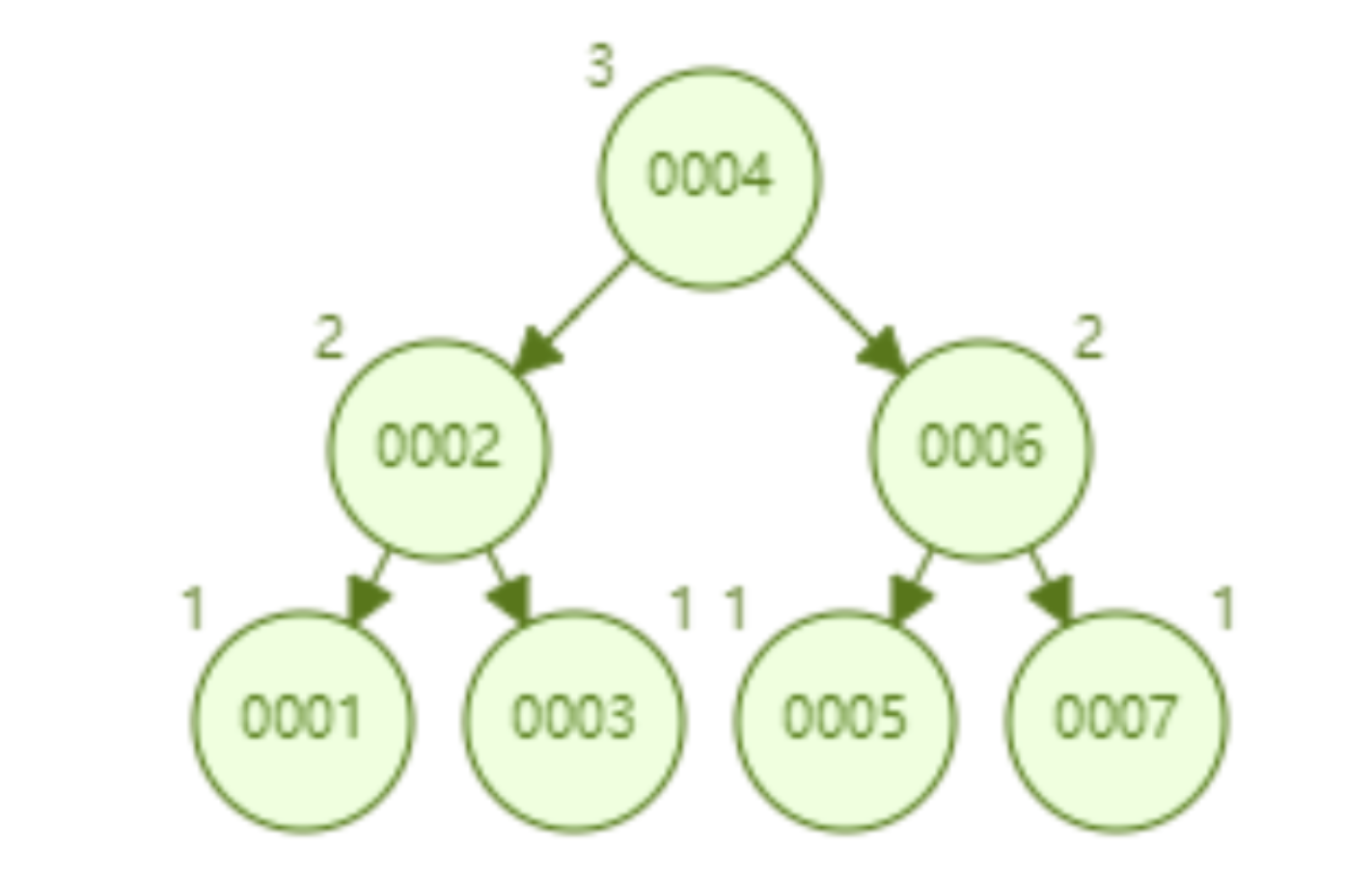
AVL 树顺序插入 1~7 个节点，查找 id=7 所要比较节点的次数为 3。

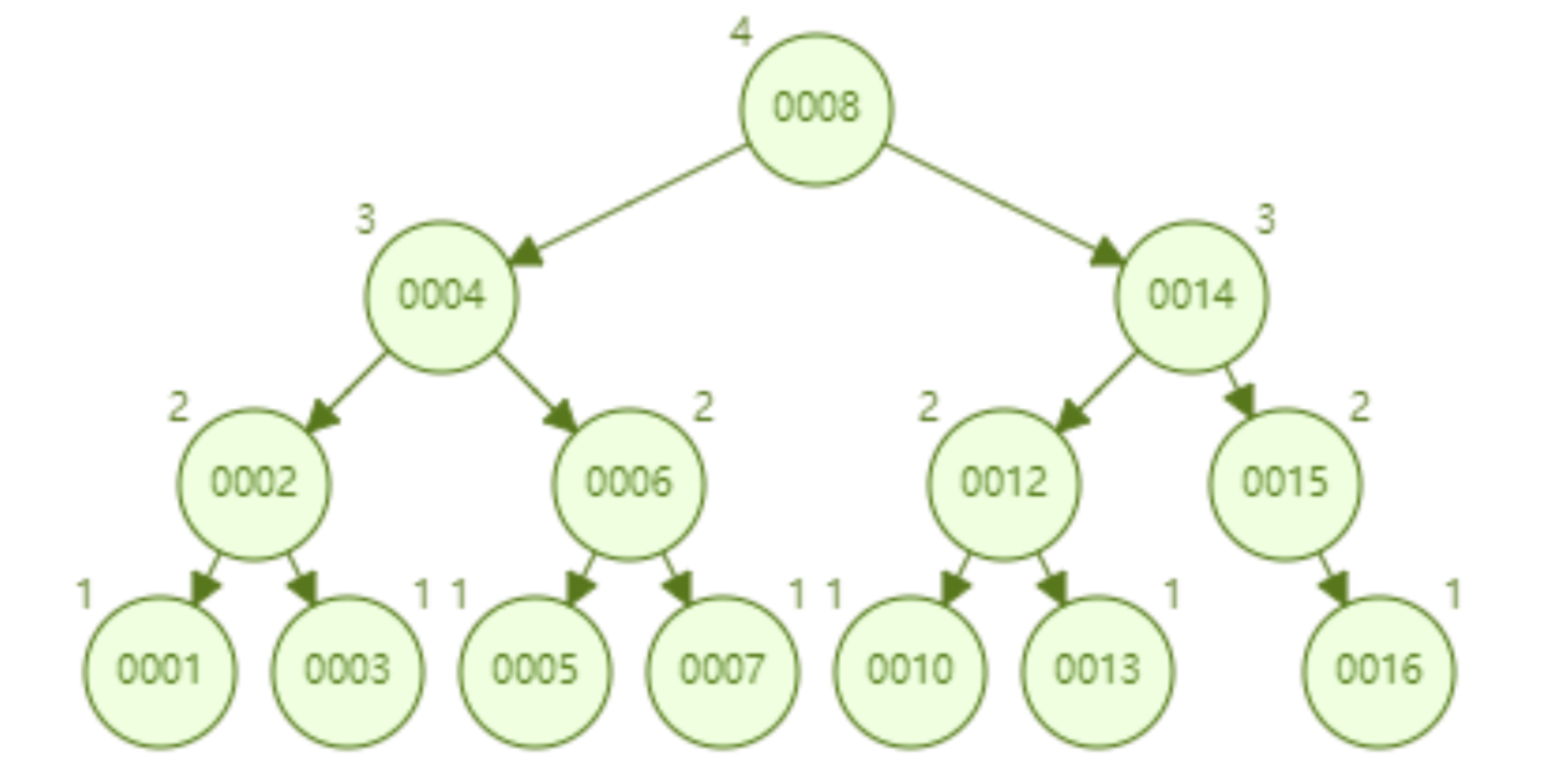
AVL 树顺序插入 1~16 个节点，查找 id=16 需要比较的节点数为 4。从查找效率而言，AVL 树查找的速度要高于红黑树的查找效率（AVL 树是 4 次比较，红黑树是 6 次比较）。从树的形态看来，AVL 树不存在红黑树的“右倾”问题。也就是说，大量的顺序插入不会导致查询性能的降低，这从根本上解决了红黑树的问题。

总结一下 AVL 树的优点：

1. 不错的查找性能（O（logn）），不存在极端的低效查找的情况。
   
2. 可以实现范围查找、数据排序。
   

看起来 AVL 树作为数据查找的数据结构确实很不错，但是 AVL 树并不适合做 Mysql 数据库的索引数据结构，因为考虑一下这个问题：

数据库查询数据的瓶颈在于磁盘 IO，如果使用的是 AVL 树，我们每一个树节点只存储了一个数据，我们一次磁盘 IO 只能取出来一个节点上的数据加载到内存里，那比如查询 id=7 这个数据我们就要进行磁盘 IO 三次，这是多么消耗时间的。所以我们设计数据库索引时需要首先考虑怎么尽可能减少磁盘 IO 的次数。

磁盘 IO 有个有个特点，就是从磁盘读取 1B 数据和 1KB 数据所消耗的时间是基本一样的，我们就可以根据这个思路，我们可以在一个树节点上尽可能多地存储数据，一次磁盘 IO 就多加载点数据到内存，这就是 B 树，B+树的的设计原理了。

B 树

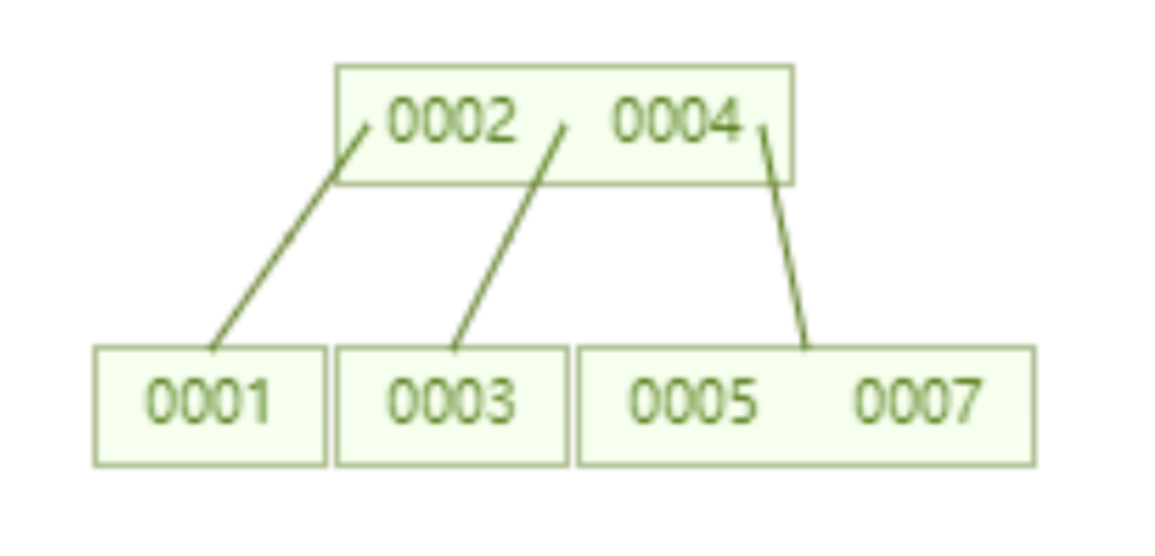
下面这个 B 树，每个节点限制最多存储两个 key，一个节点如果超过两个 key 就会自动分裂。比如下面这个存储了 7 个数据 B 树，只需要查询两个节点就可以知道 id=7 这数据的具体位置，也就是两次磁盘 IO 就可以查询到指定数据，优于 AVL 树。

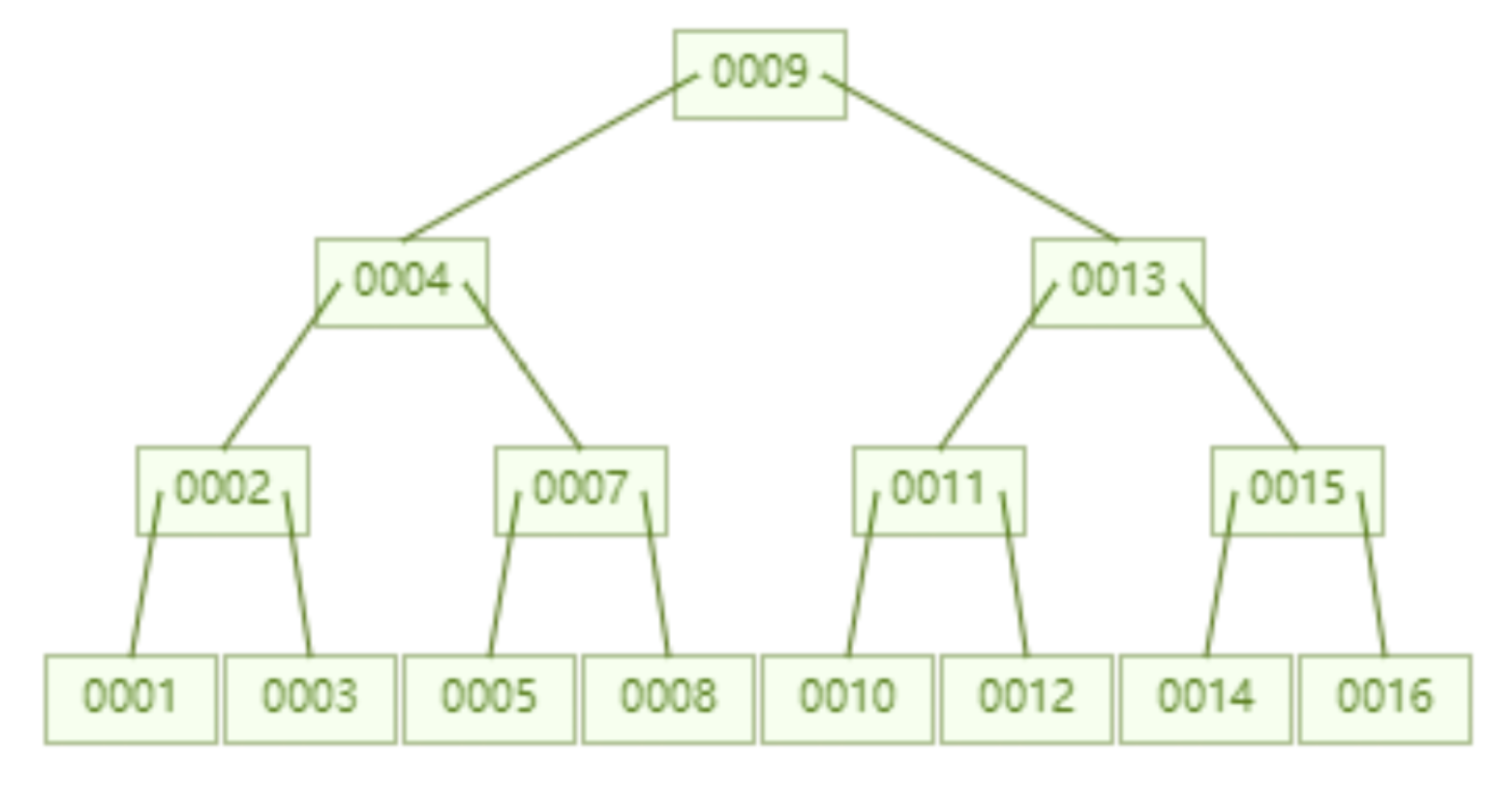
下面是一个存储了 16 个数据的 B 树，同样每个节点最多存储 2 个 key，查询 id=16 这个数据需要查询比较 4 个节点，也就是经过 4 次磁盘 IO。看起来查询性能与 AVL 树一样。

但是考虑到磁盘 IO 读一个数据和读 100 个数据消耗的时间基本一致，那我们的优化思路就可以改为：尽可能在一次磁盘 IO 中多读一点数据到内存。这个直接反映到树的结构就是，每个节点能存储的 key 可以适当增加。

当我们把单个节点限制的 key 个数设置为 6 之后，一个存储了 7 个数据的 B 树，查询 id=7 这个数据所要进行的磁盘 IO 为 2 次。

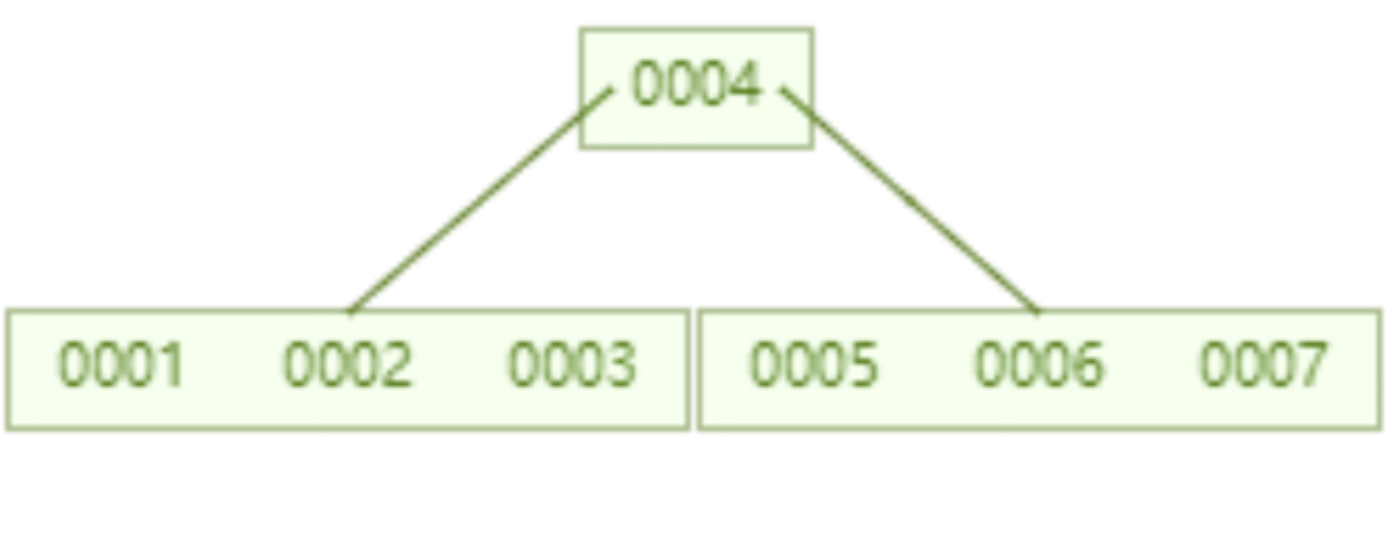
一个存储了 16 个数据的 B 树，查询 id=7 这个数据所要进行的磁盘 IO 为 2 次。相对于 AVL 树而言磁盘 IO 次数降低为一半。

所以数据库索引数据结构的选型而言，B 树是一个很不错的选择。总结来说，B 树用作数据库索引有以下优点：

1. 优秀检索速度，时间复杂度：B 树的查找性能等于 O（h*logn），其中 h 为树高，n 为每个节点关键词的个数；
   
2. 尽可能少的磁盘 IO，加快了检索速度；
   
3. 可以支持范围查找。
   
4. B+树
   

B 树和 B+树有什么不同呢？

第一，B 树一个节点里存的是数据，而 B+树存储的是索引（地址），所以 B 树里一个节点存不了很多个数据，但是 B+树一个节点能存很多索引，B+树叶子节点存所有的数据。

第二，B+树的叶子节点是数据阶段用了一个链表串联起来，便于范围查找。

通过 B 树和 B+树的对比我们看出，B+树节点存储的是索引，在单个节点存储容量有限的情况下，单节点也能存储大量索引，使得整个 B+树高度降低，减少了磁盘 IO。其次，B+树的叶子节点是真正数据存储的地方，叶子节点用了链表连接起来，这个链表本身就是有序的，在数据范围查找时，更具备效率。因此 Mysql 的索引用的就是 B+树，B+树在查找效率、范围查找中都有着非常不错的性能。

二、Innodb 引擎和 Myisam 引擎的实现

Mysql 底层数据引擎以插件形式设计，最常见的是 Innodb 引擎和 Myisam 引擎，用户可以根据个人需求选择不同的引擎作为 Mysql 数据表的底层引擎。我们刚分析了，B+树作为 Mysql 的索引的数据结构非常合适，但是数据和索引到底怎么组织起来也是需要一番设计，设计理念的不同也导致了 Innodb 和 Myisam 的出现，各自呈现独特的性能。

MyISAM 虽然数据查找性能极佳，但是不支持事务处理。Innodb 最大的特色就是支持了 ACID 兼容的事务功能，而且他支持行级锁。Mysql 建立表的时候就可以指定引擎，比如下面的例子，就是分别指定了 Myisam 和 Innodb 作为 user 表和 user2 表的数据引擎。

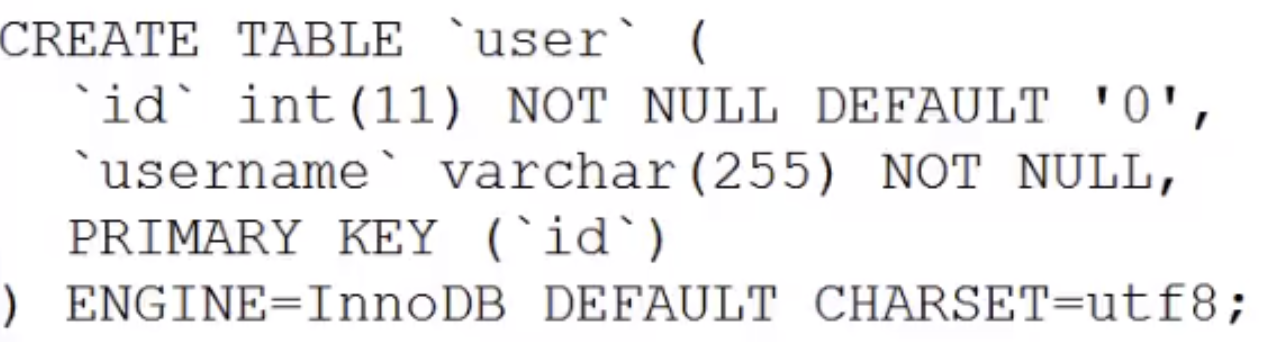
执行这两个指令后，系统出现了以下的文件，说明这两个引擎数据和索引的组织方式是不一样的。

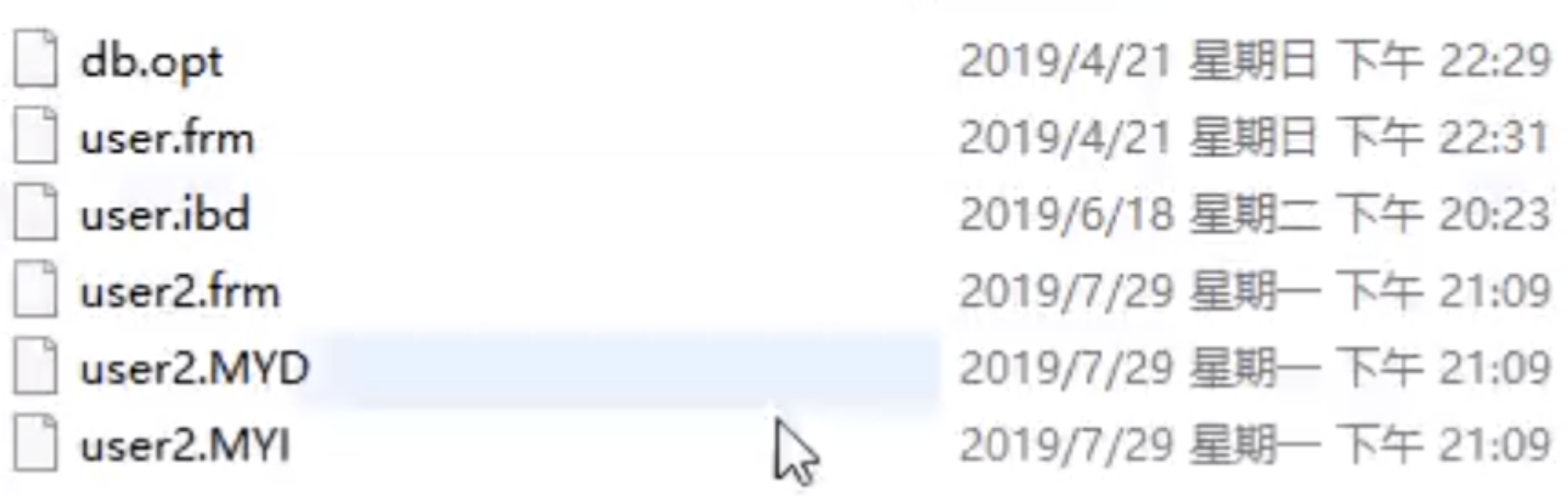
Innodb 创建表后生成的文件有：

• frm:创建表的语句
  
• idb:表里面的数据+索引文件
  

Myisam 创建表后生成的文件有

• frm:创建表的语句
  
• MYD:表里面的数据文件（myisam data）
  
• MYI:表里面的索引文件（myisam index）
  

从生成的文件看来，这两个引擎底层数据和索引的组织方式并不一样，MyISAM 引擎把数据和索引分开了，一人一个文件，这叫做非聚集索引方式；Innodb 引擎把数据和索引放在同一个文件里了，这叫做聚集索引方式。下面将从底层实现角度分析这两个引擎是怎么依靠 B+树这个数据结构来组织引擎实现的。

MyISAM 引擎的底层实现（非聚集索引方式）

MyISAM 用的是非聚集索引方式，即数据和索引落在不同的两个文件上。MyISAM 在建表时以主键作为 KEY 来建立主索引 B+树，树的叶子节点存的是对应数据的物理地址。我们拿到这个物理地址后，就可以到 MyISAM 数据文件中直接定位到具体的数据记录了。

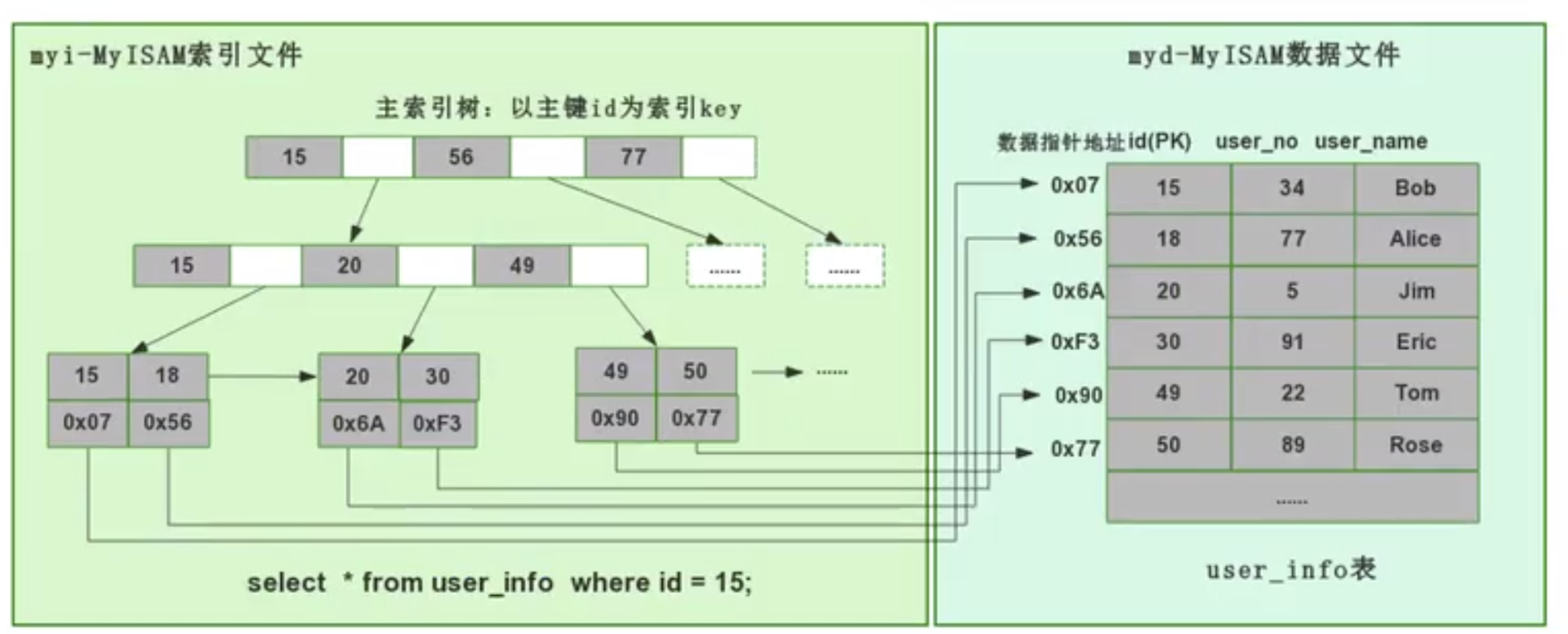
当我们为某个字段添加索引时，我们同样会生成对应字段的索引树，该字段的索引树的叶子节点同样是记录了对应数据的物理地址，然后也是拿着这个物理地址去数据文件里定位到具体的数据记录。

Innodb 引擎的底层实现（聚集索引方式）

InnoDB 是聚集索引方式，因此数据和索引都存储在同一个文件里。首先 InnoDB 会根据主键 ID 作为 KEY 建立索引 B+树，如左下图所示，而 B+树的叶子节点存储的是主键 ID 对应的数据，比如在执行 select * from user_info where id=15 这个语句时，InnoDB 就会查询这颗主键 ID 索引 B+树，找到对应的 user_name='Bob'。

这是建表的时候 InnoDB 就会自动建立好主键 ID 索引树，这也是为什么 Mysql 在建表时要求必须指定主键的原因。当我们为表里某个字段加索引时 InnoDB 会怎么建立索引树呢？比如我们要给 user_name 这个字段加索引，那么 InnoDB 就会建立 user_name 索引 B+树，节点里存的是 user_name 这个 KEY，叶子节点存储的数据的是主键 KEY。注意，叶子存储的是主键 KEY！拿到主键 KEY 后，InnoDB 才会去主键索引树里根据刚在 user_name 索引树找到的主键 KEY 查找到对应的数据。

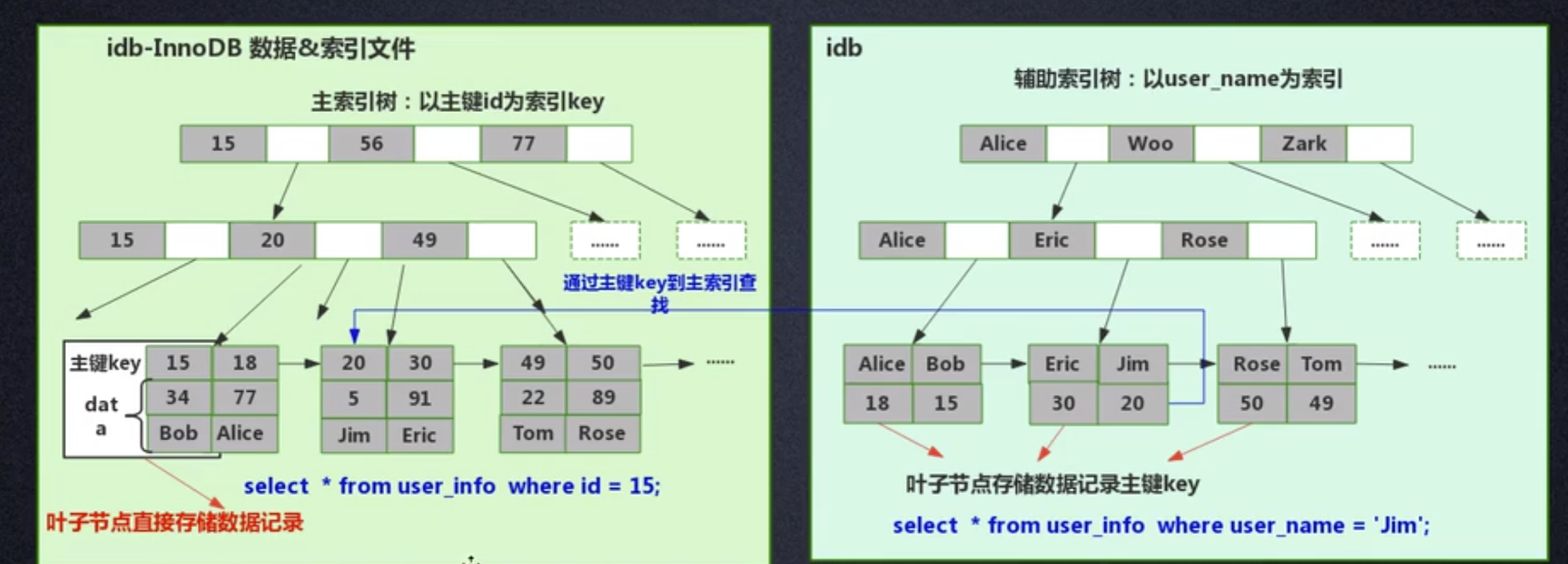
问题来了，为什么 InnoDB 只在主键索引树的叶子节点存储了具体数据，但是其他索引树却不存具体数据呢，而要多此一举先找到主键，再在主键索引树找到对应的数据呢?

其实很简单，因为 InnoDB 需要节省存储空间。一个表里可能有很多个索引，InnoDB 都会给每个加了索引的字段生成索引树，如果每个字段的索引树都存储了具体数据，那么这个表的索引数据文件就变得非常巨大（数据极度冗余了）。从节约磁盘空间的角度来说，真的没有必要每个字段索引树都存具体数据，通过这种看似“多此一举”的步骤，在牺牲较少查询的性能下节省了巨大的磁盘空间，这是非常有值得的。

在进行 InnoDB 和 MyISAM 特点对比时谈到，MyISAM 查询性能更好，从上面索引文件数据文件的设计来看也可以看出原因：MyISAM 直接找到物理地址后就可以直接定位到数据记录，但是 InnoDB 查询到叶子节点后，还需要再查询一次主键索引树，才可以定位到具体数据。等于 MyISAM 一步就查到了数据，但是 InnoDB 要两步，那当然 MyISAM 查询性能更高。

本文首先探讨了哪种数据结构更适合作为 Mysql 底层索引的实现，然后再介绍了 Mysql 两种经典数据引擎 MyISAM 和 InnoDB 的底层实现。最后再总结一下什么时候需要给你的表里的字段加索引吧：

1. 较频繁的作为查询条件的字段应该创建索引；
   
2. 唯一性太差的字段不适合单独创建索引，即使该字段频繁作为查询条件；
   
3. 更新非常频繁的字段不适合创建索引。
   

【相关推荐：mysql视频教程】

Das obige ist der detaillierte Inhalt vonmysql索引为什么快. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!