Eine kurze Analyse der Bildverzerrungskorrekturtechnologie zu den Schwierigkeiten der Front-End-Verarbeitung der Smart-Car-Wahrnehmung

Wir wissen, dass beim Aufnehmen von Bildern die ideale Position der Kamera senkrecht zur Aufnahmeebene ist, um sicherzustellen, dass das Bild entsprechend seinen ursprünglichen geometrischen Proportionen wiedergegeben werden kann. Bei der tatsächlichen Anwendung intelligenter Autos erfordert die Karosseriesteuerung jedoch aufgrund der Einschränkungen der Karosseriestruktur einen bestimmten Vorschauabstand. Die horizontalen und vertikalen Scanflächen der Kamera dehnen sich normalerweise fächerförmig aus. und die Kamera hat im Allgemeinen Kontakt mit dem Boden. Installieren Sie sie in einem Winkel. Das Vorhandensein dieses Winkels führt zu gewissen Bildverzerrungen am Bildrand. Das Ergebnis der Verzerrung ist eine Reihe ähnlicher Probleme wie folgt bei der Nachbearbeitung von Bildern:

1) Vertikale Linien werden als diagonale Linien fotografiert, was zu Fehlern bei der Neigungsberechnung führt

2) Verzerrungen können zu weit entfernten Biegungen führen Die Komprimierung führt zu Fehlern bei der Krümmungsberechnung usw.; Bei den oben genannten Arten kann es zu Problemen bei der gesamten Bildwahrnehmung kommen, wenn die Verzerrung nicht richtig behandelt wird, was zu größeren Risiken für die Gesamtbildqualität und die anschließende Erkennung des neuronalen Netzwerks führt. Um den Echtzeitsteuerungsanforderungen intelligenter Autos gerecht zu werden, ist es im Allgemeinen erforderlich, entsprechende Korrekturalgorithmen für Kamerabildverzerrungen in praktischen Anwendungsszenarien vorzuschlagen.

01 Die wichtigsten Arten von Verzerrungen in Smart-Autos

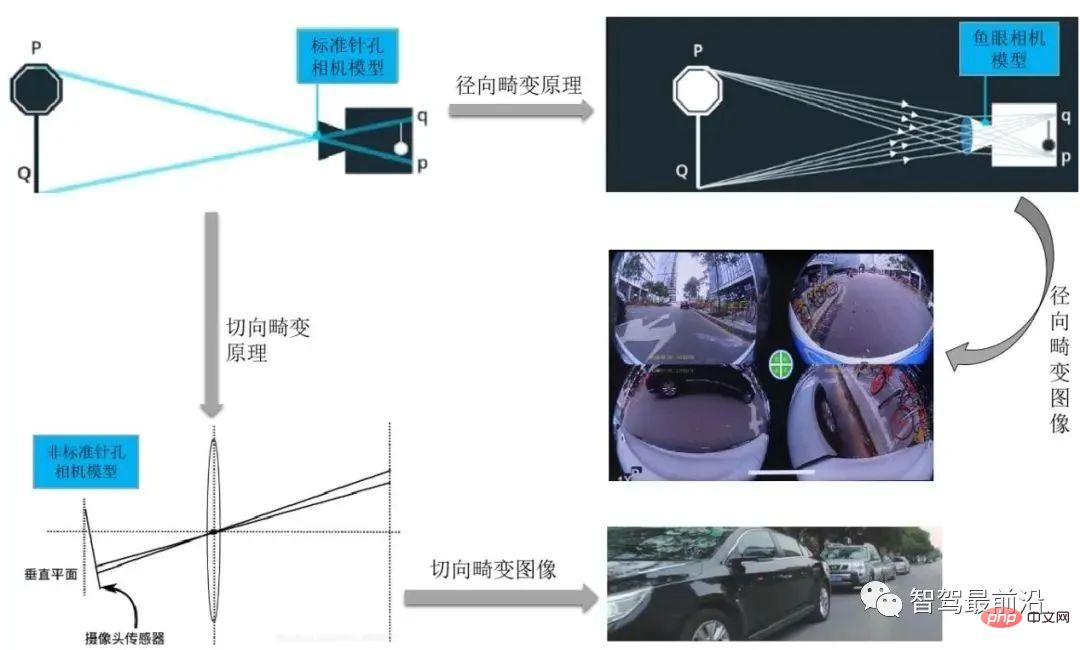
Zu den Kameraverzerrungen gehören Radialverzerrung, Tangentialverzerrung, Zentrifugalverzerrung, Verzerrung durch dünne Prismen usw. Zu den Hauptkameraverzerrungen bei Smart-Autos gehören Radialverzerrung und Tangentialverzerrung .

Radiale Verzerrung wird in Tonnenverzerrung und Kissenverzerrung unterteilt.

Normalerweise verwendet die in unserem intelligenten Parksystem verwendete Rundumsichtkamera Weitwinkelaufnahmen und der entsprechende Verzerrungstyp ist normalerweise eine radiale Verzerrung. Die Hauptursache für die radiale Verzerrung ist die unregelmäßige Änderung der radialen Krümmung der Linse, die zu einer Verzerrung des Bildes führt. Das Merkmal dieser Verzerrung ist, dass der Hauptpunkt das Zentrum ist und sich entlang der radialen Richtung bewegt Je weiter es entfernt ist, desto größer ist die erzeugte Verformung. Eine starke radiale Verzerrung eines Rechtecks ​​muss in ein ideales lineares Linsenbild korrigiert werden, bevor es in den Back-End-Verarbeitungsprozess eintreten kann.

Die im Allgemeinen in Fahrsystemen verwendeten Front-, Seiten- und Rückfahrkameras verwenden allgemeine CMOS-Prozesskameras für die Aufnahme, und da der Installationsprozess der Front-Seitenkamera möglicherweise nicht gewährleistet, dass das Objektiv und Die Abbildungsfläche ist streng parallel, und gleichzeitig kann es an einem Herstellungsfehler liegen, dass das Objektiv nicht parallel zur Abbildungsebene ist, was zu einer tangentialen Verzerrung führt. Dieses Phänomen tritt normalerweise auf, wenn der Bildgeber an der Kamera angebracht ist.

In den Modellen für radiale Verzerrung und tangentiale Verzerrung sind sie in einer 5*1-Matrix angeordnet, einschließlich k1, k2, p1, p2, k3. wird oft in Form einer Mat-Matrix definiert.

Für die Verzerrungskorrektur sind diese 5 Parameter die 5 Verzerrungskoeffizienten der Kamera, die bei der Kamerakalibrierung ermittelt werden müssen. Die Parameter k1, k2 und k3 werden als radiale Verzerrungsparameter bezeichnet, wobei k3 ein optionaler Parameter ist. Bei Kameras mit starker Verzerrung (z. B. Augenkameras) können auch k4, k5 und k6 vorhanden sein. Die tangentiale Verzerrung kann durch zwei Parameter p1 und p2 dargestellt werden: Bisher wurden insgesamt fünf Parameter ermittelt: K1, K2, K3, P1, P2. Diese fünf Parameter sind zur Beseitigung der Verzerrung notwendig und werden auch Verzerrungsvektoren genannt werden als externe Parameter der Kamera bezeichnet.

Daher kann nach Erhalt dieser 5 Parameter die durch die Linsenverzerrung verursachte Verformungsverzerrung des Bildes korrigiert werden. Die folgende Abbildung zeigt den Effekt nach der Korrektur entsprechend dem Linsenverzerrungskoeffizienten:

Finden Sie dies durch 5 Verzerrung Koeffizienten Die korrekte Positionsformel des Punktes auf der Pixelebene lautet wie folgt:

Der verzerrte Punkt kann über die interne Parametermatrix auf die Pixelebene projiziert werden, um die korrekte Position (u, v) des zu erhalten Punkt auf dem Bild:

02 Bildverzerrungskorrekturmethode

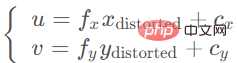
Unterscheidet sich von der Methode des Kameramodells, Bildentzerrung Um Objektivdefekte zu kompensieren, wird das Originalbild radial/tangential entzerrt und anschließend das Kameramodell verwendet. Der Umgang mit Bildverzerrungen hängt hauptsächlich davon ab, welches Kameramodell für die Bildprojektion ausgewählt werden soll.

Typische Kameramodell-Projektionsmethoden umfassen das sphärische Modell und das zylindrische Modell. #? # Normalerweise erzeugen Fischaugenobjektive eine starke Verformung. Während des Bildgebungsprozesses einer gewöhnlichen Kamera ist eine gerade Linie immer noch eine gerade Linie einer bestimmten Größe, wenn sie auf die Bildebene projiziert wird, aber wenn das Bild aufgenommen wird Wenn eine Fischaugenkamera auf die Bildebene projiziert wird, wird dies zu einer sehr großen und langen geraden Linie, und in einigen Szenen wird sogar die Erkennung gerader Linien auf unendlich projiziert, sodass das Lochkameramodell das Fischaugenobjektiv nicht modellieren kann.

Um eine möglichst große Szene in eine begrenzte Bildebene zu projizieren, setzt sich die erste Version des Fischaugenobjektivs aus mehr als einem Dutzend verschiedener Linsen zusammen Dabei wird das einfallende Licht unterschiedlich stark gebrochen und auf eine Bildebene begrenzter Größe projiziert, wodurch das Fischaugenobjektiv im Vergleich zu herkömmlichen Objektiven ein größeres Sichtfeld hat. Untersuchungen zeigen, dass das Modell, dem Fischaugenkameras bei der Bildgebung folgen, ungefähr einem Einheitskugelprojektionsmodell entspricht. Um sich besser an den Ableitungsprozess des Kamera-Lochlochmodells anzupassen, besteht die übliche Methode darin, den Prozess der Projektion auf das sphärische Kameramodell zu verwenden.

Die Analyse des Fischaugenkamera-Bildgebungsprozesses kann in zwei Schritte unterteilt werden:

#🎜🎜 #Dreidimensional Der Raumpunkt wird linear auf eine Kugel projiziert. Natürlich handelt es sich bei dieser Kugel um die virtuelle Kugel, von der wir annehmen, dass ihr Mittelpunkt mit dem Ursprung der Kamerakoordinaten zusammenfällt.

Der Punkt auf der Einheitskugel wird auf die Bildebene projiziert. Dieser Vorgang ist nichtlinear.

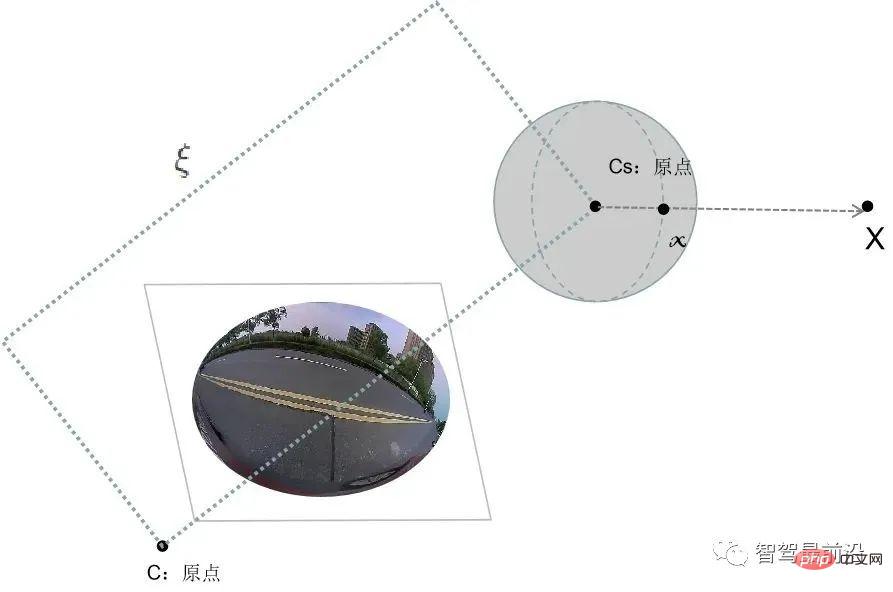
Die folgende Abbildung zeigt den Bildverarbeitungsprozess von einer Fischaugenkamera zu einer sphärischen Kamera in einem intelligenten Fahrsystem. Nehmen Sie an, dass der Punkt im Kamerakoordinatensystem X=(x,y,z) und die Pixelkoordinate x=(u,v) ist. Dann wird sein Projektionsprozess wie folgt ausgedrückt:​​ Sammeln Sie mit einer Kamera dreidimensionale Punkte im Weltkoordinatensystem und projizieren Sie die Bildpunkte im Bildkoordinatensystem auf die normalisierten sphärischen Einheitskoordinaten #

• 2) Versetzen Sie das Kamerakoordinatenzentrum um Einheiten entlang der Z-Achse und erhalten Sie Folgendes: # 🎜🎜#

# 🎜🎜#

3) Betrachten Sie die Einheitskugel und normalisieren Sie die Kugel auf 1 Einheit: # 🎜🎜#

#🎜 🎜#

4) Transformieren Sie das sphärische Projektionsmodell in das Lochmodell, um das entsprechende zu erhalten Hauptpunktkoordinaten, die zum Herstellen einer Korrespondenz verwendet werden können. Das Standardmodell des Kamerakoordinatensystems:

#🎜 🎜#2. Zylinderkoordinatenprojektion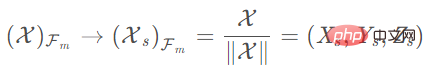

Bei Endgeräten wie Front- und Seitenansichtkameras erzeugen die aufgenommenen Bilder in der Regel hauptsächlich tangentiale Verzerrungen. Bei tangentialer Verzerrung empfiehlt sich in der Regel die Verwendung eines zylindrischen Kameramodells. Der Vorteil besteht darin, dass der Benutzer in einer Panoramaansicht wie einer Fischaugenkamera die Sichtlinie beliebig wechseln und auch die Perspektive ändern kann auf einer Sichtlinie, um den Effekt einer Annäherung oder Entfernung zu erzielen. Gleichzeitig sind zylindrische Panoramabilder auch einfacher zu verarbeiten, da die zylindrische Oberfläche entlang der Achse geschnitten und auf einer Ebene entfaltet werden kann Zylindrische Panoramabilder können oft nicht sehr genau kalibriert werden. Nutzer haben einen 360-Grad-Blickwinkel in horizontaler Richtung und können auch bestimmte Blickwinkeländerungen in vertikaler Richtung vornehmen, allerdings ist der Winkelbereich begrenzt, da die Bildqualität des zylindrischen Modells gleichmäßiger und die Details realistischer sind Es hat ein breiteres Anwendungsspektrum.

Im Allgemeinen lassen sich die wesentlichen Vorteile des zylindrischen Panoramas in den folgenden zwei Punkten zusammenfassen:

1) Die Aufnahmemethode für ein einzelnes Foto ist einfacher als die Aufnahmemethode für Würfelform und Kugelform. Gewöhnliche Fahrzeugkameras (z. B. Front- und Seitenkameras) können grundsätzlich Originalbilder erhalten.

2) Das zylindrische Panorama lässt sich leicht zu einem rechteckigen Bild erweitern, das direkt in gängigen Computerbildformaten gespeichert und abgerufen werden kann. Das zylindrische Panorama ermöglicht, dass der Rotationswinkel der Blickrichtung des Teilnehmers in vertikaler Richtung weniger als 180 Grad beträgt. In den meisten Anwendungen reicht jedoch eine 360-Grad-Panoramaszene in horizontaler Richtung aus, um räumliche Informationen auszudrücken.

Hier konzentrieren wir uns auf den Algorithmus zur Verwendung einer zylindrischen Kamera zur Korrektur der Verzerrung des Originalbilds. Tatsächlich handelt es sich hierbei um einen Prozess, bei dem die Zuordnungsbeziehung von der virtuellen Kamera zur Originalkamera ermittelt wird . Die virtuelle Kamera bezieht sich hier auf die Abbildungsbeziehung zwischen realen Bildern und generierten zylindrischen Bildern.

Die folgende Abbildung zeigt den Bildverarbeitungsprozess beim Konvertieren von gewöhnlichen Autokameraaufnahmen zu zylindrischen Kameras in einem intelligenten Fahrsystem. Unter anderem besteht das Wesentliche beim Erhalten des virtuellen Kamerabilds darin, die Zuordnungsbeziehung zwischen der virtuellen Kamera und der Originalkamera zu ermitteln. Der allgemeine Prozess ist wie folgt:

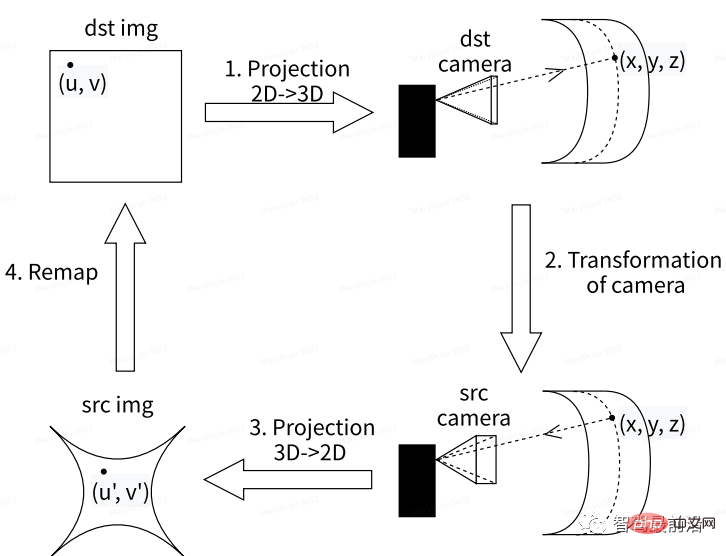
Zuerst das Originalvideo von vorne/von der Seite Das Bild kann als Zielbild festgelegt werden. dst img; wobei der Hauptpunkt (u, v) auf der Zielkarte der Basispunkt für die Rückprojektionstransformation von 2D in 3D ist, um die Zielkamera-Koordinatenkarte zu rekonstruieren Die Position des Punktes im Weltkoordinatensystem (x, y, z); dann kann das entsprechende ursprüngliche Kamerabild Src unter der virtuellen Kamera durch den Projektionstransformationsalgorithmus in das dreidimensionale Koordinatensystem erhalten werden; Erhalten Sie das Bild Src img (u', v'), indem Sie eine 3D- in eine 2D-Projektion des Originalkamerabilds umwandeln. Dieses Bild kann rekonstruiert werden, um das Originalbild dst img unter der virtuellen Kamera wiederherzustellen.

Aus dem zylindrischen Kameramodell ist ersichtlich, dass die Transformationsformel vom zylindrischen Kameramodell zum Lochkameramodell wie folgt lautet:

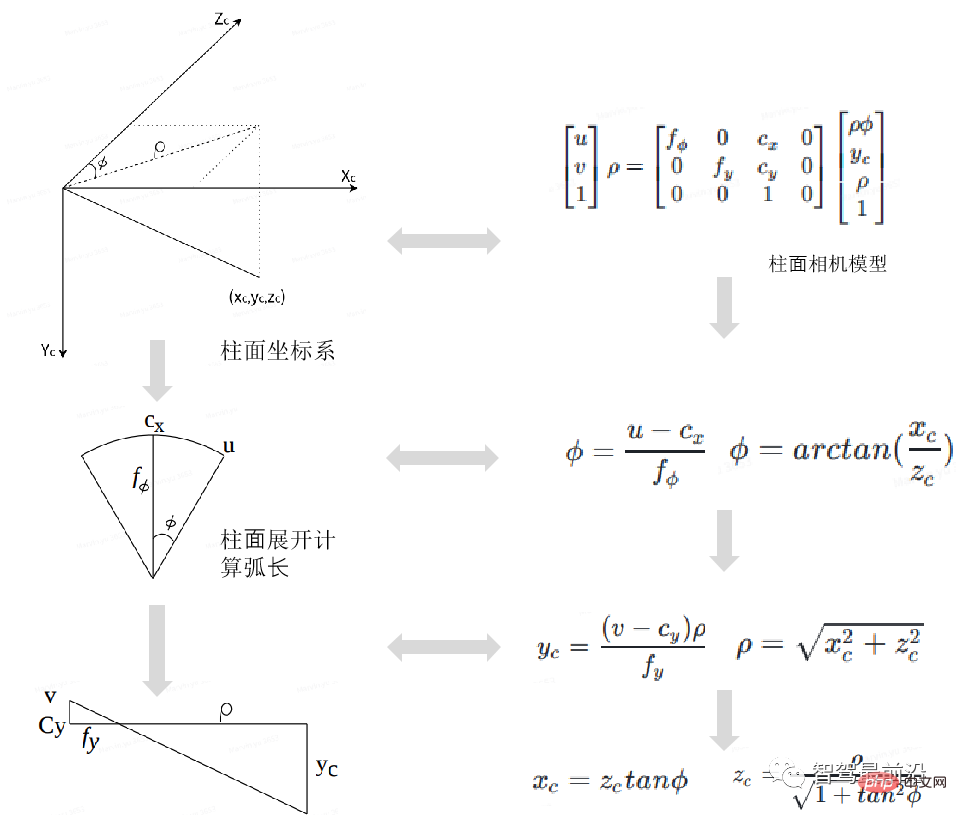
In der obigen Formel stellen u und v dar Hauptpunkte der Lochkameraebene (im Pixelkoordinatensystem auch Koordinaten genannt), fx, fy, cx, cy stellen die beiden Koordinatenachsen-Ablenkungsparameter dar, die durch Herstellungs- oder Installationsfehler verursacht werden. Der Hauptpunkt wird mit dem Radiusabstand im Zylinderkoordinatensystem multipliziert, um die entsprechende Projektion auf die Zylinderkoordinaten zu erhalten.

ρ wird verwendet, um eine polynomische Annäherung an den 2D->3D-Raum durchzuführen. Wenn Tdst = Tsrc ist, nimmt ρ unterschiedliche Werte an, und zwar aus dem 3D-Raum->Seiten-/Vorderansichtsraum der in 2D erhaltenen virtuellen Kamera ist derselbe, wenn Tdst! =Tsrc, das erhaltene virtuelle Kamerabild ändert sich mit ρ. Für eine gegebene zylindrische 2D-Position (u, v) können unter einer gegebenen ρ-Bedingung die 3D-Kamerakoordinaten xc, yc, zc im dst-Kamera-Zylinderkoordinatensystem gemäß der obigen Formel berechnet werden.

Φ wird verwendet, um eine polynomische Näherung durchzuführen. Φ ist der Winkel zwischen dem einfallenden Licht und der Bildebene. Dieser Wert ist den Parametern einer Fischaugenkamera sehr ähnlich.

Der nächste Schritt ist der Kameratransformationsprozess, der wie folgt zusammengefasst werden kann.

Stellen Sie zunächst die Bildauflösung der virtuellen Kamera auf die Auflösung der IPM-Karte aus der Vogelperspektive ein, die Sie erhalten möchten. Der Hauptpunkt des virtuellen Kamerabilds ist die Mitte der IPM-Kartenauflösung (im Allgemeinen unter der Annahme, dass kein Offset eingestellt ist). ). Zweitens stellen Sie fx, fy und die Kameraposition der virtuellen Kamera ein. Die Höhe ist auf 1 eingestellt, was der Einstellungsmethode von fx und fy entspricht. Der Offset von y kann je nach Bedarf geändert werden. Daraus können die Kamerakoordinaten der dst-Kamera (xc, yc, zc) dst gemäß den externen Parametern (R, T) dst der Zielkamera dst in die Koordinaten des Beobachtungskoordinatensystems vcs konvertiert und dann mit den externen Parametern kombiniert werden Parameter der src-Kamera (R, T) src, konvertieren Sie VCS-Koordinaten in src-Kamera-Kamerakoordinaten (xc, yc, zc) src.

03 Zusammenfassung

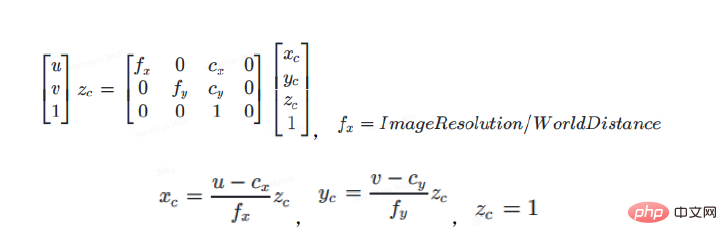
Da Fahrzeugkameras in der Regel mit unterschiedlichen Abbildungsobjektiven ausgestattet sind, macht es dieser Mehrelementaufbau unmöglich, einfach das ursprüngliche Lochkameramodell zur Analyse der Brechungsbeziehung zu verwenden von fahrzeugmontierten Kameras. Insbesondere bei Fischaugenkameras ist die durch diesen Brechungsindex verursachte Bildverzerrung aufgrund der Notwendigkeit, den Sichtbereich zu erweitern, noch deutlicher. In diesem Artikel konzentrieren wir uns auf die Entzerrungsmethode, die an verschiedene Arten von visuellen Sensoren in intelligenten Fahrsystemen angepasst ist. Dabei projizieren wir das Bild im Weltkoordinatensystem hauptsächlich in das virtuelle sphärische Koordinatensystem und das virtuelle zylindrische Koordinatensystem Verlassen Sie sich auf die 2D->3D-Kameratransformation, um Verzerrungen zu beseitigen. Einige Algorithmen wurden aufgrund langjähriger Praxis im Vergleich zum klassischen Entverzerrungsalgorithmus verbessert.

Das obige ist der detaillierte Inhalt vonEine kurze Analyse der Bildverzerrungskorrekturtechnologie zu den Schwierigkeiten der Front-End-Verarbeitung der Smart-Car-Wahrnehmung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!