PHP-Datenstruktur-Graph-Durchquerung: Tiefe zuerst und Breite zuerst

Graph Traversal: Tiefe zuerst und Breite zuerst

Im vorherigen Artikel „PHP-Datenstruktur – Graphspeicherstruktur“ haben wir die relevanten Speicherstrukturen von Graphen kennengelernt, nämlich Adjazenzmatrix und Adjazenzliste. Sie stellen die beiden typischsten Arten der sequentiellen Speicherung bzw. der verketteten Speicherung dar. Nachdem wir nun die Datenstrukturen haben, besteht unser nächster Schritt natürlich darin, zu lernen, wie man diese Datenstrukturen bedient, was den Algorithmusteil darstellt. Unabhängig davon, ob es sich um einen Graphen oder einen Baum handelt, ist das Durchlaufen ein sehr wichtiger Teil. Heute lernen wir zunächst die beiden grundlegendsten Methoden zum Durchlaufen von Diagrammen.

Die Baumdurchquerung entwickelte sich zur Graphendurchquerung

Erinnern Sie sich noch daran, dass wir bei der Untersuchung von Bäumen über die Vorbestellungs-, In-Reihenfolge-, Nachbestellungs- und Ebenenreihenfolge-Durchquerungsformen gesprochen haben? Tatsächlich können Vorbestellung, Mittelbestellung und Nachbestellung als eine Art Durchquerungsmethode betrachtet werden. Sie alle verwenden die Stapelstruktur zum Durchlaufen. Das Merkmal besteht darin, zuerst zum schwarzen Pfad zu gehen und dann zum nicht durchquerten Pfad zurückzukehren Weg. Beim Layer-Order-Traversal wird eine Warteschlange verwendet, um Layer für Layer zu durchlaufen. Sein Merkmal besteht darin, zuerst die untergeordneten Knoten und dann nacheinander die Knoten der nächsten Ebene jedes untergeordneten Knotens zu durchlaufen.

Nachdem Sie die Baumdurchquerungsmethode überprüft haben, wird es sehr einfach sein, die Diagrammdurchquerungsmethode zu erlernen, da bei der Diagrammdurchquerung die grundlegendsten beiden Durchquerungsformen auf Stapel und Warteschlange basieren. Ihre Namen unterscheiden sich lediglich geringfügig. Die stapelbasierte Durchquerungsmethode wird als Tiefendurchquerung bezeichnet, während die warteschlangenbasierte Durchquerungsmethode als Breitendurchquerung bezeichnet wird. Tatsächlich entspricht es dem Durchlauf erster, mittlerer und letzter Ordnung und dem Durchlauf der Schichtordnung im Baum. Im Wesentlichen gibt es keinen großen Unterschied.

[Empfohlen:PHP-Video-Tutorial]

Tiefendurchquerung

Wir beginnen immer noch mit der Stapeldurchquerungsmethode, bei der es sich im Bild um die Form der Tiefendurchquerung handelt. Für den Stapel werden kontinuierlich neue Knoten auf den Stapel verschoben, bis festgestellt wird, dass er keine anderen untergeordneten Knoten hat. Anschließend wird der ursprüngliche Pfad zurückgegeben. Wenn festgestellt wird, dass ein Knoten andere Knoten hat, wird der untergeordnete Knoten auf den Stapel verschoben Dies ist die Idee des Deep Traversal.

Hier ist zu beachten, dass wir die besuchten Knoten aufzeichnen müssen. Wenn mehrere Knoten mit Pfaden mit einem bestimmten Knoten verbunden sind, stellen Sie sicher, dass dieser Knoten nur einmal besucht wurde. Dies ist der größte Unterschied zur Baumstruktur, da der Baum ganz nach unten verläuft, es keine Verbindung zwischen horizontalen Knoten gibt und ein Knoten nur einen übergeordneten Knoten hat. In einem Diagramm kann jeder Knoten mit jedem anderen Knoten verknüpft sein.

Adjazenzmatrix

Schauen wir uns zunächst die Implementierung des Tiefendurchlaufalgorithmus für die Adjazenzmatrix an. Es macht nichts, wenn Sie es jetzt nicht verstehen. Scrollen Sie nach unten, um die Abbildungen zu sehen, und lesen Sie sie dann gemeinsam. Eine bessere Lösung ist natürlich, es selbst auszuführen.

$visited = []; // 已访问结点 function DFS_AM($graphArr, $x) { global $visited; echo "节点：{$x}", PHP_EOL; $visited[$x] = true; // 当前结点标记为已访问 // y 就是邻接矩阵中的横行 for ($y = 1; $y <= count($graphArr); $y++) { // 循环判断第 [x][y] 个数据是否为 1，也就是是否有边 // 并且这个结点没有被访问过 if ($graphArr[$x][$y] != 0 && !$visited[$y]) { // 进行栈递归，传递的参数是当前这个结点 DFS_AM($graphArr, $y); } } } BuildGraph($graphArr); // 建立邻接矩阵图 echo '请输入开始遍历的结点（1-结点数）：'; fscanf(STDIN, "%d", $startNode); // 输入从第几个结点开始访问 DFS_AM($graphArr, $startNode); // 开始深度优先遍历

Die Menge an Code ist nicht groß. Ich verwende den Code zum Erstellen der Adjazenzmatrix im vorherigen Artikel. Wenn Sie ihn vergessen haben, schauen Sie noch einmal nach oder lesen Sie den Quellcode direkt über den Link unten der Artikel.

Als nächstes testen wir:

# php 5.3图的遍历：深度优先与广度优先.php 输入结点数：4 请输入边数：3 请输入边，格式为 出 入 权：1 2 1 请输入边，格式为 出 入 权：1 3 1 请输入边，格式为 出 入 权：3 4 1 请输入开始遍历的结点（1-结点数）：3 节点：3 节点：1 节点：2 节点：4

Adjazenzliste

Natürlich ist die Idee des Durchlaufens der Adjazenzliste dieselbe, außer dass der Schleifenalgorithmus in der Mitte die Kettencharakteristikmethode verwendet.

$visited = []; // 已访问结点 function DFS_AL($graph, $x){ global $visited; $p = $graph->adjList[$x]; // 指定结点的第一个边结点 echo "节点：{$x}", PHP_EOL; // 输出指定结点的信息 $visited[$x] = true; // 设置该结点已被访问 while($p != null){ $y = $p->adjVex; // 获得边结点信息 if(!$visited[$y]){ // 如果结点没有被访问过 DFS_AL($graph, $y); // 进入这个边结点的深度遍历过程 } $p = $p->nextArc; // 移动到下一个边结点 } } $graph = BuildLinkGraph(); $graphBFS = $graph; echo '请输入开始遍历的结点（1-结点数）：'; fscanf(STDIN, "%d", $startNode); // 输入从第几个结点开始访问 DFS_AL($graph, $startNode);// 开始深度优先遍历

Ist es auch ganz einfach? Als nächstes testen wir es einfach:

# php 5.3图的遍历：深度优先与广度优先.php 请输入 结点数 边数： 4 3 请输入边，格式为 出 入 权：1 2 1 请输入边，格式为 出 入 权：1 3 1 请输入边，格式为 出 入 权：3 4 1 请输入开始遍历的结点（1-结点数）：3 节点：3 节点：4 节点：1 节点：2

Warum unterscheidet sich die Ausgabereihenfolge von der Adjazenzmatrix? Die im vorherigen Artikel implementierte Adjazenzliste verwendet die Kopfinterpolation. Die späteren Eingabedaten werden vor der Knotenverknüpfung hinzugefügt. Wenn wir 3 4 1 in die erste Eingabe einfügen, ist der Knoten derselbe wie die Adjazenzmatrix Die Durchlaufergebnisse sind die gleichen.

Depth-First-Traversal-Symbol

Ich habe mir den Code direkt angesehen und lange über den Algorithmus gesprochen. Sind Sie immer noch verwirrt? Egal, schauen wir uns das Bild direkt an:

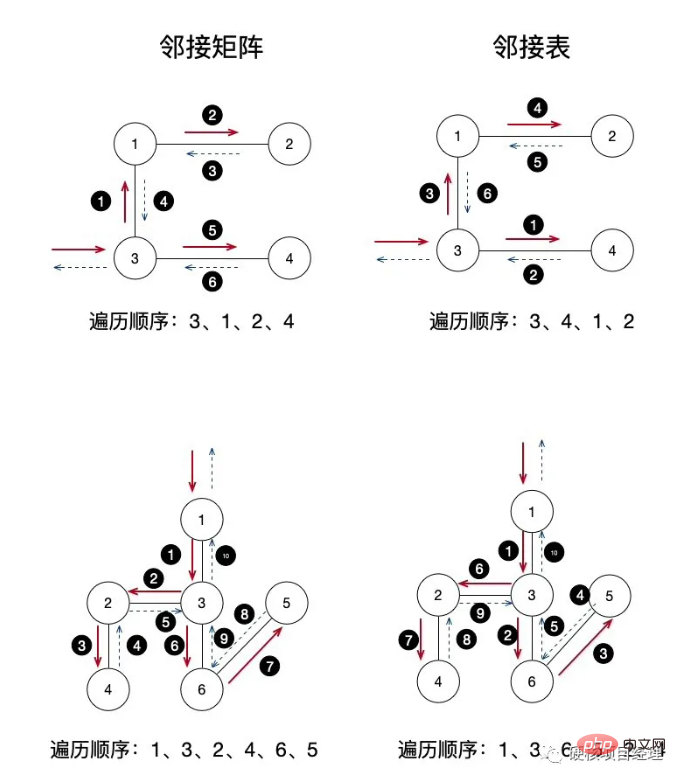
Die linke Seite ist die Adjazenzmatrix und die rechte Seite ist die Adjazenzliste. Der von uns getestete Graph ist relativ einfach, mit 4 Knoten und 3 Kanten. Der folgende ist ein komplexerer Graph mit 6 Knoten und 5 Kanten. Sie können es selbst testen. Sehen Sie sich die Zahlen in den kleinen schwarzen Kreisen an, um die Durchlauf- und Ausführungsreihenfolge jedes Schritts zu ermitteln. Lassen Sie uns anhand des ersten Bildes der Adjazenzmatrix kurz die Zugriffsschritte erläutern:

• Zuerst geben wir den Zugriff von Knoten 3 ein und starten dann die Tiefendurchquerung. Zu diesem Zeitpunkt ist der Ausgabeknoten 3

• Zuerst erhalten wir in der Schleife von Schritt Knoten 3, dass er eine Kante mit Knoten 1 hat, also übergeben wir Knoten 1 rekursiv und Knoten 1 wird auf den Stapel geschoben

• Ausgabeknoten 1. In der aktuellen Rekursion Knoten 1 liegt oben auf dem Stapel

• 在 结点1 的循环中发现 结点1 和 结点 2 有边，于是递归传入 结点2 ，结点2 入栈

• 输出 结点2，目前的递归中 结点2 在栈顶

• 注意了，重点在这里，结点2 的循环中没有发现与其它未访问的结点有边存在了，于是递归开始返回，也就是开始出栈了，依次返回到 结点1 、结点3，没有任何输出，栈空了，递归回到最外层的函数了

• 继续 结点3 的循环，发现与 结点4 有边，递归传入 结点4

• 输出 结点4，目前的递归中 结点4 在栈顶

• 结点4 的循环中没有发现其它未访问的结点及边了，递归返回，结点4 出栈

• 结点3 循环完成，遍历结束

一步一步的很清晰吧，大家试着自己分析一下下面那个复杂一些图的深度遍历顺序，看看和我们程序输出的结果是不是一样的。在很多的考研或者数据结构考试中，经常会有选择题或应用题让你手动地来写出深度优先遍历的顺序哦！

广度优先遍历

接下来就是广度优先遍历了，其实说白了就是我们在学习树的遍历时候的层序遍历。前面我们说过，深度遍历是一条路走到黑，没路了退回来。而广度遍历则是一层一层的查看，直到找到出口。

邻接矩阵

使用邻接矩阵来进行广度优先遍历的操作，其实最核心的遍历方式和深度遍历没什么区别，都是对某一个结点进行边的查找，唯一不同的就是把递归栈换成了队列而已。

$visited = []; function BFS_AM($graphArr, $x){ global $visited; $queue = InitSqQueue(); // 初始化队列 $graphCount = count($graphArr); // 获取矩阵结点数量 $visited[$x] = true; // 结点标记为已访问 EnSqQueue($queue, $x); // 结点入队 while($x){ // 循环判断结点是否 fasle // 遍历所有结点是否与这个结点有边 for ($y = 1; $y <= $graphCount; $y++) { // 如果有边并且未访问过 if ($graphArr[$x][$y] != 0 && !$visited[$y]) { $visited[$y] = true; // 结点标记为已访问 EnSqQueue($queue, $y); // 结点入队 } } $x = DeSqQueue($queue); // 出队一个结点 echo $x, PHP_EOL; // 输出结点 } } echo '请输入开始广度遍历的结点（1-结点数）：'; fscanf(STDIN, "%d", $startNode); BFS_AM($graphArr, $startNode); // 开始广度遍历

代码中的注释也很清晰明了了，我们直接进行测试：

…… …… 请输入开始广度遍历的结点（1-结点数）：3 3 1 4 2

邻接表

同样地，我们也提供邻接表的链式广度优先遍历的核心函数。

$visited = []; function BFS_AL($graph, $x){ global $visited; $visited[$x] = true; // 结点标记为已访问 $queue = InitSqQueue();// 初始化队列 EnSqQueue($queue, $x); // 结点入队 // 如果一直有能出队的结点，就一直循环 // 也就是说，如果队列空了，循环就结束 while(($i = DeSqQueue($queue))!==false){ echo $i, PHP_EOL; // 输出结点 $p = $graph->adjList[$i]; // 结点的第一个边结点 while($p != null){ // 如果不为空 $y = $p->adjVex; // 边结点信息 if(!$visited[$y]){ // 如果没有访问过 $visited[$y] = true; // 标记结点为已访问 EnSqQueue($queue, $y); // 入队结点 } $p = $p->nextArc; // 结点指针指向下一个 } } } echo '请输入开始遍历的结点（1-结点数）：'; fscanf(STDIN, "%d", $startNode); BFS_AL($graph, $startNode); // 开始广度遍历

核心的循环中的操作其实也和深度遍历没什么太大的区别，同样是换成了队列这种存储形式而已。

…… …… 请输入开始广度遍历的结点（1-结点数）：3 3 4 1 2

广度优先遍历图示

好吧，上面又罗列完了算法，接下来就是图示的时间了，相信还是一看图大家就马上能明白广度优先遍历的具体步骤了。

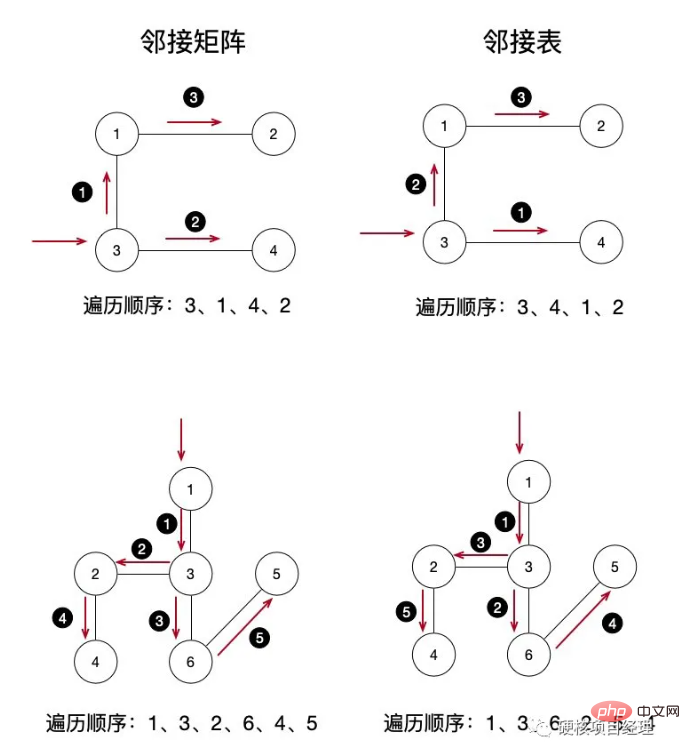
和上面的图一样，同样还是左边是邻接矩阵，右边是邻接表。在这里，我们依然还是直接分步骤来看一下左边最上面图的遍历操作顺序：

• 输入 结点3 开始广度遍历，结点标记为已访问，这时 结点3 入队

• 使用 while 循环判断 结点x 是否为 null ，如果不为 null 进入循环体

• 遍历所有结点是否与这个结点有边，如果有边，并且这个结点没有被访问过，标记已访问，加入队列

• 出队一个元素，并赋值给 x

• 输出 x 结点的信息

广度优先遍历没有栈的回溯，就是一条线性的队列走完就完了，所以图示会非常清晰。单独一个结点我们会将和它相关的所有结点入队，然后出队最顶上的结点，这样就能够像树的层序遍历一样按照一层一层的顺序来遍历整个图。同样地，拿起纸笔，找复杂一点的图，试试能不能手写出类似于广度优先遍历顺序的题目吧！

总结

大家学完了之后是不是发现今天介绍的深度优先和广度优先两种遍历方式真的和树的遍历方式没什么太大的区别。最大的不同就是我们要标记已访问过的结点而已。不管怎么说，使用栈和队列来对树或图进行遍历是所有树和图的操作算法中最最基础的部分，也是考试和面试中最常见的问题，大家一定要深入理解掌握哦！

测试代码： https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/5.图/source/5.3图的遍历：深度优先与广度优先.php

Das obige ist der detaillierte Inhalt vonPHP-Datenstruktur-Graph-Durchquerung: Tiefe zuerst und Breite zuerst. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!