Eine ausführliche Analyse der schnellen Sortierung in JavaScript

Einführung

Unter Sortieren versteht man das Anordnen der Elemente einer linearen Liste in einer bestimmten Reihenfolge (numerisch oder alphabetisch). Sortieren wird häufig in Verbindung mit der Suche verwendet.

Es gibt viele Sortieralgorithmen und einer der mit Abstand schnellsten ist Quicksort.

Quicksort sortiert die angegebenen Listenelemente mithilfe der Divide-and-Conquer-Strategie. Das bedeutet, dass der Algorithmus das Problem in Teilprobleme zerlegt, bis die Teilprobleme einfach genug sind, um direkt gelöst zu werden.

Algorithmisch kann dies durch Rekursion oder Schleife erreicht werden. Für dieses Problem ist es jedoch natürlicher, die Rekursion zu verwenden.

Verstehen Sie die Logik hinter der Schnellsortierung

Sehen Sie sich zunächst an, wie die Schnellsortierung funktioniert:

1. Wählen Sie ein Element im Array aus. Dieses Element heißt Pivot. Normalerweise wird das erste oder letzte Element im Array als Basis verwendet.
2. Anschließend ordnen Sie die Elemente des Arrays neu an, sodass alle Elemente links vom Pivot kleiner als der Pivot und alle Elemente rechts größer als der Pivot sind. Dieser Schritt wird Partition genannt. Wenn ein Element gleich der Basis ist, spielt es keine Rolle, auf welcher Seite es sich befindet.
3. Wiederholen Sie diesen Vorgang für die linke und rechte Seite des Benchmarks, bis das Array sortiert ist.

Als nächstes verstehen Sie diese Schritte anhand eines Beispiels. Angenommen, es gibt ein Array mit unsortierten Elementen [7, -2, 4, 1, 6, 5, 0, -4, 2]. Wählen Sie das letzte Element als Basis aus. Die Zerlegungsschritte des Arrays sind in der folgenden Abbildung dargestellt: [7, -2, 4, 1, 6, 5, 0, -4, 2] 的数组。选择最后一个元素作为基准。数组的分解步骤如下图所示：

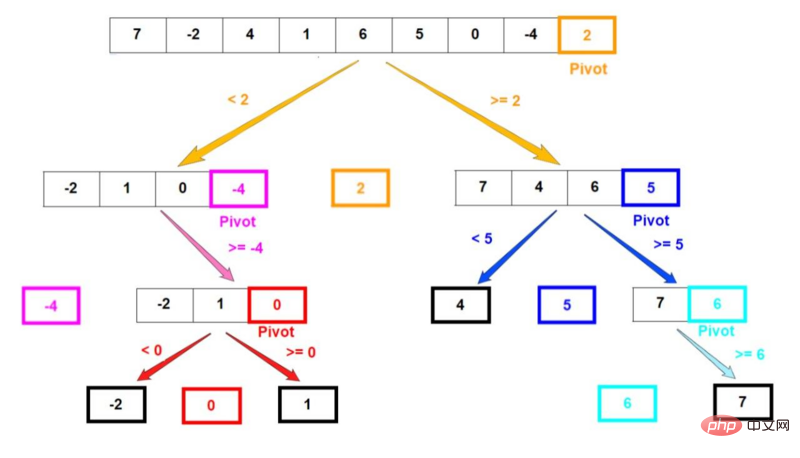
在算法的步骤1中被选为基准的元素带颜色。分区后，基准元素始终处于数组中的正确位置。

黑色粗体边框的数组表示该特定递归分支结束时的样子，最后得到的数组只包含一个元素。

最后可以看到该算法的结果排序。

用 JavaScript 实现快速排序

这一算法的主干是“分区”步骤。无论用递归还是循环的方法，这个步骤都是一样的。

正是因为这个特点，首先编写为数组分区的代码 partition()：

function partition(arr, start, end){
    // 以最后一个元素为基准
    const pivotValue = arr[end];
    let pivotIndex = start; 
    for (let i = start; i < end; i++) {
        if (arr[i] < pivotValue) {
        // 交换元素
        [arr[i], arr[pivotIndex]] = [arr[pivotIndex], arr[i]];
        // 移动到下一个元素
        pivotIndex++;
        }
    }
    
    // 把基准值放在中间
    [arr[pivotIndex], arr[end]] = [arr[end], arr[pivotIndex]] 
    return pivotIndex;
};

代码以最后一个元素为基准，用变量 pivotIndex 来跟踪“中间”位置，这个位置左侧的所有元素都比 pivotValue 小，而右侧的元素都比 pivotValue 大。

最后一步把基准（最后一个元素）与 pivotIndex 交换。

递归实现

在实现了 partition() 函数之后，我们必须递归地解决这个问题，并应用分区逻辑以完成其余步骤：

function quickSortRecursive(arr, start, end) {
    // 终止条件
    if (start >= end) {
        return;
    }
    
    // 返回 pivotIndex
    let index = partition(arr, start, end);
    
    // 将相同的逻辑递归地用于左右子数组
    quickSort(arr, start, index - 1);
    quickSort(arr, index + 1, end);
}

在这个函数中首先对数组进行分区，之后对左右两个子数组进行分区。只要这个函数收到一个不为空或有多个元素的数组，则将重复该过程。

空数组和仅包含一个元素的数组被视为已排序。

最后用下面的例子进行测试：

array = [7, -2, 4, 1, 6, 5, 0, -4, 2]
quickSortRecursive(array, 0, array.length - 1)

console.log(array)

输出：

-4,-2,0,1,2,4,5,6,7

循环实现

快速排序的递归方法更加直观。但是用循环实现快速排序是一个相对常见的面试题。

与大多数的递归到循环的转换方案一样，最先想到的是用栈来模拟递归调用。这样做可以重用一些我们熟悉的递归逻辑，并在循环中使用。

我们需要一种跟踪剩下的未排序子数组的方法。一种方法是简单地把“成对”的元素保留在堆栈中，用来表示给定未排序子数组的 start 和 end。

JavaScript 没有显式的栈数据结构，但是数组支持 push() 和 pop() 函数。但是不支持 peek()函数，所以必须用 stack [stack.length-1]

Genau aufgrund dieser Funktion wird der Code für die Array-Partitionierung zuerst partition() geschrieben:

function quickSortIterative(arr) {
    // 用push()和pop()函数创建一个将作为栈使用的数组
    stack = [];
    
    // 将整个初始数组做为“未排序的子数组”
    stack.push(0);
    stack.push(arr.length - 1);
    
    // 没有显式的peek()函数
    // 只要存在未排序的子数组，就重复循环
    while(stack[stack.length - 1] >= 0){
        
        // 提取顶部未排序的子数组
        end = stack.pop();
        start = stack.pop();
        
        pivotIndex = partition(arr, start, end);
        
        // 如果基准的左侧有未排序的元素，
        // 则将该子数组添加到栈中，以便稍后对其进行排序
        if (pivotIndex - 1 > start){
            stack.push(start);
            stack.push(pivotIndex - 1);
        }
        
        // 如果基准的右侧有未排序的元素，
        // 则将该子数组添加到栈中，以便稍后对其进行排序
        if (pivotIndex + 1 < end){
            stack.push(pivotIndex + 1);
            stack.push(end);
        }
    }
}

Der Code basiert auf dem letzten Element und verwendet die Variable pivotIndex</ code> um die „mittlere“ Position zu verfolgen. Alle Elemente auf der linken Seite dieser Position sind kleiner als <code>pivotValue und alle Elemente auf der rechten Seite sind größer als pivotValue.

Der letzte Schritt besteht darin, den Pivot (letztes Element) mit pivotIndex auszutauschen.

Rekursive Implementierung

Nach der Implementierung der Funktion partition() müssen wir das Problem rekursiv lösen und Partitionierungslogik anwenden, um die verbleibenden Schritte abzuschließen:

ourArray = [7, -2, 4, 1, 6, 5, 0, -4, 2]
quickSortIterative(ourArray)

console.log(ourArray)

In dieser Funktion zuerst Partitionieren Sie das Array und partitionieren Sie dann die linken und rechten Unterarrays. Solange diese Funktion ein Array empfängt, das nicht leer ist oder mehr als ein Element enthält, wird der Vorgang wiederholt.

-4,-2,0,1,2,4,5,6,7

Schleifenimplementierung

Es kann empirisch beobachtet werden, dass die Zeitkomplexität der schnellen Sortierung tendenziell $O(nlog n)$ beträgt, unabhängig davon, welche Daten-Benchmark-Auswahlstrategie angewendet wird.

Schnellsortierung nimmt keinen zusätzlichen Platz ein (mit Ausnahme des für rekursive Aufrufe reservierten Platzes). Dieser Algorithmus wird als „In-Place-Algorithmus“ bezeichnet und benötigt keinen zusätzlichen Speicherplatz. Weitere Kenntnisse zum Thema Programmierung finden Sie unter:

! !

Das obige ist der detaillierte Inhalt vonEine ausführliche Analyse der schnellen Sortierung in JavaScript. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!