
Der Inhalt dieses Artikels besteht darin, die Implementierung von Sortier- und Suchalgorithmen mit JS vorzustellen. Er hat einen gewissen Referenzwert. Ich hoffe, er wird für Sie hilfreich sein.
Bevor Sie sich mit dem Thema befassen, bereiten Sie einige Grundfunktionen vor
(1) Tauschen Sie zwei Elemente des Arrays aus
function swap(arr, sourceIndex, targetIndex) {
let temp = arr[sourceIndex];
arr[sourceIndex] = arr[targetIndex];
arr[targetIndex] = temp;
} (2) Generieren Sie schnell ein Array von 0~N
function createArr(length) {
return Array.from({length}, (_, i) => i);
}(3) Shuffle-Funktion
Die Zufallsfunktion kann das Array schnell durcheinander bringen.
function shuffle(arr) {
for (let i = 0; i <h2><strong>2. Sortierung</strong></h2><p>Übliche Sortieralgorithmen können in zwei Kategorien unterteilt werden : </p>O(nlogn) nicht überschreiten kann, wird sie auch als nichtlineare Zeitvergleichssortierung Kern: Vergleichen Sie zwei beliebige benachbarte Elemente und tauschen Sie sie aus, wenn das erste größer als das zweite ist . Die Elemente werden in der richtigen Reihenfolge nach oben verschoben, als würden Blasen an die Oberfläche steigen, daher der Name Blasensortierung
GIF:

Hinweis: Die erste Ebene wird durchlaufen, um den Maximalwert der verbleibenden Elemente zu ermitteln, und erreicht die angegebene Position [gibt nacheinander den Maximalwert aus]
Code:
function bubbleSort(arr) {
const len = arr.length;
for (let i = 0; i arr[j + 1]) { // 比较相邻元素
swap(arr, j, j + 1);
}
}
}
return arr;
}Kern: Suchen Sie zuerst das kleinste Element in der unsortierten Sequenz und speichern Sie es an der Startposition der sortierten Sequenz. Suchen Sie dann weiterhin das kleinste Element aus den verbleibenden unsortierten Elementen und fügen Sie es in die ein sortierte Reihenfolge. Und so weiter, bis alle Elemente sortiert sind
Gif:
Hinweis: Traversalfunde der ersten Ebene den Index des Mindestwerts der verbleibenden Elemente und tauscht dann die aktuelle Position und den Mindestindexwert aus [finden Sie nacheinander den Mindestwert]
Code:
function selectionSort(arr) {
const len = arr.length;
let minIndex;
for (let i = 0; i arr[j]) {
minIndex = j; // 寻找最小值对应的索引
}
}
if (minIndex === i) continue;
swap(arr, minIndex, i);
}
return arr;
}Kern: Durch Erstellen einer geordneten Sequenz scannen Sie bei unsortierten Daten die sortierte Sequenz von hinten nach vorne, suchen Sie die entsprechende Position und fügen Sie
GIF ein :
Hinweis: Vergleichen Sie ab dem zweiten Element vorwärts, um sicherzustellen, dass die vorherige Reihenfolge des aktuellen Elements in der richtigen Reihenfolge ist
Code:
function insertionSort(arr) {
const len = arr.length;
let current, pointer;
for (let i = 1; i = 0 && current <h3>2.4 Zusammenführungssortierung<strong></strong>
</h3> Im Vergleich zu den oben genannten drei Sortieralgorithmen sind Zusammenführungssortierung und Schnellsortierung praktischer in der Praxis ist praktikabler (im vierten Abschnitt vergleichen wir diese Sortieralgorithmen anhand praktischer Komplexität) Die <p>-Klasse von </p><blockquote>
<code>JavaScript</code> definiert eine <code>Array</code>-Funktion (<code>sort</code>) Wird verwendet um das Array <code>Array.prototype.sort</code> zu sortieren. <code>JavaScript</code>Es gibt keine Definition, welcher Sortieralgorithmus verwendet wird, daher können Browserhersteller den Algorithmus selbst implementieren. Beispielsweise verwendet <code>ECMAScript</code> <code>Mozilla Firefox</code>merge sort<strong> als Implementierung von </strong>, während <code>Array.prototype.sort</code> eine Variante von <code>Chrome</code>quicksort<strong> verwendet </strong>
</blockquote><p>merge sort Es ist eine Art <strong>. Die Idee besteht darin, das ursprüngliche Array in kleinere Arrays aufzuteilen, bis jedes kleine Array nur noch eine Position hat, und dann die kleinen Arrays zu größeren Arrays zusammenzuführen, bis nur noch ein sortiertes großes Array vorhanden ist. Daher müssen Sie den <code>分治算法</code><code>递归</code></strong></p><p>-Kern verwenden: Sortierung zusammenführen, in linke und rechte Arrays aufteilen, separat sortieren und dann <strong></strong></p>Animation:<p style="text-align: left;"><strong></strong></p><p style="text-align: center;"></p><p><strong>注意:递归中最小的左右数组比较为单个元素的数组,因此在较上层多个元素对比时,左右两个数组一定是顺序的</strong></p><p><strong>代码:</strong></p><pre class="brush:php;toolbar:false">function mergeSort(arr) {
const len = arr.length;
if (len right[0]) {
ret.push(right.shift());
} else {
ret.push(left.shift());
}
}
while (left.length) {
ret.push(left.shift());
}
while (right.length) {
ret.push(right.shift());
}
return ret;
}快速排序也许是最常用的排序算法了。它的复杂度为O(nlogn),且它的性能通常比其他的复 杂度为O(nlogn)的排序算法要好。和归并排序一样,快速排序也使用分治的方法,将原始数组分为较小的数组
核心:分治算法,以参考值为界限,将比它小的和大的值拆开
动图:
注意:每一次遍历筛选出比基准点小的值
代码:
function quickSort(arr, left = 0, right = arr.length - 1) {
// left和right默认为数组首尾
if (left <h2><strong>三、搜索算法</strong></h2><h3><strong>3.1 顺序搜索</strong></h3><p>顺序或线性搜索是最基本的搜索算法。它的机制是,将每一个数据结构中的元素和我们要找的元素做比较。<strong>顺序搜索是最低效的一种搜索算法。</strong></p><pre class="brush:php;toolbar:false">function findItem(item, arr) {
for (let i = 0; i <h3><strong>3.2 二分搜索</strong></h3><p>二分搜索要求被搜索的数据结构已排序。以下是该算法遵循的步骤:</p><ol>
<li>选择数组的中间值</li>
<li>如果选中值是待搜索值,那么算法执行完毕</li>
<li>如果待搜索值比选中值要小,则返回步骤1在选中值左边的子数组中寻找</li>
<li>如果待搜索值比选中值要大,则返回步骤1在选中值右边的子数组中寻找</li>
</ol><pre class="brush:php;toolbar:false">function binarySearch(item, arr) {
arr = quickSort(arr); // 排序
let low = 0;
let high = arr.length - 1;
let mid;
while (low item) {
high = mid - 1;
} else {
return mid;
}
}
return -1;
}大O表示法用于描述算法的性能和复杂程度。分析算法时,时常遇到一下几类函数
(1)O(1)
function increment(num){
return ++num;
}执行时间和参数无关。因此说,上述函数的复杂度是O(1)(常数)
(2)O(n)
以顺序搜索函数为例,查找元素需要遍历整个数组,直到找到该元素停止。函数执行的总开销取决于数组元素的个数(数组大小),而且也和搜索的值有关。但是函数复杂度取决于最坏的情况:如果数组大小是10,开销就是10;如果数组大小是1000,开销就是1000。这种函数的时间复杂度是O(n),n是(输入)数组的大小
(3)O(n2)
以冒泡排序为例,在未优化的情况下,每次排序均需进行n*n次执行。时间复杂度为O(n2)
时间复杂度O(n)的代码只有一层循环,而O(n2)的代码有双层嵌套循环。如 果算法有三层遍历数组的嵌套循环,它的时间复杂度很可能就是O(n3)
(1)常用数据结构时间复杂度
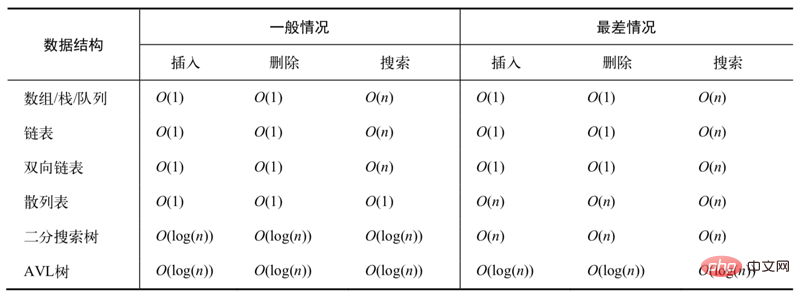
(2)排序算法时间复杂度
相关视频教程推荐:《JavaScript教程》
以上就是本篇文章的全部内容,希望能对大家的学习有所帮助。更多精彩内容大家可以关注php中文网相关教程栏目!!!
Das obige ist der detaillierte Inhalt vonSo implementieren Sie Sortier- und Suchalgorithmen in JS. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!