Detaillierte Erläuterung des Javascript-Trie-Präfixbaumcodes-js-Tutorial-php.cn

Dieser Artikel stellt hauptsächlich Beispiele für JavaScript-Trie-Wortsuchbäume vor. Er hat einen gewissen Referenzwert und kann jedem helfen.

Einführung

Der Trie-Baum (aus dem Wort „Retrieval“), auch Präfixwort, Wortsuchbaum, Wörterbuchbaum genannt, ist eine Baumstruktur, eine haha-Variante des griechischen Baums, einer Struktur aus mehreren Bäumen, die zum schnellen Auffinden verwendet wird.

Seine Vorteile sind: Minimierung unnötiger Zeichenfolgenvergleiche und eine höhere Abfrageeffizienz als bei Hash-Tabellen.

Die Kernidee von Trie ist der Austausch von Raum gegen Zeit. Verwenden Sie das gemeinsame Präfix von Zeichenfolgen, um den Zeitaufwand für Abfragen zu reduzieren und die Effizienz zu verbessern.

Der Trie-Baum hat auch seine Mängel. Unter der Annahme, dass wir nur Buchstaben und Zahlen verarbeiten, hat jeder Knoten mindestens 52+10 untergeordnete Knoten. Um Speicherplatz zu sparen, können wir verknüpfte Listen oder Arrays verwenden. In JS verwenden wir Arrays direkt, da JS-Arrays dynamisch sind und über eine integrierte Optimierung verfügen.

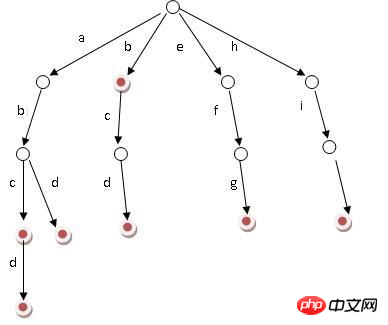
Grundlegende Eigenschaften

Der Wurzelknoten enthält keine Zeichen und jeder untergeordnete Knoten außer dem Wurzelknoten enthält ein Zeichen
Vom Wurzelknoten zu einem bestimmten Knoten. Die auf dem Pfad übergebenen Zeichen sind verbunden, was die Zeichenfolge ist, die dem Knoten entspricht
Alle Unterknoten jedes Knotens enthalten unterschiedliche Zeichen

Programmimplementierung

// by 司徒正美
class Trie {
 constructor() {
  this.root = new TrieNode();
 }
 isValid(str) {
  return /^[a-z1-9]+$/i.test(str);
 }
 insert(word) {
  // addWord
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    var node = cur.son[c];
    if (node == null) {
     var node = (cur.son[c] = new TrieNode());
     node.value = word.charAt(i);
     node.numPass = 1; //有N个字符串经过它
    } else {
     node.numPass++;
    }
    cur = node;
   }
   cur.isEnd = true; //樯记有字符串到此节点已经结束
   cur.numEnd++; //这个字符串重复次数

   return true;
  } else {
   return false;
  }
 }
 remove(word){
   if (this.isValid(word)) {
     var cur = this.root;
     var array = [], n = word.length
     for (var i = 0; i < n; i++) {
       var c = word.charCodeAt(i);
       c = this.getIndex(c)
       var node = cur.son[c];
       if(node){
         array.push(node)
         cur = node
       }else{
         return false
       }
 
     }
     if(array.length === n){
       array.forEach(function(){
         el.numPass--
       })
       cur.numEnd --
       if( cur.numEnd == 0){
         cur.isEnd = false
       } 
     }
   }else{
     return false
   }
 }
 preTraversal(cb){//先序遍历
    function preTraversalImpl(root, str, cb){ 
      cb(root, str);
      for(let i = 0,n = root.son.length; i < n; i ++){
        let node = root.son[i];
        if(node){
          preTraversalImpl(node, str + node.value, cb);
        }
      }
    } 
    preTraversalImpl(this.root, "", cb);
  }
 // 在字典树中查找是否存在某字符串为前缀开头的字符串(包括前缀字符串本身)
 isContainPrefix(word) {
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return false;
    }
   }
   return true;
  } else {
   return false;
  }
 }
 isContainWord(str) {
  // 在字典树中查找是否存在某字符串(不为前缀)
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return false;
    }
   }
   return cur.isEnd;
  } else {
   return false;
  }
 }
 countPrefix(word) {
  // 统计以指定字符串为前缀的字符串数量
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return 0;
    }
   }
   return cur.numPass;
  } else {
   return 0;
  }
 }
 countWord(word) {
  // 统计某字符串出现的次数方法
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return 0;
    }
   }
   return cur.numEnd;
  } else {
   return 0;
  }
 }
}

class TrieNode {
 constructor() {
  this.numPass = 0;//有多少个单词经过这节点
  this.numEnd = 0; //有多少个单词就此结束
  this.son = [];
  this.value = ""; //value为单个字符
  this.isEnd = false;
 }
}

Nach dem Login kopieren

Konzentrieren wir uns auf die Einfügemethode von TrieNode und Trie. Da der Wörterbuchbaum hauptsächlich für die Worthäufigkeitsstatistik verwendet wird, verfügt er über viele Knotenattribute, einschließlich numPass und numEnd, aber sehr wichtige Attribute.

Die Einfügemethode wird zum Einfügen schwerer Wörter verwendet. Bevor wir beginnen, müssen wir feststellen, ob das Wort zulässig ist. Sonderzeichen und Leerzeichen dürfen nicht vorkommen. Beim Einfügen werden Zeichen aufgebrochen und in jedem Knoten platziert. numPass muss jedes Mal geändert werden, wenn ein Knoten übergeben wird.

Optimierung

Jetzt gibt es in jeder unserer Methoden eine Operation von c=-48. Tatsächlich gibt es andere Zeichen zwischen Zahlen, Großbuchstaben und Kleinbuchstaben Dies führt zu unnötiger Platzverschwendung

// by 司徒正美
getIndex(c){
   if(c < 58){//48-57
     return c - 48
   }else if(c < 91){//65-90
     return c - 65 + 11
   }else {//> 97 
     return c - 97 + 26+ 11
   }
 }

Nach dem Login kopieren

Dann besteht die relevante Methode darin, c-= 48 in c = this.getIndex(c)

Test

var trie = new Trie(); 
  trie.insert("I"); 
  trie.insert("Love"); 
  trie.insert("China"); 
  trie.insert("China"); 
  trie.insert("China"); 
  trie.insert("China"); 
  trie.insert("China"); 
  trie.insert("xiaoliang"); 
  trie.insert("xiaoliang"); 
  trie.insert("man"); 
  trie.insert("handsome"); 
  trie.insert("love"); 
  trie.insert("Chinaha"); 
  trie.insert("her"); 
  trie.insert("know"); 
  var map = {}
  trie.preTraversal(function(node, str){
    if(node.isEnd){
     map[str] = node.numEnd
    }
  })
  for(var i in map){
    console.log(i+" 出现了"+ map[i]+" 次")
  }
  console.log("包含Chin（包括本身）前缀的单词及出现次数："); 
  //console.log("China")
  var map = {}
  trie.preTraversal(function(node, str){
    if(str.indexOf("Chin") === 0 && node.isEnd){
      map[str] = node.numEnd
    }
   })
  for(var i in map){
    console.log(i+" 出现了"+ map[i]+" 次")
  }

Nach dem Login kopieren

Vergleich von Trie-Baum und anderen Datenstrukturen

Trie-Baum und binärer Suchbaum

Der binäre Suchbaum sollte die früheste Baumstruktur sein, mit der wir in Berührung kommen, wenn die Datengröße n ist EinfügungenDie zeitliche Komplexität von Such- und Löschvorgängen beträgt normalerweise nur O (log n). Im schlimmsten Fall haben alle Knoten im gesamten Baum nur einen untergeordneten Knoten, der zu einer linearen Tabelle degeneriert der Einfügungs-, Such- und Löschoperationen ist komplex. Der Grad ist O(n).

Normalerweise ist die Höhe n des Trie-Baums viel größer als die Länge m der Suchzeichenfolge, sodass die zeitliche Komplexität des Suchvorgangs normalerweise O (m) und im schlimmsten Fall die zeitliche Komplexität beträgt ist O(n). Es ist leicht zu erkennen, dass die Worst-Case-Suche in einem Trie-Baum schneller ist als ein binärer Suchbaum.

Der Trie-Baum in diesem Artikel verwendet eine Zeichenfolge als Beispiel. Tatsächlich gelten strenge Anforderungen an die Eignung des Schlüssels. Wenn der Schlüssel eine Gleitkommazahl ist, kann der gesamte Trie-Baum extrem lang sein Die Lesbarkeit der Knoten ist ebenfalls sehr schlecht. In diesem Fall ist die Verwendung des Trie-Baums zum Speichern von Daten nicht geeignet.

Trie-Baum und Hash-Tabelle

Betrachten Sie das Problem des Hash-Konflikts. Wir sagen normalerweise, dass die Komplexität einer Hash-Tabelle O(1) ist. Genau genommen ist dies die Komplexität einer Hash-Tabelle, die nahezu perfekt ist. Darüber hinaus müssen wir auch berücksichtigen, dass die Hash-Funktion selbst benötigt wird um die Suchzeichenfolge zu durchlaufen, und die Komplexität beträgt O(m). Wenn unterschiedliche Schlüssel der „gleichen Position“ zugeordnet werden (unter Berücksichtigung des geschlossenen Hashings kann diese „gleiche Position“ durch eine gewöhnliche verknüpfte Liste ersetzt werden), hängt die Komplexität der Suche von der Anzahl der Knoten unter der Nummer „gleiche Position“ ab. Daher kann die Hash-Tabelle im schlimmsten Fall auch zu einer einseitig verknüpften Liste werden.

Trie-Bäume können einfacher nach der alphabetischen Reihenfolge der Schlüssel sortiert werden (der gesamte Baum wird einmal der Reihe nach durchlaufen), was sich von den meisten Hash-Tabellen unterscheidet (Hash-Tabellen haben im Allgemeinen unterschiedliche Schlüssel für unterschiedliche Schlüssel). ist ungeordnet).

Unter idealen Umständen kann die Hash-Tabelle das Ziel schnell mit O(1)-Geschwindigkeit erreichen. Wenn diese Tabelle sehr groß ist und auf der Festplatte platziert werden muss, ist der Suchzugriff der Hash-Tabelle schneller Im Idealfall muss dies nur einmal erfolgen; die Anzahl der Festplattenzugriffe durch den Trie-Baum muss jedoch der Knotentiefe entsprechen.

Oft benötigt ein Trie-Baum mehr Platz als eine Hash-Tabelle. Wenn wir die Situation betrachten, in der ein Knoten ein Zeichen speichert, gibt es beim Speichern einer Zeichenfolge keine Möglichkeit, es als separaten Block zu speichern. Durch die Knotenkomprimierung des Trie-Baums kann dieses Problem erheblich gemildert werden, worauf später noch eingegangen wird.

Verbesserung des Trie-Baums

Bitwise Trie (Bitwise Trie)

Im Prinzip ähnelt es dem gewöhnlichen Trie-Baum, mit der Ausnahme, dass es sich um einen gewöhnlichen Trie-Baum handelt Trie-Baum speichert Die kleinste Einheit ist ein Zeichen, aber Bitwise Trie speichert nur Bits. Der Zugriff auf Bitdaten wird einmal direkt durch den CPU-Befehl implementiert. Bei Binärdaten ist dies theoretisch schneller als beim gewöhnlichen Trie-Baum.

Knotenkomprimierung.

Zweigkomprimierung: Für einen stabilen Trie-Baum werden grundsätzlich Such- und Lesevorgänge ausgeführt, und einige Zweige können komprimiert werden. Beispielsweise kann das Inn des Zweigs ganz rechts in der vorherigen Abbildung direkt in einen Knoten „inn“ komprimiert werden, ohne als regulärer Teilbaum zu existieren. Der Radix-Baum basiert auf diesem Prinzip, um das Problem zu lösen, dass der Trie-Baum zu tief ist.

Knotenzuordnungstabelle: Diese Methode wird auch verwendet, wenn die Knoten des Trie-Baums möglicherweise fast vollständig für jeden Zustand des Knotens im Trie-Baum bestimmt wurden, wenn die Gesamtzahl der Zustände viele Male wiederholt wird Durch ein Element, das als mehrdimensionales Array von Zahlen dargestellt wird (z. B. Triple Array Trie), wird der Platzaufwand für die Speicherung des Trie-Baums selbst geringer, obwohl eine zusätzliche Zuordnungstabelle eingeführt wird.

Anwendung des Präfixbaums

Der Präfixbaum ist immer noch leicht zu verstehen und seine Anwendung ist auch sehr breit.

(1) Schnelles Abrufen von Zeichenfolgen

Die Abfragezeitkomplexität des Wörterbuchbaums beträgt O(logL), wobei L die Länge der Zeichenfolge ist. Der Wirkungsgrad ist also immer noch relativ hoch. Wörterbuchbäume sind effizienter als Hashtabellen.

(2) String-Sortierung

Aus der obigen Abbildung können wir leicht erkennen, dass die Wörter sortiert sind und zuerst die alphabetische Reihenfolge durchlaufen wird. Reduzieren Sie unnötige gemeinsame Teilzeichenfolgen.

(3) Das längste gemeinsame Präfix

Das längste gemeinsame Präfix von inn und int ist in. Beim Durchlaufen des Wörterbuchbaums zum Buchstaben n ist das gemeinsame Präfix dieser Wörter in.

(4) Präfixe automatisch abgleichen und Suffixe anzeigen

Wenn wir ein Wörterbuch oder eine Suchmaschine verwenden, geben Sie appl ein, und eine Menge Dinge mit dem Präfix appl werden automatisch angezeigt. Dann kann dies über einen Wörterbuchbaum erreicht werden. Wie bereits erwähnt, müssen wir nur die verbleibenden Suffixe durchqueren und anzeigen.

Verwandte Empfehlungen:

Über uery EasyUI kombiniert mit ztrIees Hintergrund-Seitenentwicklungs-Tutorial

Über Wörterbuchbaum-Trie in PHP-Beispiel der Implementierungsdefinitionsmethode

Word PHP implementiert Trie-Baum (Wörterbuchbaum)

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung des Javascript-Trie-Präfixbaumcodes. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!