
Hinweis: Da die Untersuchung des „Teilmengensummenproblems“ nicht ausführlich genug ist, kann es sein, dass dieser Artikel unklare Beschreibungen oder Fehler bei der Erklärung der dynamischen Programmierrekursionsformel enthält. Wenn Sie welche finden, hoffe ich Du kannst nicht zögern, es mir beizubringen.
Das Teilmengensummenproblem kann wie folgt beschrieben werden: Gegeben sind n positive ganze Zahlen W=(w1, w2, …, wn) und die positive ganze Zahl M erforderlich so Eine TeilmengeI⊆{1, 2, 3, ..., n},so dass∑wi=M,i∈I[1] . Nehmen Sie ein Beispiel, um eine beliebte Erklärung des Teilmengensummenproblems zu geben: Setze W=(1, 2, 3, 4, 5), gegeben eine positive ganze Zahl M = 5, gibt es eine Teilmenge I von W, so dass die Teilmenge Die Summe der Elemente in I ist gleich M. In diesem Beispiel gibt es offensichtlich eine Teilmenge I=(2, 3).
Problemdefinition: Die Menge der positiven ganzen ZahlenS=(w1, w2, w3, …, wn), gegeben positive Ganzzahl W, s[i, j] in i bedeutet S ist eine Teilmenge und j stellt die Summe der Teilmengen i dar. Wenn die Summe der Elemente S einer Menge i j=M ist Das heißt, das Problem hat eine Lösung.
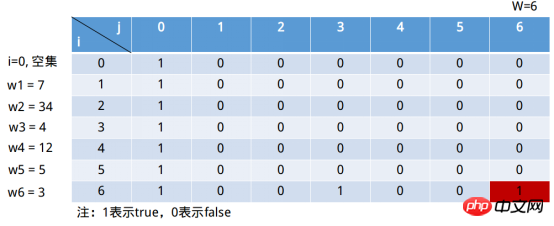
Beispiel:S=(7, 34, 4, 12, 5, 3), W=6, ob es eine Teilmenge von S gibt, die Summe ihrer Elemente ist gleich W.
Es gibt auch viele Lösungen für dieses Problem. In diesem Artikel wird die Idee der dynamischen Programmierung zur Lösung verwendet, dann muss eine rekursive Formel abgeleitet werden. Wir teilen die MengeS kontinuierlich in kleine Mengen auf. Dies ist der erste Schritt der dynamischen Programmierung: Definition des Teilproblems . Die kleinste Menge der Menge S ist die leere Menge. Natürlich existiert die leere Menge nicht. Die Summe ihrer Elemente ist gleich W. Wenn j=0 ist, ist natürlich die leere Menge zulässig.
Die Spalten dieser Tabelle stellen die Summe der Elemente in der Menge dar. Sie kann höchstens das Element W erreichen. Es ist natürlich bedeutungslos, wenn es größer als ist W . Solange 1 in der Spalte j=6 erscheint, liegt die Lösung des Problems vor. Die Zeile stellt eine Teilmenge dar, die aus den ersten i (einschließlich i) Elementen besteht (dieser Satz mag etwas zweifelhaft sein, nicht wahr?) Sie können nicht alles scannen? i=0 stellt die leere Menge dar. Wenn wir j=6 definieren, ist die leere Mengensituation wahr. Wenn dann j=0 ist, gilt dies für jede Teilmengensumme (die leere Menge ist ihre Teilmenge). Das Formular füllt sich also weiterhin wie unten gezeigt. Dies ist eigentlich der dritte Schritt der dynamischen Programmierung: Definieren Sie den Anfangszustand. Der zweite Schritt der Zustandsplanung besteht darin, Zustandsübergangsregeln zu definieren, also die rekursive Beziehung zwischen Staaten. Das i in s[i, j] stellt das erste i dar Teilmenge ( enthält i). Tatsächlich teilen wir es von hier aus in zwei Teile auf: 1) Ohne das erste ii-Elements 🎜> Teilmenge, das heißt s[i - 1, j]; i Die erste i Teilmenge von Elementen. Für den Fall Schwer zu verstehen ist die 2)Situation. Eine Sache, die über den zweiten Fall klargestellt werden kann, ist, dass i in s[i, X] sicher ist, und das Schlüssel ist j, j Wie definiert man es zu diesem Zeitpunkt? Nehmen Sie unter Verwendung der „Sonderwertmethode“ in der Mathematik den Beispielsatz (3, 34, 9 ), gibt es eine gegebene Teilmenge, deren Summe der Elemente gleich 37 ist, zu diesem Zeitpunkt i=2 (Teilmenge ist (3, 34)), j = 37, zu diesem Zeitpunkt “ Einschließlich der ersten i Teilmenge " des i Element Im Fall s[2, 37] => s[2, 37 - 34] = s[2, 3], Teilmenge (3 , 34) Natürlich gibt es eine Teilmenge, deren Summe der Elemente gleich 3 ist. Wenn dann j = 36, s[2, 36] => >, die Teilmenge (3, 34) existiert offensichtlich nicht und die Summe ihrer Teilmengenelemente ist gleich 2. Was ist mit j = 1, s[2, 1] => s[2, 1 - 34] = s[2, -32], j - wi < 0, zu diesem Zeitpunkt s[2, 1] => ] = s[1, 1], Teilmenge (3) Offensichtlich gibt es keine Teilmenge, deren Summe der Elemente gleich 1 ist . Die Teilmenge zu diesem Zeitpunkt ist (7), j = 1 , j ∉ (∅), Auswahlbedingung 2) => s[0, 1] || s[1, -6] (i = 0 stellt die leere Menge dar). Offensichtlich s[1, 1] = 0. ②i = 1, Die Teilmenge zu diesem Zeitpunkt ist (7), j = 2, j ∉ (∅) , Auswahlsituation 2) => s[0, 2] || s[1, -5](i = 0 stellt die leere Menge dar). Offensichtlich s[1, 2] = 0. … ⑥i = 1, zu diesem Zeitpunkt ist die Teilmenge (7), j = 6, j ∉ (∅), Auswahlbedingung 2) => s[0, 6] || , -1] (i = 0 stellt die leere Menge dar). Offensichtlich s[1, 6] = 0. Die endgültige Füllung ist wie unten gezeigt: Weiter füllen in der letzten Zeile: ①i = 6, Die Teilmenge zu diesem Zeitpunkt ist (7, 34, 4, 12, 5, 3) , j = 1, j ∉ (7, 34, 4, 12, 5), Auswahlsituation 2) => ; s[5, 1] || s[6, -2] (i = 0 stellt die leere Menge dar) . Offensichtlich s[6, 1] = 0. ②i = 6, Die Teilmenge zu diesem Zeitpunkt ist (7, 34, 4, 12, 5, 3), j = 2, j ∉ (7, 34, 4, 12, 5), Auswahlsituation 2) => , 1] ||. s[6, -1] (i = 0 stellt die leere Menge dar). Offensichtlich s[6, 2] = 0. ③i = 6, Die Teilmenge zu diesem Zeitpunkt ist (7, 34, 4, 12, 5, 3), j = 3, j ∉ (7, 34, 4, 12, 5), Auswahlfall 2) => |. |. s[6, 0]. Offensichtlich s[6, 3] = 1. ... ⑥i = 6, Die Teilmenge zu diesem Zeitpunkt ist (7, 34, 4, 12, 5 , 3), j = 6, j ∉ (7, 34, 4, 12, 5), Auswahlsituation 2) => 🎜 >. Offensichtlich s[6, 6] = 1. Java Python3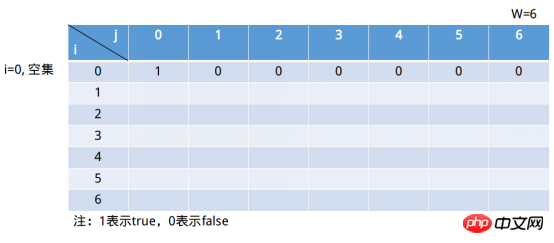
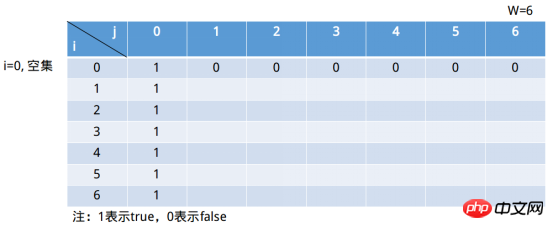
1) ist es einfacher zu verstehen, dass die Summe der ersten i - 1 Mengenelemente gleich ist zu j, dann ist die Summe der ersten i Mengenelemente gleich j . 
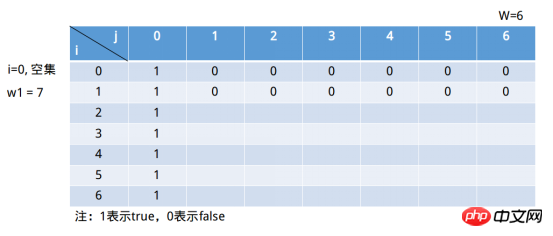
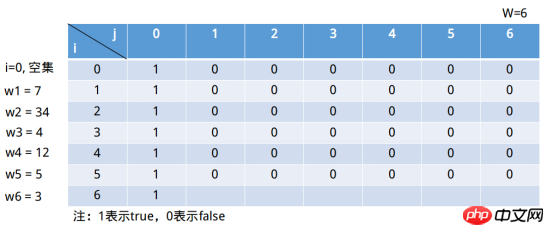
1 def subset_sum_problem(sets, sum): 2 row = len(sets) + 1 3 col = sum + 1 4 solutionMatrix = [[0 for col in range(col)] for row in range(row)] 5 solutionMatrix[0][0] = 1 6 for i in range(1, col): 7 solutionMatrix[0][i] = 0 8 9 for j in range(1, row):10 solutionMatrix[j][0] = 111 for k in range(1, col):12 solutionMatrix[j][k] = solutionMatrix[j - 1][k]13 if solutionMatrix[j][k] == 1:14 solutionMatrix[j][k] = solutionMatrix[j][k]15 elif (k - sets[j - 1] >= 0) and (solutionMatrix[j][k - sets[j - 1]] == 1):16 solutionMatrix[j][k] = solutionMatrix[j][k - sets[j - 1]]17 else:18 solutionMatrix[j][k] = 019 if k == col - 1 and solutionMatrix[j][k] == 1:20 return True21 22 return False23 24 sets = [7, 34, 4, 12, 5, 3]25 num = 626 is_exist = subset_sum_problem(sets, num)27 print(is_exist)
Das obige ist der detaillierte Inhalt vonDetaillierte Beispiele für Teilmengensummenprobleme. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




