HTML5 Advanced Programming Graphic Distortion und seine Anwendung 3 (erweitert)

Dieser Artikel ist der dritte in dieser Artikelserie. Die ersten beiden Artikel stellen das Prinzip der Erzielung eines Bildverzerrungseffekts in HTML5 sowie die detaillierte Verwendung der Drawtriangles-Funktion vor,

Werfen wir einen Blick auf die Erweiterung der Funktion „Drawtriangles“. Verwenden Sie die Funktion „Drawtriangles“, um eine rotierende 3D-Erde zu erstellen. Der Effekt ist wie folgt

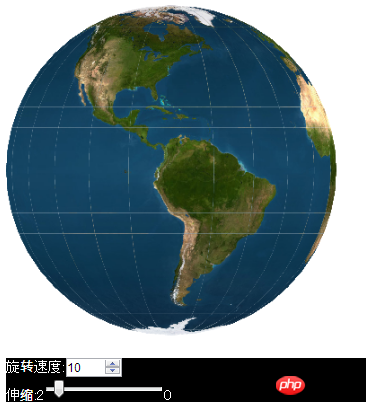
Da es einen Fehler in der Drawtriangles-Funktion von lufylegend Version 1.5.0 gibt, habe ich stillschweigend die lufylegend-Version 1.5.1 aktualisiert. Sie können sie unten von der offiziellen Website herunterladen Adresse:

http://lufylegend.com/lufylegend

Um den 3D-Kugeleffekt zu zeichnen, zeichnen Sie tatsächlich zuerst eine Ebene, teilen Sie die Ebene dann in kleine Dreiecke und verwenden Sie diese dann kleine Dreiecke, um eine Kugel zusammenzusetzen

Jetzt erstelle ich zuerst ein leeres LBitmapData-Objekt und teile dieses Objekt dann in N kleine Dreiecke. Weitere Informationen finden Sie im folgenden Code.

earthBitmapData = new LBitmapData("#ffffff", 0, 0, 500, 300);
var i, j;
vertices = new Array();
for(i=0;i<=cols;i++){
	for(j=0;j<=rows;j++){
		vertices.push(i*15,j*15);
	}
}
indices = new Array();
for (i = 0; i < cols; i++) {
	for (j = 0; j < rows; j++) {
		indices.push(i * (rows + 1) + j, (i + 1) * (rows + 1) + j, i * (rows + 1) + j + 1);
		indices.push((i + 1) * (rows + 1) + j, i * (rows + 1) + j + 1, (i + 1) * (rows + 1) + j + 1);
	}
}
uvtData = new Array();
for (i = 0; i <= cols; i++) {
	for (j = 0; j <= rows; j++) {
		uvtData.push(i / cols, j / rows);
	}
}

Verwenden Sie dann die Funktion „Drawtriangles“, um die LBitmapData zu teilen. Das Objekt wird auf den Bildschirm gezeichnet

backLayer = new LSprite();
addChild(backLayer);
backLayer.graphics.clear();
backLayer.graphics.beginBitmapFill(earthBitmapData);
backLayer.graphics.drawTriangles(vertices, indices, uvtData, 2);

und der Effekt ist wie unten gezeigt.

Wenn Sie diese Ebene in einen Kreis programmieren möchten, müssen Sie die Koordinaten jedes kleinen Dreiecks im Bild berechnen. Schauen wir uns zunächst an, wie das y Die Koordinate sollte berechnet werden. Siehe Das Bild unten ist ein vertikaler Abschnitt einer Kugel

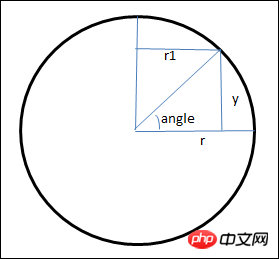
Verwenden Sie trigonometrische Funktionen, um die y-Koordinate im Bild und den horizontalen Abschnitt von zu berechnen der Ball an der Stelle der y-Koordinate wurde noch nicht berechnet, eine spezielle Figur wird wie folgt erhalten

var a = Math.sin(angle);
if((90-180*j/rows)%90==0 && (90-180*j/rows)%180!=0)a=(90-180*j/rows)>0?1:-1;
var y =  -r*a;
var sa = Math.cos(angle);
var r1 =  Math.abs(r*sa);

for(i=0;i<=cols;i++){
	for(j=0;j<=rows;j++){
		var angle = (90-180*j/rows)*Math.PI/180;
		var a = Math.sin(angle);
		if((90-180*j/rows)%90==0 && (90-180*j/rows)%180!=0)a=(90-180*j/rows)>0?1:-1;
		if((90-180*j/rows)%180==0)a=0;
		var sy =  -r*a;
		vertices.push(i*15,sy);
	}
}

Als nächstes wollen wir sehen, wie die Koordinate von x berechnet wird. Nehmen Sie zunächst die Ebene heraus Abschnitt mit Radius r1, wie unten gezeigt

Verwenden Sie trigonometrische Funktionen, um die x-Koordinate im Diagramm zu berechnen

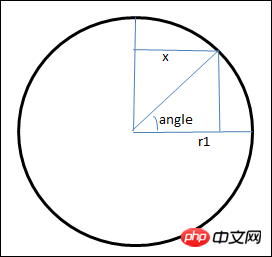Zu diesem Zeitpunkt wenn Sie nur die berechnete

var b = Math.cos(angle*Math.PI/180);
var x =  r1*b;

for(i=0;i<=cols;i++){
	for(j=0;j<=rows;j++){
		var sa = Math.cos(angle);
		if((90-180*j/rows)%180==0)sa=1;
		var sr =  Math.abs(r*sa);
		var angle2 = 360*(i+1)/cols;
		var b = Math.cos(angle2*Math.PI/180);
		if(angle2%360==0)b=1;
		else if(angle2%180==0)b=-1;
		var sx =  sr*b;
		vertices.push(sx,j*15);
	}
}

Der nächste Schritt ist einfach: Ersetzen Sie das leere Bild durch eine Draufsicht der Erde. Der Code lautet wie folgt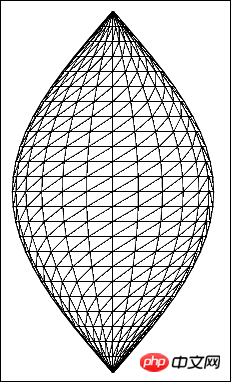

for(i=0;i<=cols;i++){
	for(j=0;j<=rows;j++){
		var angle = (90-180*j/rows)*Math.PI/180;
		var a = Math.sin(angle);
		if((90-180*j/rows)%90==0 && (90-180*j/rows)%180!=0)a=(90-180*j/rows)>0?1:-1;
		if((90-180*j/rows)%180==0)a=0;
		var sy =  -r*a;
		var sa = Math.cos(angle);
		if((90-180*j/rows)%180==0)sa=1;
		var sr =  Math.abs(r*sa);
		var angle2 = 360*(i+1)/cols;
		var b = Math.cos(angle2*Math.PI/180);
		if(angle2%360==0)b=1;
		else if(angle2%180==0)b=-1;
		var sx =  sr*b;
		vertices.push(sx, sy);
	}
}

Als nächstes ist es an der Zeit, die Erde gemäß dem im vorherigen Artikel vorgestellten Inhalt zu drehen Das an die Funktion drawtriangles übergebene uvtData-Array sind die relativen Positionen jedes kleinen Dreiecks im Originalbild. Sie bestimmen die Startposition des Zeichnens des Bildes, wenn eine Reihe von Positionen, z. B. 0123, in 1230 umgewandelt wird In 2301 umgewandelt werden, und die Position wird auf diese Weise kontinuierlich transformiert, dann ist visuell, dass die Drehung tatsächlich erreicht wurde, dann muss im Code nur noch geteilt werden. Das fertige Array wird entsprechend jeder Spalte und jedes Mal, wenn die beiden verschoben werden, verschoben Dreieckssätze in der ersten Spalte werden in die letzte Spalte verschoben, sodass die beiden Dreieckssätze in der zweiten Spalte zur ersten Spalte werden, sodass durch ständige Transformation eine Die Erde dreht sich

earthBitmapData = new LBitmapData(imglist["earth"]);

for (i = 0; i <= rows; i++) {
	uvtData.push(uvtData.shift());
	uvtData.push(uvtData.shift());
}

Auch hier ist für die in diesem Artikel vorgestellten Inhalte die Unterstützung von Version 1.5.1 oder höher der HTML5-Open-Source-Engine lufylegend erforderlich. Die Veröffentlichungsadresse von lufylegend Version 1.5.1 lautet wie folgt

Das Obige ist der Inhalt von HTML5 Advanced Programming Graphic Distortion und seiner Anwendung Drei (Erweiterung). Weitere verwandte Inhalte finden Sie auf der chinesischen PHP-Website (). m.sbmmt.com)!