Minimale Kosten für die Verbindung zweier Punktgruppen

1595. Minimale Kosten für die Verbindung zweier Punktgruppen

Schwierigkeit:Schwer

Themen:Array, dynamische Programmierung, Bitmanipulation, Matrix, Bitmaske

Sie erhalten zwei Gruppen von Punkten, wobei die erste Gruppe die Größe₁Punkte hat, die zweite Gruppe die Größe₂Punkte hat und die Größe₁> = Größe₂.

Die Kosten der Verbindung zwischen zwei beliebigen Punkten werden in einer Größe₁x Größe₂-Matrix angegeben, wobei cost[i][j] die Kosten für die Verbindung von Punkt i sind der ersten Gruppe und Punkt j der zweiten Gruppe. Die Gruppen sind verbunden, wennjeder Punkt in beiden Gruppen mit einem oder mehreren Punkten in der gegenüberliegenden Gruppe verbunden ist. Mit anderen Worten: Jeder Punkt der ersten Gruppe muss mit mindestens einem Punkt der zweiten Gruppe verbunden sein, und jeder Punkt der zweiten Gruppe muss mit mindestens einem Punkt der ersten Gruppe verbunden sein.

Geben Siedie Mindestkosten zurück, die für die Verbindung der beiden Gruppen erforderlich sind.

Beispiel 1:

• Eingabe:Kosten = [[15, 96], [36, 2]]
• Ausgabe:17
• Erklärung:Die optimale Art, die Gruppen zu verbinden, ist:

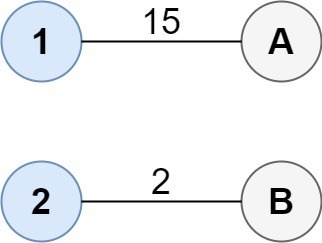
1--A 2--B This results in a total cost of 17.

Beispiel 2:

• Eingabe:Kosten = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
• Ausgabe:4
• Erklärung:Der optimale Weg, die Gruppen zu verbinden, ist:

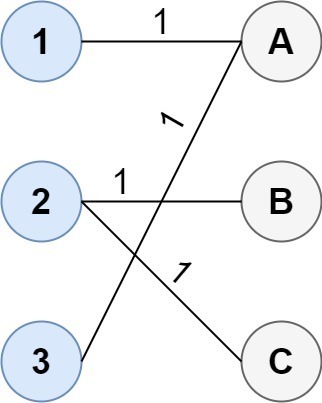
1--A 2--B 2--C 3--A This results in a total cost of 4.

Beachten Sie, dass mehrere Punkte mit Punkt 2 in der ersten Gruppe und Punkt A in der zweiten Gruppe verbunden sind. Dies spielt keine Rolle, da die Anzahl der Punkte, die verbunden werden können, unbegrenzt ist. Wir kümmern uns nur um die minimalen Gesamtkosten.

Beispiel 3:

• Eingabe:Kosten = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8] ]
• Ausgabe:10

Einschränkungen:

• Größe₁== Kosten.Länge
• Größe₂== Kosten[i].Länge
• 1 <= Größe₁, Größe₂<= 12
• Größe₁>= Größe₂
• 0 <= Kosten[i][j] <= 100

Hinweis:

1. Jeder Punkt auf der linken Seite wäre entweder mit genau einem Punkt verbunden, der bereits mit einem linken Knoten verbunden ist, oder mit einer Teilmenge der Knoten auf der rechten Seite, die mit keinem Knoten verbunden sind
2. Verwenden Sie dynamische Programmierung mit Bitmaskierung, wo der Status sein wird (Anzahl der in der ersten Gruppe zugewiesenen Punkte, Bitmaske der in der zweiten Gruppe zugewiesenen Punkte).

Lösung:

Wir können die dynamische Programmierung mit Bitmasking nutzen. Die Idee besteht darin, die Kosten zu minimieren, indem jeder Punkt in der ersten Gruppe berücksichtigt und versucht wird, ihn mit allen Punkten in der zweiten Gruppe zu verbinden.

Dynamischer Programmieransatz (DP) mit Bitmaskierung

Schritte:

1. Staatsvertretung:

   • Verwenden Sie eine DP-Tabelle dp[i][mask], wobei:
     • i ist der Index in der ersten Gruppe (im Bereich von 0 bis size1-1).
     • Maske ist eine Bitmaske, die darstellt, welche Punkte in der zweiten Gruppe verbunden wurden.

2. Zustandsübergang:

   • Versuchen Sie, jeden Punkt in der ersten Gruppe mit jedem Punkt in der zweiten Gruppe zu verbinden, und aktualisieren Sie die DP-Tabelle entsprechend.
   • Wenn ein neuer Punkt in der zweiten Gruppe verbunden wird, aktualisieren Sie das entsprechende Bit in der Maske.

3. Basisfall:

   • Beginnen Sie mit dp[0][0] = 0 (zunächst keine Verbindungen).

4. Ziel:

   • Berechnen Sie die Mindestkosten für dp[size1][(1 << size2) - 1], die die Verbindung aller Punkte aus beiden Gruppen darstellen.

Lassen Sie uns diese Lösung in PHP implementieren:1595. Minimale Kosten für die Verbindung zweier Punktgruppen

        
Erläuterung:
        

         
Das DP-Array dp[i][mask] speichert die Mindestkosten für die Verbindung der ersten i Punkte aus Gruppe 1 mit den Punkten in Gruppe 2, wie durch mask angegeben.
         
Die verschachtelten Schleifen durchlaufen jede Kombination aus i und mask und versuchen, die optimalen Kosten zu finden, indem sie alle möglichen Verbindungen berücksichtigen.
         
Am Ende berechnet die Lösung die Mindestkosten unter Berücksichtigung der Szenarien, in denen einige Punkte in der zweiten Gruppe möglicherweise noch nicht verbunden sind, und stellt sicher, dass alle Punkte verbunden sind.
        
Dieser Ansatz geht effizient mit den Einschränkungen des Problems um und stellt die minimalen Kosten für die Verbindung der beiden Gruppen sicher.
Kontaktlinks
Wenn Sie diese Serie hilfreich fanden, denken Sie bitte darüber nach, demRepositoryeinen Stern auf GitHub zu geben oder den Beitrag in Ihren bevorzugten sozialen Netzwerken zu teilen? Ihre Unterstützung würde mir sehr viel bedeuten!
Wenn Sie weitere hilfreiche Inhalte wie diesen wünschen, folgen Sie mir gerne:
        

         
LinkedIn
         
GitHub
        
Das obige ist der detaillierte Inhalt vonMinimale Kosten für die Verbindung zweier Punktgruppen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!