二叉搜索树是一种数据结构,它允许我们在短时间内保留数字的排序列表。它也被称为二叉树,因为每个树节点只能有两个兄弟节点。二叉搜索树可用于搜索数字是否存在;它被称为搜索树。运行时间复杂度为O(log(n))时间;二叉搜索树与基本二叉树的区别如下 –
开始您的免费软件开发课程
网络开发、编程语言、软件测试及其他
1.左子树的节点都小于根节点。
2.右子树的节点都大于根节点
3.子树的每个节点同样都是 BST,这意味着它们具有与节点本身相同的两个品质。
1.设指定数组为:
给定数组:[8, 6, 2, 7, 9, 12, 4, 10]
2.让我们从顶部元素 43 开始。插入 43 作为树的根。
3.如果下一个元素小于根节点元素,则应将其作为左子树的根插入。
4.如果不是,则应将其插入为右子树的根。
下图描述了使用提供的元素构建二叉搜索树的过程。
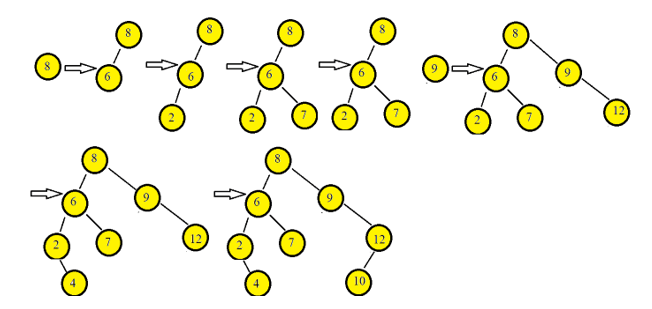
二分搜索树操作:
Java中二叉搜索树支持的操作如下表所示 –
1. BST 搜索 – 在二叉搜索树中,查找某个元素的位置。
2. BST 中的插入 – 在二叉搜索树的适当位置添加新元素可确保二叉搜索树属性不会被破坏。
3. BST 中的删除 – 删除二叉搜索树中的特定节点。但是,根据节点拥有的子节点数量,可能会出现多种删除场景。
Java 中二叉搜索树的示例,对二叉搜索树执行操作 –
//程序可以在Eclipse IDE、JAVA 11中测试
package jex;
import java.util.Scanner;
class binarySearchTree {
//node class that defines BST node
class Node {
int key;
Node left, right;
public Node(int data){
key = data;
left = right = null;
}
}
// binary search tree root node
Node root;
// Constructor for binary search tree, first empty tree
binarySearchTree(){
root = null;
}
//delete a node from binary search tree
void deleteKey(int key) {
root = delete(root, key);
}
//recursive delete function
Node delete(Node root, int key) {
// if tree is empty
if (root == null) return root;
//traverse the tree
if (key < root.key)
//traverse left subtree
root.left = delete(root.left, key);
else if (key > root.key)
//traverse right subtree
root.right = delete(root.right, key);
else {
// if node having only one child
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// if node has two children;
root.key = minKey(root.right);
// removing the inorder sibling
root.right = delete(root.right, root.key);
}
return root;
}
int minKey(Node root) {
// initially min is root
int min = root.key;
// find minimum value
while (root.left != null) {
min = root.left.key;
root = root.left;
}
return min;
}
// insert a node in binary search tree
void insertKey(int key) {
root = insert(root, key);
}
// recursively insert a node
Node insert(Node root, int key) {
// initially, tree is empty
if (root == null) {
root = new Node(key);
return root;
}
// traverse the tree
if (key<root.key)
//insert in the left subtree
root.left = insert(root.left, key);
else if (key > root.key)
//insert in the right subtree
root.right = insert(root.right, key);
// return
return root;
}
// function to travel inorder of binary search tree
void inorder() {
inorder(root);
}
// recursively traverse the binary search tree
void inorder(Node root) {
if (root != null) {
inorder(root.left);
System.out.print(root.key + " ");
inorder(root.right);
}
}
boolean searchKey(int key) {
root = search(root, key);
if (root!= null)
return true;
else
return false;
}
//recursive insert function
Node search(Node root, int key) {
// If root is null or key is present at root
if (root==null || root.key==key)
return root;
// when val is greater than root's key
if (root.key > key)
return search(root.left, key);
// when val is lesser than root's key
return search(root.right, key);
}
}
public class client{
public static void main(String[] args) {
binarySearchTree t = new binarySearchTree();
// inserting 8, 6, 2, 7, 9, 12, 4, 10 data into the binary search tree
t.insertKey(8);
t.insertKey(6);
t.insertKey(2);
t.insertKey(7);
t.insertKey(9);
t.insertKey(12);
t.insertKey(4);
t.insertKey(10);
//print the binary search tree
System.out.println( "The binary search tree created with the input data :");
t.inorder();
//delete the leaf node
System.out.println( "\nThe binary search tree after deleting 4 leaf node :");
t.deleteKey(4);
t.inorder();
//delete the node with one child
System.out.println( "\nThe binary search tree after Delete 12 node with 1 child is :");
t.deleteKey(12);
t.inorder();
//search a key in the binary search tree
boolean res = t.searchKey (9);
System.out.println( "\n The node 9 found in binary search tree is :" + res );
res = t.searchKey (12);
System.out.println( "\n The node 10 found in binary search tree is :" + res );
}
}输出:
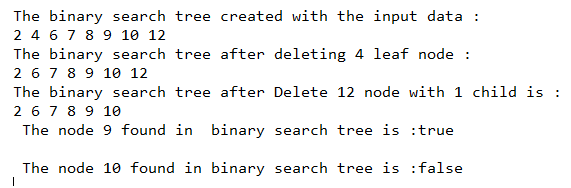
如上面的程序,创建了binarySearchTree类,它包含另一个内部类Node,还包含构造函数和方法。类中定义的方法有deleteKey()、delete()、minKey()、insertKey()、insert()、inorder()、searchKey()和search()来执行具体操作。在 main 函数中,创建了 binarySearchTree 类对象,向其中插入一些元素,然后在其对象上调用二叉搜索树类的方法,如上面的输出所示。
二叉搜索树也称为二叉树,因为每个树节点只能有两个兄弟节点。二叉搜索树是一种数据结构,可以在短时间内保留数字的排序列表。二叉查找树可以进行的操作:遍历、插入、删除、查找。
以上是Java 中的二叉搜索树的详细内容。更多信息请关注PHP中文网其他相关文章!




