本节分析并设计了一种使用动态规划查找斐波那契数的有效算法。第18.3节,案例研究:计算斐波那契数,给出了查找斐波那契数的递归方法,如下:
/**求斐波那契数列的方法*/
公共静态长 fib(长索引){
if (index == 0) // 基本情况
返回 0;
else if (index == 1) // 基本情况
返回 1;
else // 归约和递归调用
返回 fib(索引 - 1) + fib(索引 - 2);
}
我们现在可以证明这个算法的复杂度是O(2^n)。为了方便起见,设索引为n。令 T(n) 表示查找 fib(n) 的算法的复杂度,c 表示将索引与 0 和 1 进行比较的常数时间;也就是说,T(1) 和 T(0) 是 c。因此,

与汉诺塔问题的分析类似,我们可以证明T(n)是O(2^n)。
但是,这个算法效率不高。是否有一种有效的算法来查找斐波那契数?递归 fib 方法的问题在于该方法使用相同的参数进行冗余调用。例如,要计算 fib(4),将调用 fib(3) 和 fib(2)。为了计算 fib(3),需要调用 fib(2) 和 fib(1)。请注意,fib(2) 被冗余调用。我们可以通过避免使用相同参数重复调用 fib 方法来改进它。请注意,新的斐波那契数是通过将序列中的前两个数相加而获得的。如果使用两个变量 f0 和 f1 来存储前面的两个数字,则可以通过添加 f0 立即获得新数字 f2 与 f1。现在,您应该通过将 f1 分配给 f0 并将 f2 分配给 f1 来更新 f0 和 f1 ,如下图。

新方法在下面的代码中实现。
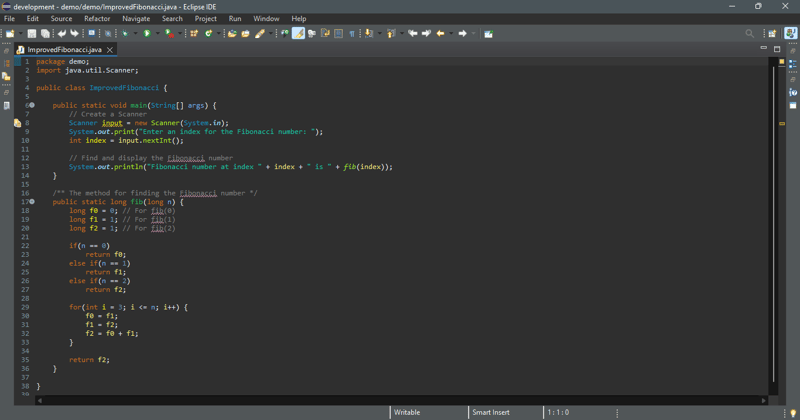
输入斐波那契数列的索引:6
索引 6 处的斐波那契数是 8
输入斐波那契数列的索引:7
索引 7 处的斐波那契数是 13
显然,这个新算法的复杂度是O(n)。这是对递归 O(2^n) 算法的巨大改进。
这里介绍的计算斐波那契数的算法使用了一种称为动态规划的方法。动态规划是解决子问题,然后组合子问题的解以获得总体解决方案的过程。这自然会导致递归解决方案。然而,使用递归效率很低,因为子问题重叠。动态规划背后的关键思想是只解决每个子问题一次,并将子问题的结果存储起来供以后使用,以避免子问题的冗余计算。
以上是使用动态规划查找斐波那契数的详细内容。更多信息请关注PHP中文网其他相关文章!




