一、鍵點法:
確定φ值時,考慮函數y=Asin(ωx φ) B與x軸的交點。我們需要找出最開始與x軸相交的點的橫座標,即設ωx φ=0。這樣就可以確定φ的值。 為了選擇正確的點來代入解析式,我們需要注意點屬於「五點法」中的哪一個點。在“五點法”中,我們選擇的是“第一點”,這是指影像上升時與x軸相交的點。因此,此時ωx φ=0。 請注意,回答的字數不能超過112個。
「最大值點」(即圖象的「峰點」)時
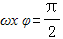
#「最小值點」(即圖象的「谷點」)時
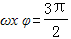
#二、代入法:
可以透過將已知點代入方程式或求解影像與直線交點來確定A、ω和B的值。需注意交點位置。
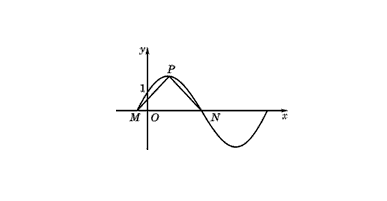
#擴充資料:
三角形函數y=Asin(ωx φ)單調性的方法:
1、我們可以從複合函數的角度去理解函數y=Asin(ωx φ)的單調性。複合函數的單調性由內層函數和外層函數共同決定的。
若在某一區間內內層函數和外層函數的單調性相同,則複合函數為增函數。若在某一區間內內層函數和外層函數的單調性相反,則複合函數為減函數。簡言之,同增異減。
2、函數y=Asin(ωx φ)的圖像是由函數y=sinx經過伸縮平移變換變換得到的。函數y=Asin(ωx φ)的單調性也是依據函數y=sinx解。
函數y=Asin(ωx φ)可以看成是由函數y=sint和函數t=ωx φ複合而成的。函數t=ωx φ是一次函數,它的單調性由ω的正負決定。
所以我們只要把(ωx φ)看成一個整體代入y=sint的單調區間。
例如函數y=sint的單調增區間為[-(π/2) 2kπ,(π/2) 2kπ],則我們可以將t整體替換為ωx φ,即-(π/2) 2kπ≤ ωx φ≤(π/2) 2kπ。
我們只需要解不等式-(π/2) 2kπ≤(ωx φ)≤(π/2) 2kπ就可以得到函數 y=Asin(ωx φ)的單調區間。
3、為了減少分析的難度,我們一般都利用誘導公式把函數y=Asin(ωx φ)中的ω變成正數,這樣我們就能保證一次函數t=ωx φ在實數集上為增函數。
由複合函數的性質知道,我們要函數y=Asin(ωx φ)的單調增(減)區間則將(ωx φ)整體帶入函數y=sint的單調增(減)區間,再結合A的正負,最後解出x的範圍。解出的x範圍就是函數y=Asin(ωx φ)的單調區間。
參考資料來源:百科全書-三角函數
直線的斜率計算公式:k=(y2-y1)/(x2-x1)
由一條直線與右邊X軸所成的角的正切。
k=tanα=(y2-y1)/(x2-x1)或(y1-y2)/(x1-x2)
當直線L的斜率存在時,對於一次函數y=kx b(斜截式),k即該函數影像(直線)的斜率。
擴充資料
當直線L的斜率不存在時,斜截式y=kx b 當k=0時 y=b
當直線L的斜率存在時,點斜式y2—y1=k(X2—X1),
當直線L在兩個座標軸上存在非零截距時,有截距式X/a y/b=1
對於任意函數上任一點,其斜率等於其切線與x軸正方向的夾角,即tanα
斜率計算:ax by c=0中,k=-a/b.
直線斜率公式:k=(y2-y1)/(x2-x1)
兩條垂直相交直線的斜率相乘積為-1:k1*k2=-1.
當k>0時,直線與x軸夾角越大,斜率越大;當k
以上是如何使用三角形函數y=Asin(wx+φ)中的相位角φ的詳細內容。更多資訊請關注PHP中文網其他相關文章!




