一個正方形是一個具有四條邊長度相等的二維形狀。正方形的對邊是平行的,所有四個內角都是直角,對角線長度相等。在本文中,我們將檢查如何確認給定的四個點是否形成一個正方形。
我們將得到一個有四個點的正方形,即A、B、C、D,如圖所示−
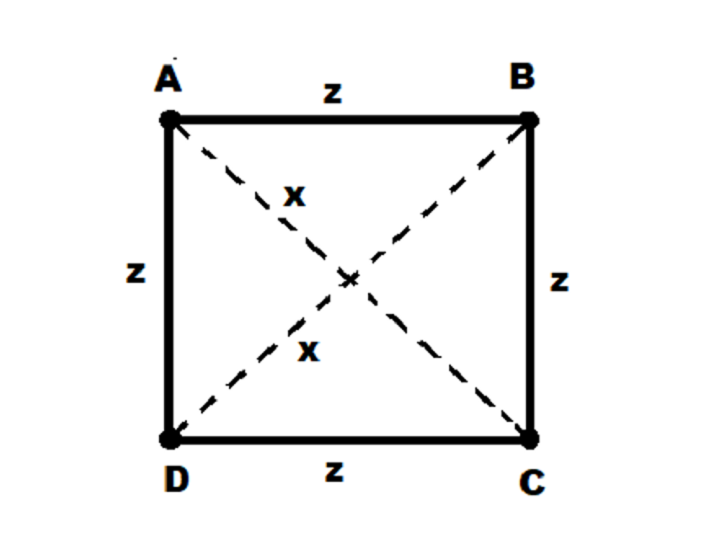
我們需要從這些點來檢查它們是否形成一個正方形。為了檢查這一點,它應滿足以下條件−
點A和點C之間的距離,以及點B和點D之間的距離即「x」應該相等。
點A和點B之間的距離,點B和點C之間的距離,點C和點D之間的距離,點D和點A之間的距離即「z」應該相等。
我們將使用公式找到兩點之間的距離 -
$$\mathrm{d=\sqrt{(x_{2}-x_{1})^2(y_{2}-y_{1})^2}}$$
點1將是(x1,y1),點2將是(x2,y2)。
讓我們開始吧!
給定四個輸入點為 -
P1(3,7), P2(4,3), P3(7,8), P4(1,9)
將其放入距離公式中並檢查是否滿足平方條件,結果將為 -
給定四個點不構成一個正方形。
給定四個輸入點為 -
P1(20,20), P2(20,10), P3(10,10), P4(10,20)
將其放入距離公式中並檢查是否滿足平方條件,結果將為 -
給定四個點形成一個正方形。
步驟-1 − 宣告並初始化變數。
步驟-2 − 求圓的中心1和中心2之間的距離。
第三步 - 檢查五個距離條件。
步驟-4 − 列印結果。
我們以不同的方式提供了解決方案。
透過使用靜態輸入
#透過使用使用者定義的方法
讓我們逐一查看程式及其輸出。
在這種方法中,將分配點值。然後根據演算法,我們將找出給定的四個點是否形成一個正方形。
public class Main{
//main method
public static void main(String[] args){
//declaring variables
int x1=3, x2=4, x3=7, x4=1;
int y1=7, y2=3, y3=8, y4=9;
double d1, d2, d3, d4, d5, d6;
//applyinng logic
d1 = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1);
d2 = (x3 - x2) * (x3 - x2) + (y3 - y2) * (y3 - y2);
d3 = (x4 - x3) * (x4 - x3) + (y4 - y3) * (y4 - y3);
d4 = (x1 - x4) * (x1 - x4) + (y1 - y4) * (y1 - y4);
d5 = (x4 - x2) * (x4 - x2) + (y4 - y2) * (y4 - y2);
d6 = (x3 - x1) * (x3 - x1) + (y3 - y1) * (y3 - y1);
if (d1 == 0 || d2 == 0 || d3 == 0 || d4 == 0 || d5 == 0 || d6 == 0){
System.out.println("Given four points do not form a square");
}
else if (d1 == d2 && d2 == d3 && d3 == d4 && d5 == d6){
//prints if four points form square
System.out.println("Given four points form a square");
} else {
//prints if four points do not form square
System.out.println("Given four points do not form a square");
}
}
}
Given four points do not form a square
在這種方法中,將分配點值。然後透過傳遞給定的值來呼叫一個使用者定義的方法,並根據演算法判斷給定的四個點是否形成一個正方形。
public class Main{
//main method
public static void main(String[] args){
//creating objects of Point
Point p1 = new Point(20, 20);
Point p2 = new Point( 20, 10 );
Point p3 = new Point(10, 10 );
Point p4 = new Point( 10, 20 );
//calling user defined method
if(isSquare(p1, p2, p3, p4)==true){
//print if four points form a square
System.out.println("Given four points form a square");
}
else{
//print if points does not form a square
System.out.println("Given four points do not form a square");
}
}
// Declaring Point class
static class Point{
int x, y;
public Point(int x, int y){
this.x = x;
this.y = y;
}
};
//function to find square of distance from point 'p' to point 'q'
static int distSq(Point p, Point q){
return (p.x - q.x) * (p.x - q.x) + (p.y - q.y) * (p.y - q.y);
}
//user defined method
static boolean isSquare(Point p1, Point p2, Point p3, Point p4){
int d1 = distSq(p1, p2);
int d2 = distSq(p2, p3);
int d3 = distSq(p3, p4);
int d4 = distSq(p4, p1);
int d5 = distSq(p1, p3);
int d6 = distSq(p2, p4);
if (d1 == 0 || d2 == 0 || d3 == 0 || d4 == 0 || d5 == 0 || d6 == 0)
return false;
if (d1 == d2 && d2 == d3 && d3 == d4 && d5 == d6){
//it returns true if (p1, p2, p3, p4) form a square
return true;
}
//it returns false if (p1, p2, p3, p4) do not form a square
return false;
}
}
Given four points form a square
在這篇文章中,我們使用Java程式語言探討了不同的方法來檢查一條線是否觸碰、相交或位於圓外。
以上是如何在Java中確認給定的四個點是否形成一個正方形?的詳細內容。更多資訊請關注PHP中文網其他相關文章!
