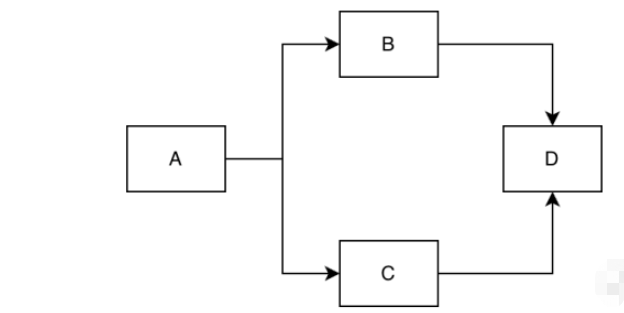
我們本節將介紹與有向圖相關的演算法,因此先對有向圖的一些概念進行解釋;之後的文章將不再對這些概念做具體解釋。首先有向圖節點與節點之間是用帶箭頭的線連接起來的。節點的出度和入度可用來描述,當一條連線的尾部指向該節點時,其出度會增加1;而當一條連線的箭頭指向該節點時,其入度會增加1。看下面這個例子,A的入度為0,出度為2,B的入度為1,出度為1,C的入度為1,出度為1,D的入度為2,出度為0。
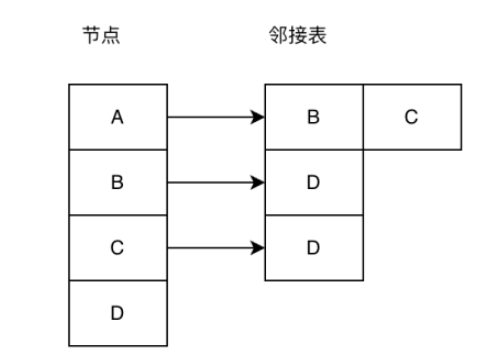
鄰接表:鄰接表是儲存圖結構的一種有效方式,如下圖所示,左邊節點數組儲存圖中所有節點,右側鄰接表儲存節點的相鄰節點。
這篇文章我們要講的是拓樸排序,這是一個針對有向無環圖的演算法,主要是為了解決前驅後繼的關係,也就是我們在完成當前事項的時候需要先完成什麼事項,其實這在我們流程控制裡面用的挺多的。看下面這個圖,我們需要先完成A事項,然後才能去完成B,C事項,B,C事項的屬於並列的,沒有先後順序,但是對於D事項需要在B,C事項完成之後才能進行。而拓樸排序能夠幫助我們找到這個完成事項的合理順序,同時我們看上面這個例子,A事項完成之後,B,C事項是沒有先後順序的,不管是先完成B還是C都符合條件,所以拓樸排序的順序序列不是完全一定的。
首先拓撲排序對應操作的是一個有向無環圖。無環圖,則肯定存在至少一個結點入度為0。在目前情況下,我們需要尋找入度為0的節點進行操作,入度為0,表示目前節點沒有前驅節點,或是前驅節點已經處理,可以直接操作。操作完畢之後,將目前節點的後繼節點入度全部減1,再次查找入度節點為0的節點進行操作,此後就是一個遞歸過程,不斷處理當前情況下入度為0的節點,直至所有節點處理完畢。
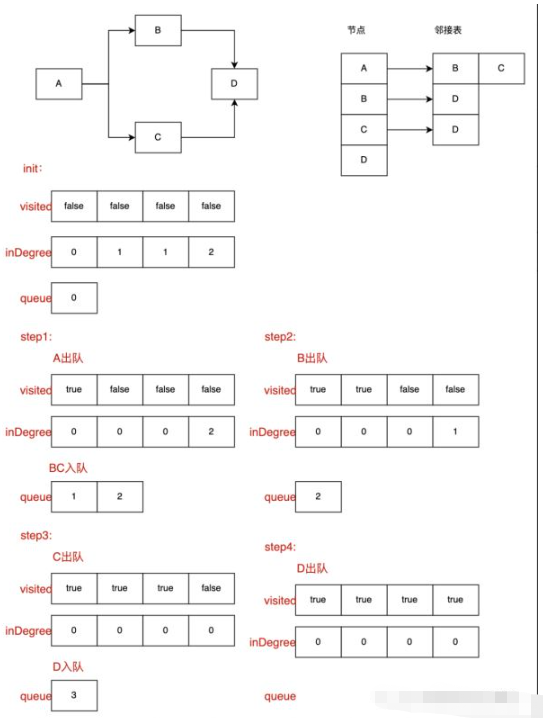
以下是有向圖的結構,其中node儲存著目前圖中的所有節點,adj則儲存對應下標節點的鄰接點。初始化圖時,需指定節點數量、建立節點數組和鄰接數組。提供一個名為addEdge的方法,用於將兩個節點之間建立一條邊,即將後繼節點新增至前驅節點的鄰接表。
public static class Graph{
/**
* 节点个数
*/
private Integer nodeSize;
/**
* 节点
*/
private char[] node;
/**
* 邻接表
*/
private LinkedList[] adj;
public Graph(char[] node) {
this.nodeSize = node.length;
this.node = node;
this.adj = new LinkedList[nodeSize];
for (int i = 0 ; i < adj.length ; i++) {
adj[i] = new LinkedList();
}
}
/**
* 在节点之间加边,前驱节点指向后继节点
* @param front 前驱节点所在下标
* @param end 后继节点所在下标
*/
public void addEdge(int front, int end) {
adj[front].add(end);
}
}拓撲排序首先初始化了兩個臨時數組,一個隊列,一個inDegree數組存儲對應下標節點的入度,因為每次訪問的節點需要前驅節點已經完成,即入度為0,有了這個數組我們就可以比較快速的找到這些節點;另一個是visited數組,標誌當前節點是否已經訪問過,防止多次訪問;一個nodes隊列則保存在目前情況下所有入度為0的節點。 (注意,為了存取方便,我們都是儲存的節點下標step1:初始化inDegree數組,visited數組; step2:遍歷inDegree數組,將所有入度為0的節點入nodes隊列; step3:依序將節點node出隊; 根據visited判斷當前node是否已經被訪問,是,返回step3,否,進行下一步; 將當前節點的鄰接節點入度-1,判斷鄰接節點入度是否為0,為0直接放入nodes隊列,不為0返回step3;
/**
* @param graph 有向无环图
* @return 拓扑排序结果
*/
public List<Character> toPoLogicalSort(Graph graph) {
//用一个数组标志所有节点入度
int[] inDegree = new int[graph.nodeSize];
for (LinkedList list : graph.adj) {
for (Object index : list) {
++ inDegree[(int)index];
}
}
//用一个数组标志所有节点是否已经被访问
boolean[] visited = new boolean[graph.nodeSize];
//开始进行遍历
Deque<Integer> nodes = new LinkedList<>();
//将入度为0节点入队
for (int i = 0 ; i < graph.nodeSize; i++) {
if (inDegree[i] == 0) {
nodes.offer(i);
}
}
List<Character> result = new ArrayList<>();
//将入度为0节点一次出队处理
while (!nodes.isEmpty()) {
int node = nodes.poll();
if (visited[node]) {
continue;
}
visited[node] = true;
result.add(graph.node[node]);
//将当前node的邻接节点入度-1;
for (Object list : graph.adj[node]) {
-- inDegree[(int)list];
if (inDegree[(int)list] == 0) {
//前驱节点全部访问完毕,入度为0
nodes.offer((int) list);
}
}
}
return result;
}public static void main(String[] args) {
ToPoLogicalSort toPoLogicalSort = new ToPoLogicalSort();
//初始化一个图
Graph graph = new Graph(new char[]{'A', 'B', 'C', 'D'});
graph.addEdge(0, 1);
graph.addEdge(0,2);
graph.addEdge(1,3);
graph.addEdge(2,3);
List<Character> result = toPoLogicalSort.toPoLogicalSort(graph);
}執行結果
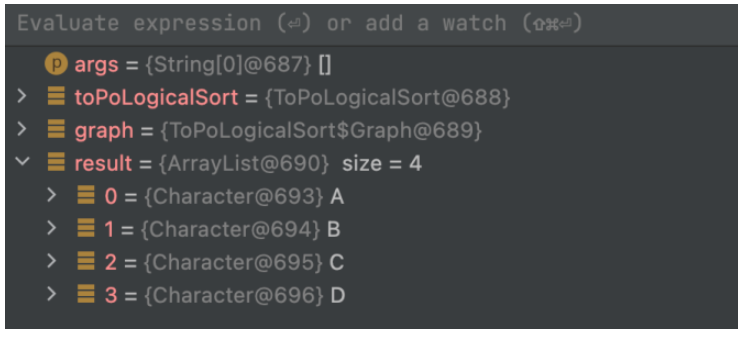
public static void main(String[] args) {
ToPoLogicalSort toPoLogicalSort = new ToPoLogicalSort();
//初始化一个图
Graph graph = new Graph(new char[]{'A', 'B', 'C', 'D','E','F','G','H'});
graph.addEdge(0, 1);
graph.addEdge(0,2);
graph.addEdge(0,3);
graph.addEdge(1,4);
graph.addEdge(2,4);
graph.addEdge(3,4);
graph.addEdge(4,7);
graph.addEdge(4,6);
graph.addEdge(7,5);
graph.addEdge(6,7);
List<Character> result = toPoLogicalSort.toPoLogicalSort(graph);
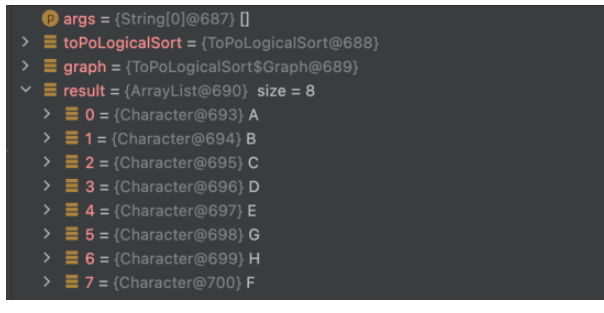
}執行結果
 #
#
以上是Java如何實作拓樸排序的詳細內容。更多資訊請關注PHP中文網其他相關文章!




