計算的複雜度是一個特定演算法在執行時所消耗的計算資源(時間和空間)的量測。
計算複雜度又分為兩類:
1、時間複雜度
時間複雜度不是測量一個演算法或一段程式碼在某個機器或條件下運行所花費的時間。時間複雜度一般指時間複雜性,時間複雜度是一個函數,它定性描述演算法的運行時間,允許我們在不運行它們的情況下比較不同的演算法。例如,帶有O(n)的演算法總是比O(n²)表現得更好,因為它的成長率小於O(n²)。
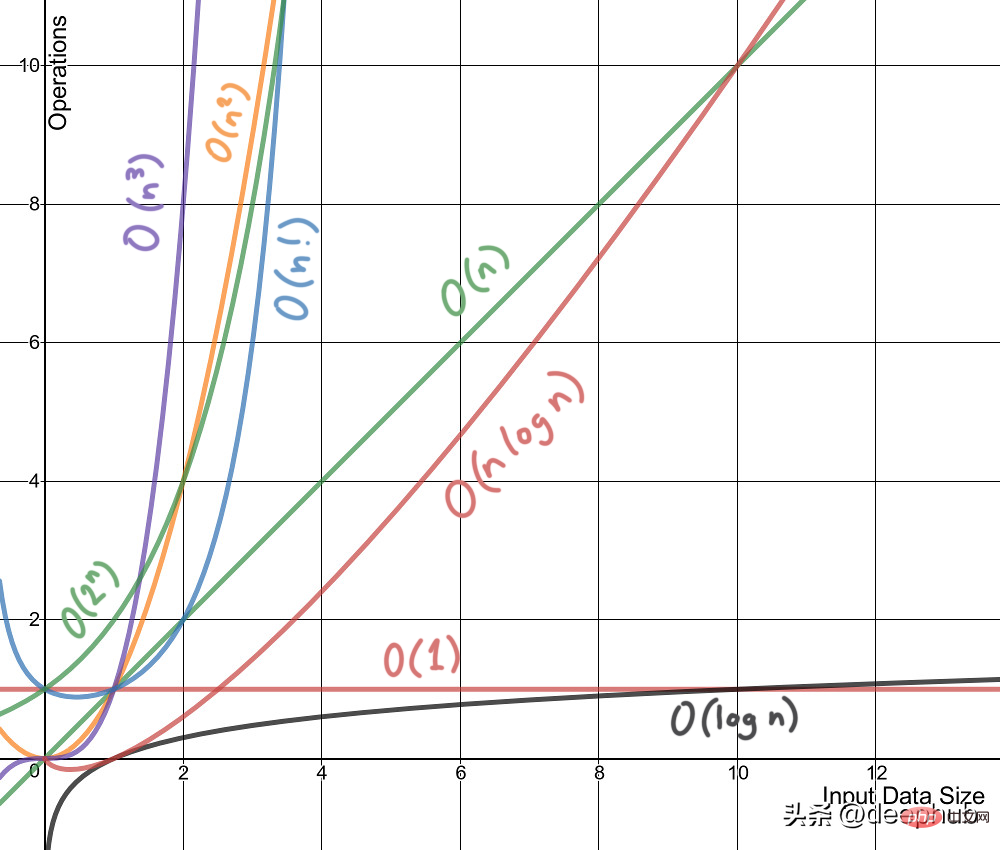
2、空間複雜度
就像時間複雜度是個函數一樣,空間複雜度也是。從概念上講,它與時間複雜度相同,只需將時間替換為空間。維基百科將空間複雜度定義為:
演算法或電腦程式的空間複雜度是解決運算問題實例所需的儲存空間量,以特徵數量作為輸入的函數。
下面我們整理了一些常見的機器學習演算法的計算複雜度。
1、線性迴歸
- n= 訓練樣本數,f = 特徵數
- 訓練時間複雜度:O(f²n f³)
- 預測時間複雜度:O(f)
- 執行階段空間複雜度:O(f)
#2、邏輯迴歸:
- n = 訓練樣本數,f = 特徵數
- 訓練時間複雜度:O(f*n)
- 預測時間複雜度:O(f)
- 運行時空間複雜度:O(f)
3、支援向量機:
- n= 訓練樣本數,f = 特徵數,s= 支援向量的數量
- 訓練時間複雜度:O(n²) 到O(n³),訓練時間複雜度因內核不同而不同。
- 預測時間複雜度:O(f) 到O(s*f):線性核是O(f),RBF 和多項式是O(s*f)
- 運行時空間複雜度:O(s)
4、樸素貝葉斯:
- n= 訓練樣本數,f = 特徵數,c = 分類的類別數
- 訓練時間複雜度:O(n*f*c)
- 預測時間複雜度:O(c*f)
- #運行時空間複雜度:O(c *f)
5、決策樹:
- n= 訓練樣本數,f = 特徵數,d = 樹的深度,p = 節點數
- 訓練時間複雜度:O(n*log(n)*f)
- 預測時間複雜度:O(d)
- 執行階段空間複雜度:O(p)
6、隨機森林:
- n= 訓練樣本數,f = 特徵數,k = 樹的數量,p=樹中的節點數,d =樹的深度
- 訓練時間複雜度:O(n*log(n)*f*k)
- 預測時間複雜度:O(d*k)
- #運行時空間複雜度:O(p*k)
7、K近鄰:
n= 訓練樣本數,f = 特徵數,k= 近鄰數
Brute:
- 訓練時間複雜度:O(1)
- 預測時間複雜度:O(n*f k*f)
- #運行時空間複雜度:O(n*f)
kd-tree:
- 訓練時間複雜度:O(f*n*log(n))
- 預測時間複雜度:O(k*log(n))
- 運行時空間複雜度:O(n*f)
8、K-means聚類:
- n= 訓練樣本數,f = 特徵數,k= 簇數,i = 迭代次數
- 訓練時間複雜度:O(n*f*k *i)
- 運行時空間複雜度:O(n*f k*f)
#
以上是八個常見的機器學習演算法的計算複雜度總結的詳細內容。更多資訊請關注PHP中文網其他相關文章!





