自動證明數學定理是人工智慧的一個初衷,也是一直以來的難題。 到目前為止,人類數學家使用了兩種不同的方式來書寫數學。
第一種是大家都熟悉的方式,也就是用自然語言來描述數學證明。大部分的數學都是以這種方式書寫的,這包括數學課本,數學論文,等等。
第二種稱為形式化數學(formal mathematics)。這是近半個世紀電腦科學家創造的,用來檢驗數學證明的一種工具。
如今看來,電腦可以被用來驗證數學證明,但它們只有在使用專門設計的證明語言時才能做到這一點,而無法處理數學符號和數學家使用的書寫文字的混合。如果把用自然語言寫的數學問題轉換成形式化程式碼,讓電腦更容易解決它們,或許能夠幫助建構能探索數學新發現的機器。這個過程稱為形式化(formalisation),自動形式化(autoformalization)指的是自動從自然語言數學翻譯成形式化語言的任務。
形式化證明的自動化是一項具有挑戰性的任務,深度學習方法在該領域尚未大獲成功,這主要是因為形式化資料的稀缺。事實上,形式化證明本身是非常困難的,而且只有少數專家能做到,這使得大規模的註釋工作並不現實。最大的形式化證明語料庫是用 Isabelle 程式碼 (Paulson, 1994) 編寫的,大小不到 0.6GB,比視覺或自然語言處理中常用的資料集小幾個數量級。為了解決形式證明的稀缺性,過去的研究提出使用合成資料、自我監督或強化學習來合成額外的形式化訓練資料。雖然這些方法在一定程度上緩解了數據的不足,但都無法將大量人工撰寫的數學證明充分利用起來。
我們以語言模型 Minerva為例。當在足夠的資料訓練之後,我們發現它的數學能力非常強,可以在高中數學測驗中拿到高於平均分數。然而這樣的語言模型也有不足,它只能模仿,而無法自主訓練而提升數學程度。形式化證明系統提供了一個訓練環境,但形式化數學的資料非常少。
與形式化的數學不同,非形式化的數學資料是豐富且廣泛可用的。最近,在非形式化數學資料上訓練的大型語言模型展示了令人印象深刻的定量推理能力。然而,它們經常產生錯誤的證明,而自動檢測這些證明中的錯誤推理是很有挑戰性的。
在最近的一項工作中,Google的吳宇懷(Yuhuai Tony Wu)等研究者設計了一種叫做DSP(Draft, Sketch, and Prove )的新方法,將非形式化的數學證明轉化為形式化的證明,從而同時具備形式化系統提供的邏輯嚴謹性和大量的非形式化數據。

論文連結:https://arxiv.org/pdf/2210.12283.pdf
#今年早些時候,吳宇懷與幾位合作者使用了OpenAI Codex 的神經網路進行自動形式化工作,證明了用大型語言模型將非形式化語句自動翻譯成形式化語句的可行性。 DSP 則更進一步,利用大型語言模型從非形式化證明中產生形式化證明草圖。證明草圖由高層次的推理步驟組成,可以由互動式定理證明器這樣的形式化系統來解釋。它們與完整的形式化證明不同,因為它們包含無理由的中間猜想的序列。在 DSP 的最後一步,形式化證明草圖被闡述為一個完整的形式化證明,使用一個自動驗證器來證明所有中間猜想。
吳宇懷表示:現在,我們展示了 LLM 可以將其產生的非形式化證明轉化為經過驗證的形式化證明!
方法部分描述了用於形式化證明自動化的DSP方法,該方法利用非形式化證明來指導自動形式化定理證明器的證明草圖。這裡假設每個問題都有一個非形式化命題和一個描述該問題的形式化命題。整體 pipeline 包括三個階段(如圖 1 所示)。
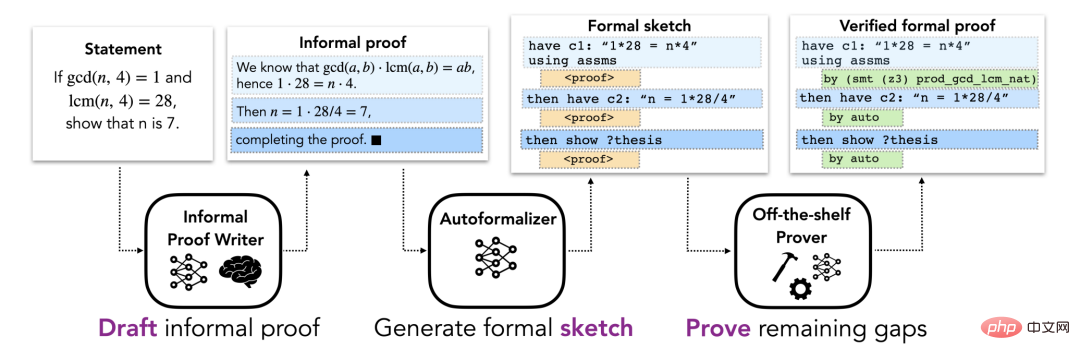
#圖1.
DSP 方法的初始階段,包括根據問題的自然數學語言描述(可能用LATEX)為其尋找非形式化證明。由此產生的非形式化證明被視為後續階段的草稿。在數學教科書中,一般都會提供定理的證明,但有時會缺失或不完整。因此,研究者考慮了與非形式化證明的存在或不存在相對應的兩種情況。
在第一種情況下,研究者假設有一個「真實的」非形式化證明(即由人寫的證明),這是現有數學理論形式化實踐中的典型情況。在第二種情況下,研究者做了一個更普遍的假設,即沒有給出真實的非形式化證明,並且用一個經過非形式化數學資料訓練的大型語言模型來起草證明候選。此語言模型消除了對人類證明的依賴,並能為每個問題產生多種替代解決方案。雖然沒有簡單的方法來自動驗證這些證明的正確性,但非形式化證明只需要在下一階段對產生一個好的形式化證明草圖有用。
形式化證明草圖對解決方案的結構進行編碼,並撇開低層次的細節。直觀地說,它是一個部分證明,概述了高層次的猜想命題。圖 2 是一個證明草圖的具體例子。儘管非形式化證明經常撇開低層次的細節,這些細節不能在形式化證明中排出,這使得非形式化證明到形式化證明的直接轉換變得困難。相反,本文建議將非形式化證明映射到共享相同高層結構的形式化證明草圖上。證明草圖中缺少的低層次細節可以由自動證明器來填補。由於大型非形式化 - 形式化平行語料庫不存在,標準的機器翻譯方法不適合這項任務。相反,這裡使用一個大型語言模型的小樣本學習能力。具體來說,用了一些包含非形式化證明及其相應的形式化草圖的例子對來prompt 該模型,然後是一個有待轉換的非形式化證明,然後讓模型生成後續的token,以獲得所需的形式化草圖。這個模型稱為「自動形式化器」。

############# 證明草圖中的公開猜想#########作為這個過程的最後一部分,研究者執行現成的自動證明器來填補證明草圖中缺失的細節,這裡的「自動證明器」是指能夠產生形式上可驗證的證明的系統。這個框架對自動證明器的具體選擇是不可知的:它可以是符號證明器(如啟發式證明自動化工具)、基於神經網路的證明器或混合方法。如果自動證明器成功地填補了證明草圖中的所有空白,它就會返回最終的形式化證明,可以對照問題的規格進行檢查。如果自動證明器失敗(例如,它超過了分配的時間限制),則認為評估是不成功的。 ######
研究者進行了一系列實驗,包括從 miniF2F 資料集中產生問題的形式化證明,並表明很大一部分定理可以用這種方法自動證明。這裡研究了兩種環境,其中非形式化證明是由人類寫的,或者是由一個在數學文本上訓練的大型語言模型起草的。這兩種設定對應於現有理論形式化過程中經常出現的情況,即通常有非形式化證明,但有時作為練習留給讀者,或者由於空白處的限製而缺失。
表 1 展示了在 miniF2F 資料集上發現的成功形式化證明的比例。結果包括本文實驗的四條 baseline,以及帶有人類編寫的證明和模型生成的證明的 DSP 方法。
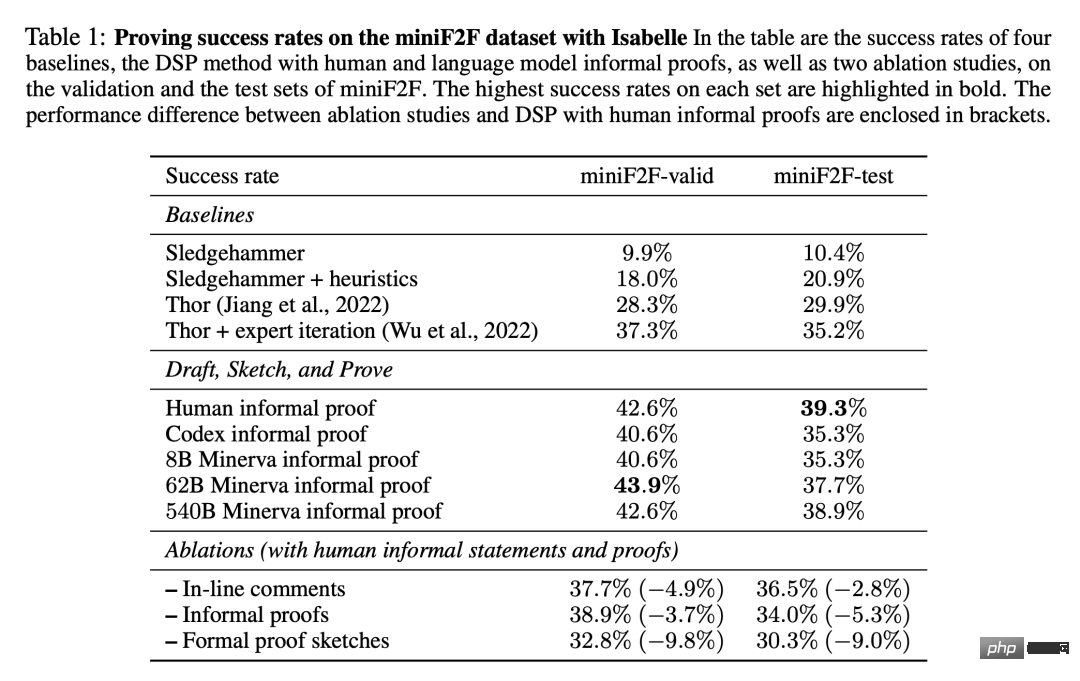
可以看出,附加了11 種啟發式策略的自動證明器大大增加了Sledgehammer 的效能,在miniF2F 的驗證集上將其成功率從9.9% 提高到18.0%,在測試集上從10.4% 提高到20.9%。兩個使用語言模型和證明搜尋的 baseline 在 miniF2F 的測試集上分別達到 29.9% 和 35.2% 的成功率。
基於人類編寫的非形式化證明,DSP 方法在 miniF2F 的驗證和測試集上取得了 42.6% 和 39.3% 的成功率。 488 個問題中共有 200 個可以用這種方式證明。 Codex 模型和 Minerva(8B)模型在解決 miniF2F 上的問題時給出了非常相似的結果:它們都指導自動驗證器分別解決了驗證集和測試集上 40.6% 和 35.3% 的問題。
當切換到 Minerva(62B)模型時,成功率分別上升到 43.9% 和 37.7%。與人所寫的非形式化證明相比,其在驗證集上的成功率高出 1.3%,在測試集上低 1.6%。總的來說,Minerva(62B)模型能夠解決 miniF2F 上的 199 個問題,比用人寫的證明少一個。 Minerva(540B)模型在 miniF2F 的驗證集和測試集中分別解決了 42.6% 和 38.9% 的問題,也產生了 199 個成功的證明。
在兩種情況下,DSP 方法都能有效地引導自動證明器:使用人類的非形式化證明或語言模型產生的非形式化證明。 DSP 幾乎將證明器的成功率提高了一倍,並在使用 Isabelle 的 miniF2F 上產生了 SOTA 性能。此外,更大的 Minerva 模型在指導自動形式化證明器方面幾乎和人類一樣有幫助。
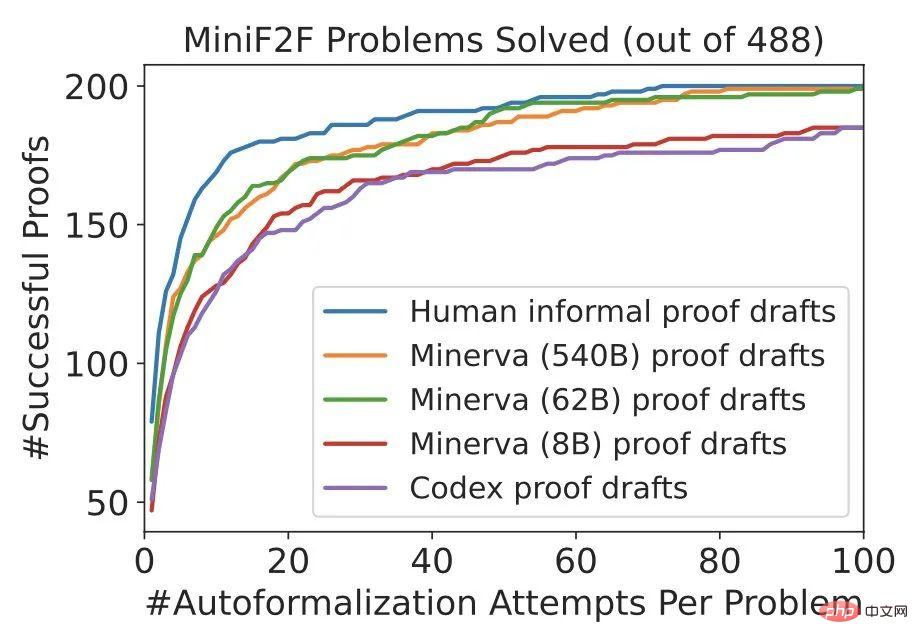
如下圖所示,DSP 方法顯著提高了 Sledgehammer 啟發式證明器的效能(~20% -> ~40%),在 miniF2F 上實現了新的 SOTA。
Minerva 的 62B 和 540B 版本產生的證明與人類的證明非常相似。
更多內容,請參考原文。
以上是AI再捲數學界,DSP新方法將機器證明成功率提高一倍的詳細內容。更多資訊請關注PHP中文網其他相關文章!




