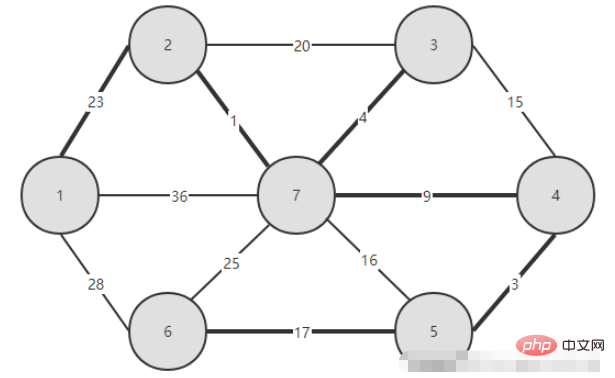
建構最小生成樹還有一個演算法,即Kruskal 演算法:設圖G=(V,E)是無向連通帶權圖,V={1,2,... n};設最小生成樹T=(V,TE),該樹的初始狀態只有n 個節點而無邊的非連通圖T=(V,{}),Kruskal 演算法將這n 個節點看成n 個孤立的連通分支。它首先將所有邊都按權值從小到大排序,然後值要在T 中選的邊數不到n-1,就做這樣貪心選擇:在邊集E 中選擇權值最小的邊(i,j ),如果將邊(i,j)加入集合TE 中不產生迴路,則將邊(i,j)加入邊集TE 中,即用邊(i,j)將這兩個分支合併成一個連通分支;否則繼續選擇下一條最短邊。把邊(i,j)從集合 E 中刪去,繼續上面的貪心選擇,直到 T 中的所有節點都在同一個連通分支上為止。此時,選取的 n-1 條邊恰好構成圖 G 的一棵最小生成樹 T。
Kruskal 演算法用一種很聰明的方法,就是運用集合避圈;如果所選加入邊的起點和終點都在T 集合中,就可以斷定會形成迴路,變的兩個節點不能屬於同一個集合。
演算法步驟
1 初始化。將所有邊都依權值從小到大排序,將每個節點集合號碼初始化為自身編號。
2 依照排序後的順序選擇權值最小的邊(u,v)。
3 如果節點 u 和 v 屬於兩個不同的連通分支,則將邊(u,v)加入邊集 TE 中,並將兩個連通分支合併。
4 若選取的邊數小於 n-1,則轉向步驟2,否則演算法結束。
package graph.kruskal;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;
public class Kruskal {
static final int N = 100;
static int fa[] = new int[N];
static int n;
static int m;
static Edge e[] = new Edge[N * N];
static List<Edge> edgeList = new ArrayList();
static {
for (int i = 0; i < e.length; i++) {
e[i] = new Edge();
}
}
// 初始化集合号为自身
static void Init(int n) {
for (int i = 1; i <= n; i++)
fa[i] = i;
}
// 合并
static int Merge(int a, int b) {
int p = fa[a];
int q = fa[b];
if (p == q) return 0;
for (int i = 1; i <= n; i++) { // 检查所有结点,把集合号是 q 的改为 p
if (fa[i] == q)
fa[i] = p; // a 的集合号赋值给 b 集合号
}
return 1;
}
// 求最小生成树
static int Kruskal(int n) {
int ans = 0;
Collections.sort(edgeList);
for (int i = 0; i < m; i++)
if (Merge(edgeList.get(i).u, edgeList.get(i).v) == 1) {
ans += edgeList.get(i).w;
n--;
if (n == 1)//n-1次合并算法结束
return ans;
}
return 0;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
Init(n);
for (int i = 1; i <= m; i++) {
e[i].u = scanner.nextInt();
e[i].v = scanner.nextInt();
e[i].w = scanner.nextInt();
edgeList.add(e[i]);
}
System.out.println("最小的花费是:" + Kruskal(n));
}
}
class Edge implements Comparable {
int u;
int w;
int v;
@Override
public int compareTo(Object o) {
if (this.w > ((Edge) o).w) {
return 1;
} else if (this.w == ((Edge) o).w) {
return 0;
} else {
return -1;
}
}
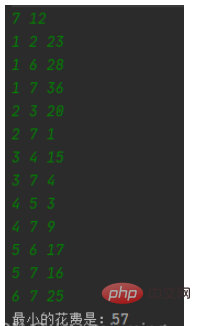
}綠色為輸入,白色為輸出。
以上是Java如何實作Kruskal演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章!




