二元搜尋樹又稱二元排序樹,它或是一棵空樹,或是具有以下性質的二元樹:
1、若它的左子樹不為空,則左子樹上所有節點的值都小於根結點的值。
2、若它的右子樹不為空,則右子樹上所有節點的值都大於根結點的值。
3、它的左右子樹也分別為二元搜尋樹
假設我們已經建構好了一個這樣的二元樹,如下圖
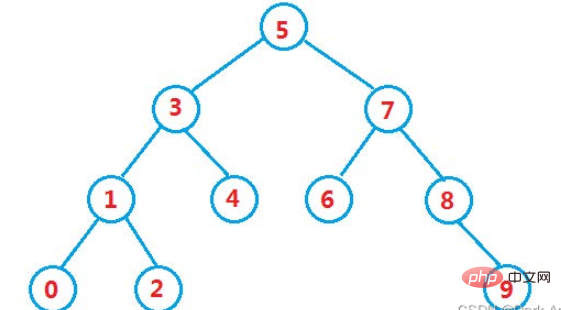
我們要思考的第一個問題是如何找出某個值是否在該二元樹中?
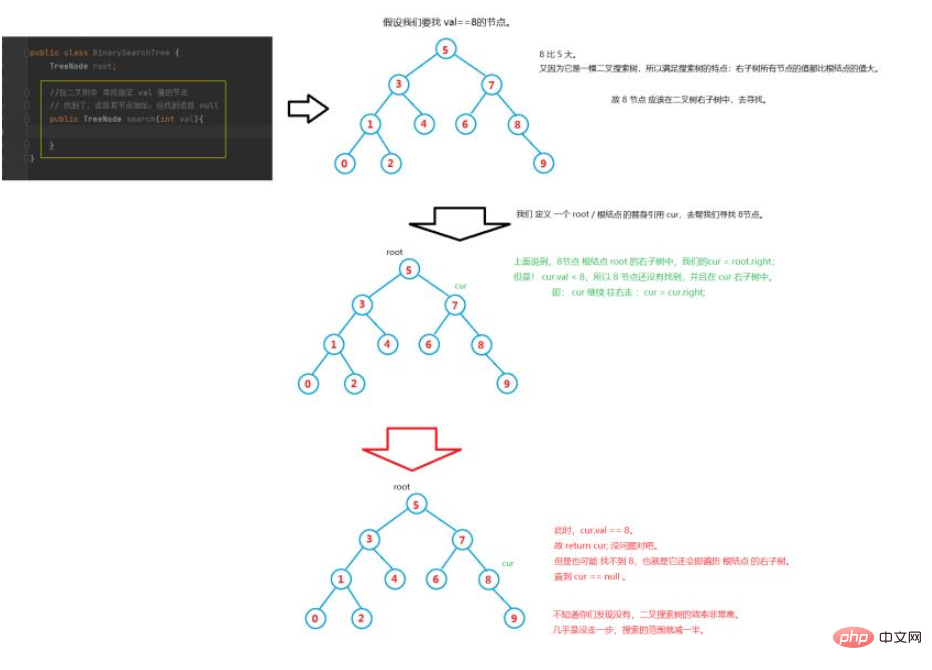
#根據上述的邏輯,我們來把搜尋的方法進行完善。
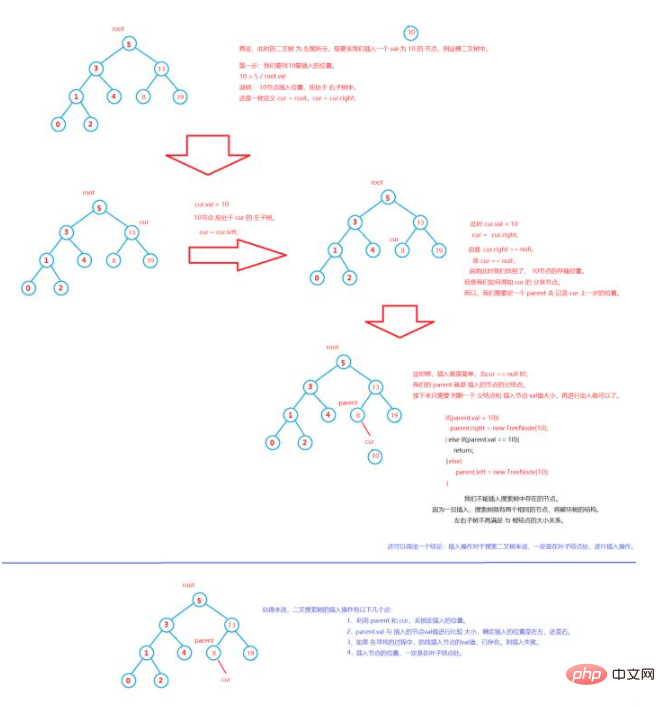
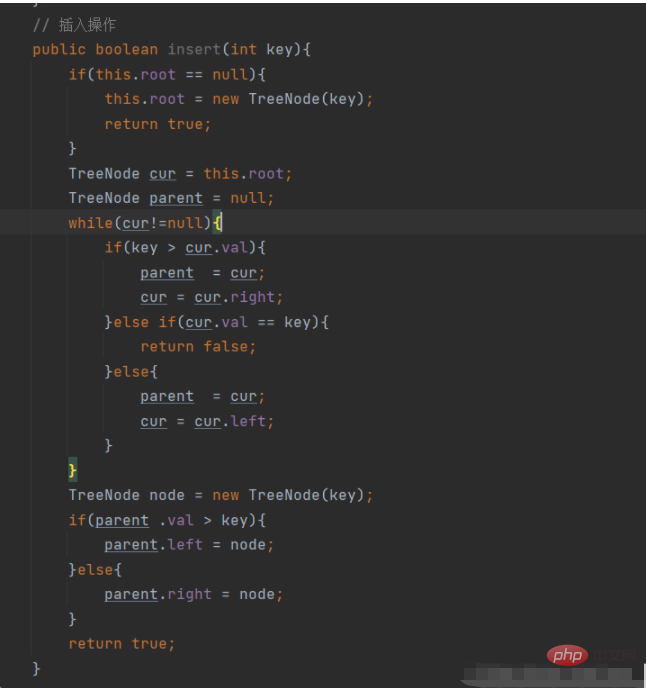
#根據上述邏輯,我們來寫一個插入節點的程式碼。
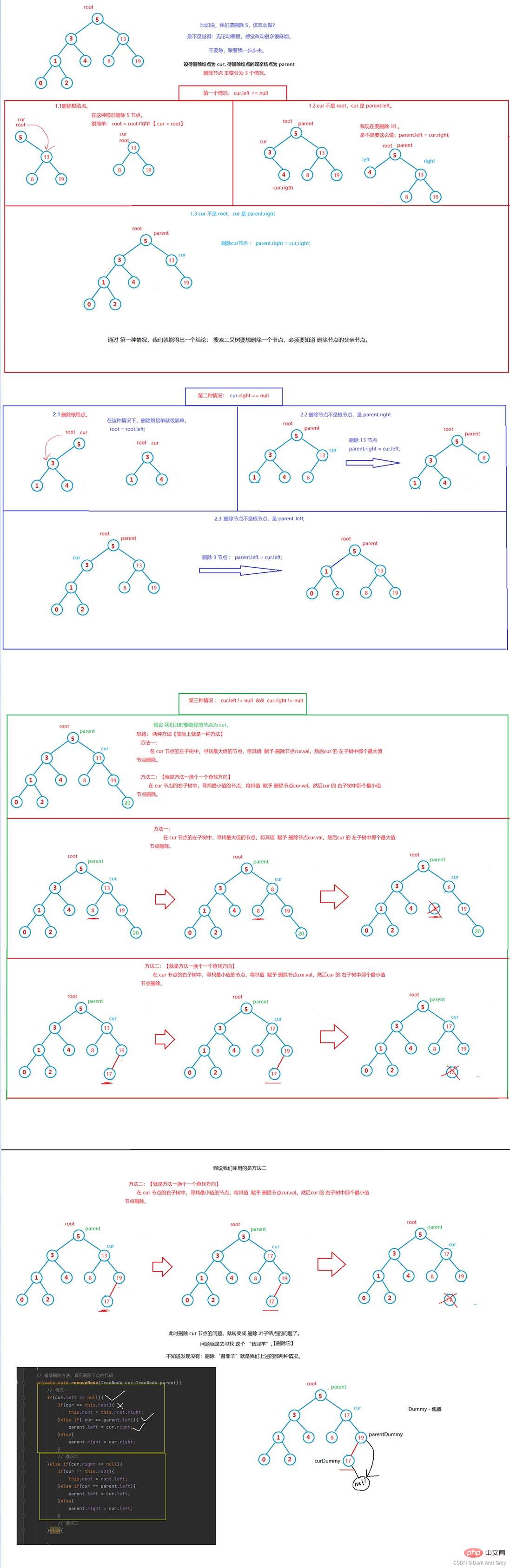
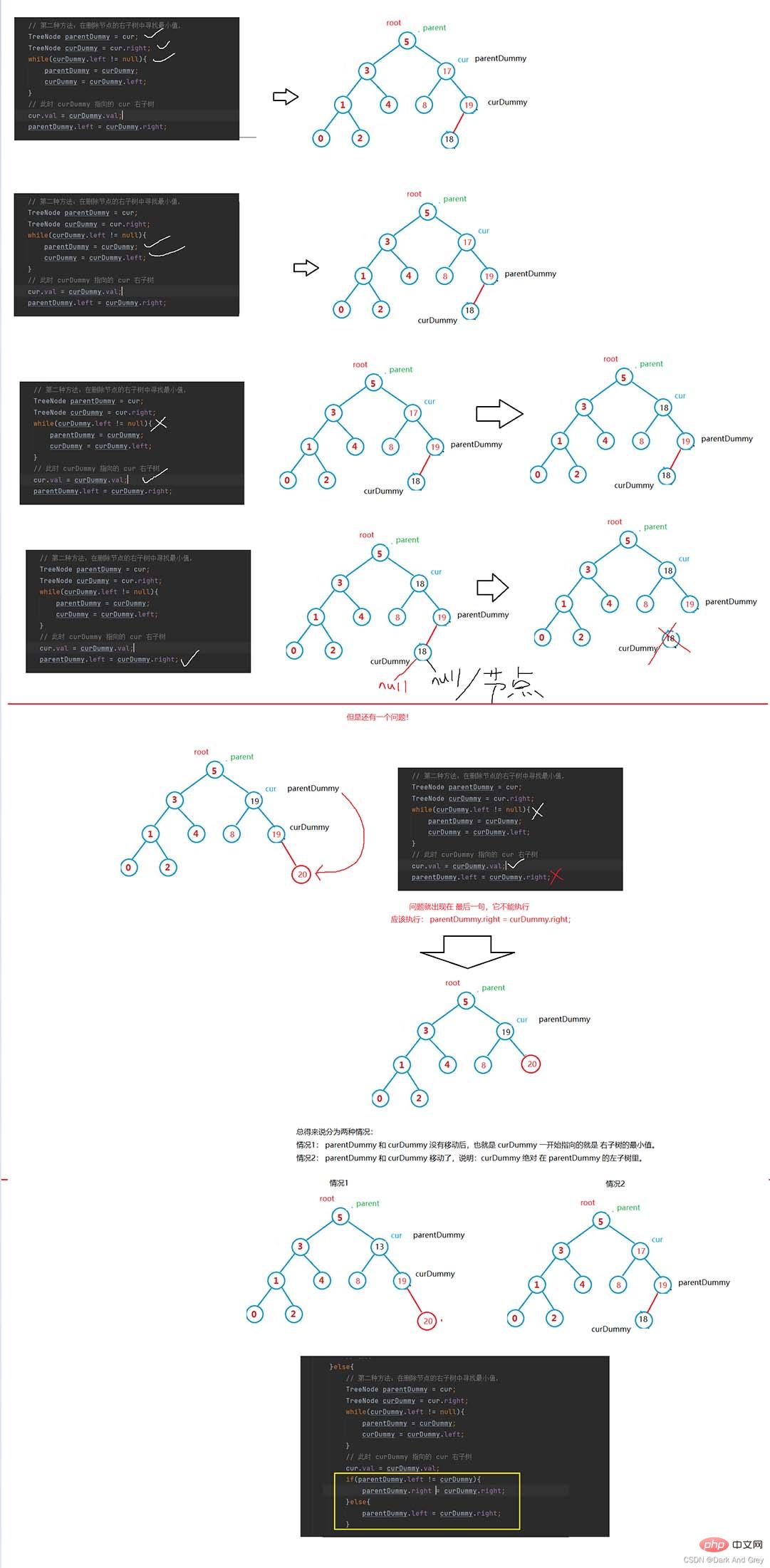
再來分析:curDummy 和parentDummy 是怎麼找到「替罪羊」的。
class TreeNode{
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val){
this.val = val;
}
}
public class BinarySearchTree {
TreeNode root;
//在二叉树中 寻找指定 val 值的节点
// 找到了,返回其节点地址;没找到返回 null
public TreeNode search(int key){
TreeNode cur = this.root;
while(cur != null){
if(cur.val == key){
return cur;
}else if(cur.val < key){
cur = cur.right;
}else{
cur = cur.left;
}
}
return null;
}
// 插入操作
public boolean insert(int key){
if(this.root == null){
this.root = new TreeNode(key);
return true;
}
TreeNode cur = this.root;
TreeNode parent = null;
while(cur!=null){
if(key > cur.val){
parent = cur;
cur = cur.right;
}else if(cur.val == key){
return false;
}else{
parent = cur;
cur = cur.left;
}
}
TreeNode node = new TreeNode(key);
if(parent .val > key){
parent.left = node;
}else{
parent.right = node;
}
return true;
}
// 删除操作
public void remove(int key){
TreeNode cur = root;
TreeNode parent = null;
// 寻找 删除节点位置。
while(cur!=null){
if(cur.val == key){
removeNode(cur,parent);// 真正删除节点的代码
break;
}else if(cur.val < key){
parent = cur;
cur = cur.right;
}else{
parent = cur;
cur = cur.left;
}
}
}
// 辅助删除方法:真正删除节点的代码
private void removeNode(TreeNode cur,TreeNode parent){
// 情况一
if(cur.left == null){
if(cur == this.root){
this.root = this.root.right;
}else if( cur == parent.left){
parent.left = cur.right;
}else{
parent.right = cur.right;
}
// 情况二
}else if(cur.right == null){
if(cur == this.root){
this.root = root.left;
}else if(cur == parent.left){
parent.left = cur.left;
}else{
parent.right = cur.left;
}
// 情况三
}else{
// 第二种方法:在删除节点的右子树中寻找最小值,
TreeNode parentDummy = cur;
TreeNode curDummy = cur.right;
while(curDummy.left != null){
parentDummy = curDummy;
curDummy = curDummy.left;
}
// 此时 curDummy 指向的 cur 右子树
cur.val = curDummy.val;
if(parentDummy.left != curDummy){
parentDummy.right = curDummy.right;
}else{
parentDummy.left = curDummy.right;
}
}
}
// 中序遍历
public void inorder(TreeNode root){
if(root == null){
return;
}
inorder(root.left);
System.out.print(root.val+" ");
inorder(root.right);
}
public static void main(String[] args) {
int[] array = {10,8,19,3,9,4,7};
BinarySearchTree binarySearchTree = new BinarySearchTree();
for (int i = 0; i < array.length; i++) {
binarySearchTree.insert(array[i]);
}
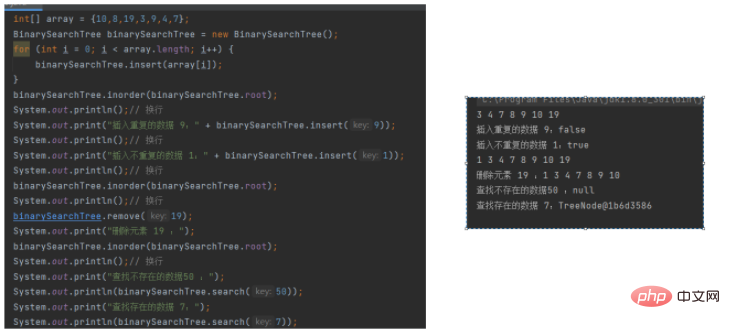
binarySearchTree.inorder(binarySearchTree.root);
System.out.println();// 换行
System.out.print("插入重复的数据 9:" + binarySearchTree.insert(9));
System.out.println();// 换行
System.out.print("插入不重复的数据 1:" + binarySearchTree.insert(1));
System.out.println();// 换行
binarySearchTree.inorder(binarySearchTree.root);
System.out.println();// 换行
binarySearchTree.remove(19);
System.out.print("删除元素 19 :");
binarySearchTree.inorder(binarySearchTree.root);
System.out.println();// 换行
System.out.print("查找不存在的数据50 :");
System.out.println(binarySearchTree.search(50));
System.out.print("查找存在的数据 7:");
System.out.println(binarySearchTree.search(7));
}
}
插入和刪除操作都必須先查找,查找效率代表了二叉搜尋樹中各個操作的效能。
對有n個結點的二元搜尋樹,若每個元素查找的機率相等,則二叉搜尋樹平均查找長度是結點在二叉搜尋樹的深度的函數,即結點越深,則比較次數越多。
但對於同一個關鍵碼集合,如果各關鍵碼插入的次序不同,可能得到不同結構的二元搜尋樹:如果我們能保證二元搜尋樹的左右子樹高度差不超過1。盡量滿足高度平衡條件。
這就變成 AVL 樹了(高度平衡的二元搜尋樹)。而AVL樹,也有缺點:需要一個頻繁的旋轉。浪費很多效率。
至此 紅黑樹就誕生了,避免更多的旋轉。
TreeMap 和TreeSet 即java 中利用搜尋樹實現的Map 和Set;實際上用的是紅黑樹,而紅黑樹是一棵近似平衡的二元搜尋樹,即在二元搜尋樹的基礎之上顏色以及紅黑樹性質驗證,關於紅黑樹的內容,等博主學了,會寫博客的。
以上是Java二元搜尋樹實例分析的詳細內容。更多資訊請關注PHP中文網其他相關文章!




