演算法效率分析分為兩種:第一種是時間效率,第二種是空間效率。時間效率稱為時間複雜度,而空間效率被 稱為空間複雜度。時間複雜度主要衡量的是一個演算法的運行速度,而空間複雜度主要衡量一個演算法所需的額 外空間,在電腦發展的早期,電腦的儲存容量很小。所以對空間複雜度很在乎。但是經過電腦產業的 迅速發展,電腦的儲存容量已經達到了很高的程度。所以我們如今已經不需要再特別重視一個演算法的空間複 雜度。
一個演算法所花費的時間與其中語句的執行次數成正比例,演算法中的基本操作的執行次數,為演算法的時間複雜度。也就是說當我們拿到一個程式碼,來看這個程式碼的時間複雜度的時候,主要是去找這個程式碼當中執行語句次數最多的程式碼執行了多少次。
看圖分析:

#當N的值越來越大,2N和10的值就可以忽略不記了。
實際中我們計算時間複雜度時,我們其實不一定要計算精確的執行次數,而只需要大概執行次數,那麼這裡 我們使用大O的漸進表示法。
大O符號(Big O notation):是用來描述函數漸進式的數學符號。
1、用常數1取代運行時間中的所有加法常數。
2、在修改後的運行次數函數中,只保留最高階項。
3、如果最高階項存在且不是1,則去除與這個項目相乘的常數。得到的結果就是大O階。

透過上面我們會發現大O的漸進表示法去掉了那些對結果影響不大的項,簡潔明了的表示出了執行次數。
另外有些演算法的時間複雜度存在最好、平均和最壞情況:
最壞情況:任意輸入規模的最大運行次數(上界)
#平均情況:任意輸入規模的期望運行次數
最佳情況:任意輸入規模的最小運行次數(下界)
例如:在長度為N數組中搜尋一個資料x
最好情況:1次找到
最壞情況:N次找到
平均情況:N/2次找到
在實際中一般情況關注的是演算法最壞的運作情況,所以在陣列中搜尋資料時間複雜度為O(N)
範例1:

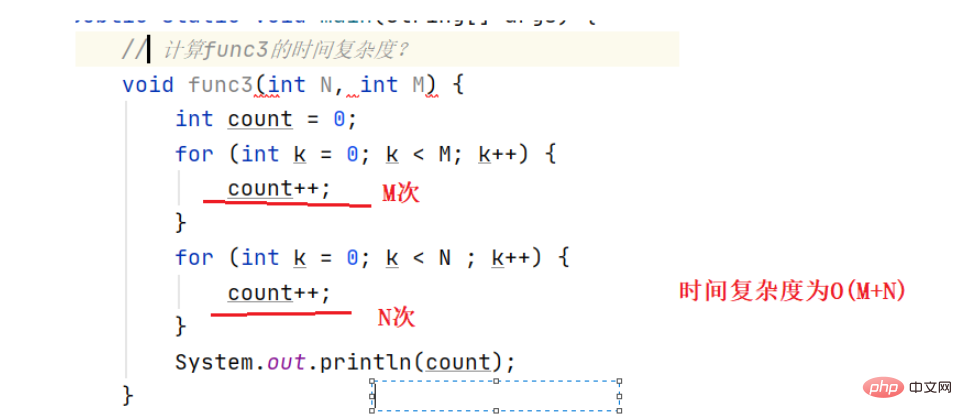
 # #基本運算執行了100次,透過推導大O階方法,時間複雜度為O(1)
# #基本運算執行了100次,透過推導大O階方法,時間複雜度為O(1)
#例題4:計算冒泡排序的時間複雜度
 基本運算執行最好N次,最壞執行了(N*(N-1))/2次,透過推導大O階方法時間複雜度一般看最壞, 時間複雜度為O( N^2
基本運算執行最好N次,最壞執行了(N*(N-1))/2次,透過推導大O階方法時間複雜度一般看最壞, 時間複雜度為O( N^2
例題5:二分查找的時間複雜度
 #基本運算執行最好1次,最壞O(logN)次,時間複雜度為O(logN) ps:logN在演算法分析中表示是底數為2,對數為N。有些地方會寫成lgN。(建議透過摺紙查找的方式講解logN是怎麼計算出來的)(因為二分查找每次排除掉一半的不適合值,一次二分剩下:n/2 兩次二分剩下:n/2/2 = n/4)
#基本運算執行最好1次,最壞O(logN)次,時間複雜度為O(logN) ps:logN在演算法分析中表示是底數為2,對數為N。有些地方會寫成lgN。(建議透過摺紙查找的方式講解logN是怎麼計算出來的)(因為二分查找每次排除掉一半的不適合值,一次二分剩下:n/2 兩次二分剩下:n/2/2 = n/4)
例題6:計算階乘遞歸的時間複雜度
遞歸的時間複雜度= 遞歸的次數*每次遞歸執行的次數
 透過計算分析發現基本運算遞歸了N次,時間複雜度為O(N)。
透過計算分析發現基本運算遞歸了N次,時間複雜度為O(N)。
範例7:計算斐波那契遞歸的時間複雜度
透過計算分析發現基本操作遞歸了2^N次,時間複雜度為O(2^N)。
規律:
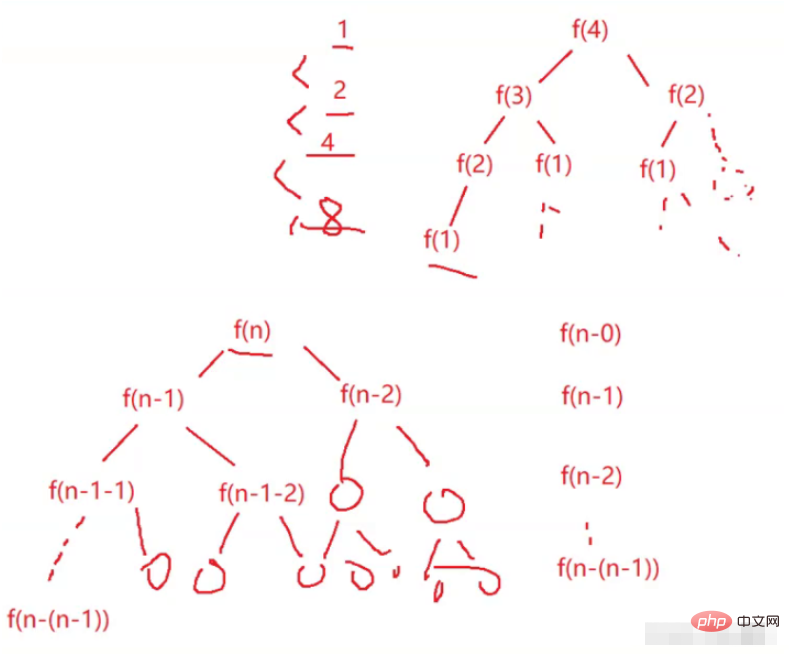
2^0 2^1 2^2 2^3……2^(n-(n-1))
等比數列求和
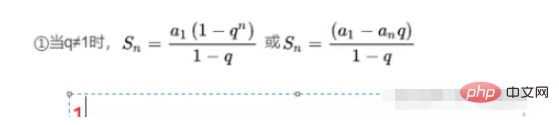
a1就代表第一項,q是等比就是2,1(1-2^n)/-1 ,相當於2^n 1,所以時間複雜度為O(2^n)
空間複雜度是對一個演算法在運行過程中暫時佔用存儲空間大小的量度。空間複雜度不是程式佔用了多少bytes 的空間,因為這個也沒太大意義,所以空間複雜度算的是變數的數量。空間複雜度計算規則基本上跟實踐複雜度 類似,也使用大O漸進表示法。
範例1:計算冒泡排序的空間複雜度
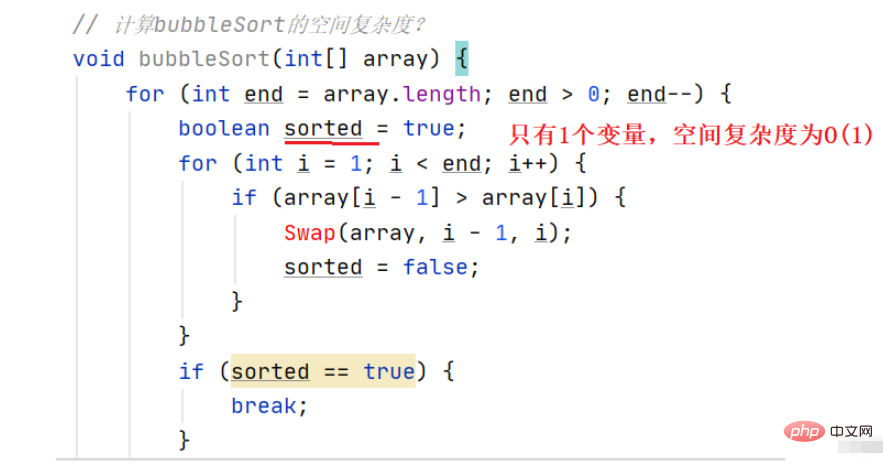
#使用了常數個額外空間,所以空間複雜度為O(1)
範例2:計算斐波那契的空間複雜度
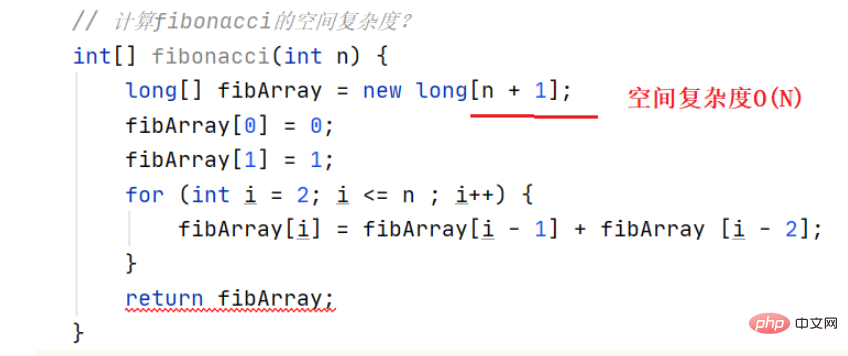
動態開啟了N個空間,空間複雜度為O(N)
例題3:計算階乘遞歸的空間複雜度

遞歸呼叫了N次,開啟了N個堆疊幀,每個堆疊幀使用了常數個空間。空間複雜度為O(N)
以上是Java時間複雜度與空間複雜度實例分析的詳細內容。更多資訊請關注PHP中文網其他相關文章!




