利用統計測試和機器學習分析和預測太陽能發電的性能測試和對比
本文將討論透過使用假設測試、特徵工程、時間序列建模方法等從資料集中獲得有形價值的技術。我還將解決不同時間序列模型的資料外洩和資料準備等問題,並且對常見的三種時間序列預測進行對比測試。
時間序列預測是一個經常被研究的議題,我們在這裡使用使用兩個太陽能電站的數據,研究其規律進行建模。首先將它們歸納為兩個問題來解決這些問題:
在繼續回答這些問題之前,讓我們先了解太陽能發電廠是如何發電的。
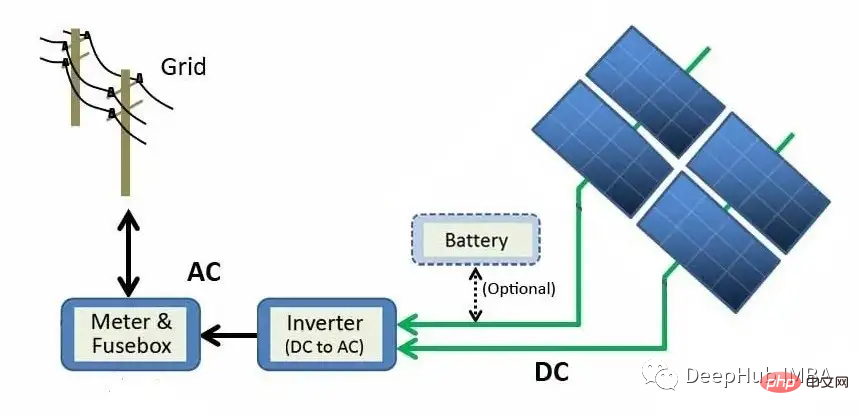
上圖描述了從太陽能板模組到電網的發電過程。太陽能透過光電效應直接轉換為電能。當矽(太陽能板中最常見的半導體材料)等材料暴露在光線下時,光子(電磁能量的亞原子粒子)被吸收並釋放自由電子,從而產生直流電(DC)。使用逆變器,直流電被轉換成交流電(AC)並發送到電網,在那裡它可以被分配到家庭。
原始資料由每個太陽能發電廠的兩個逗號分隔值(CSV)檔案組成。一份文件顯示了發電過程,另一份文件顯示了太陽能發電廠感測器記錄的測量數據。每個太陽能發電廠的兩個資料集都被整理成一個pandas的df。
太陽能發電廠1號(SP1)和太陽能發電廠2號(SP2)的資料每15分鐘收集一次,從2020年5月15日到2020年6月18日。 SP1和SP2資料集都包含相同的變數。
天氣感測器用於記錄每個太陽能發電廠的環境溫度、組件溫度和輻射。
對於這個資料集直流功率將是因變數(目標變數)。我們目標是的試圖找到性能不佳的太陽能模組。
兩個獨立的df用於分析和預測。唯一的差異是用於預測的資料被重新採樣為每小時的間隔,而用於分析的資料幀包含15分鐘的間隔。
首先我們刪除Plant ID,因為它對試圖回答上述問題沒有任何價值。 Module ID也從預測資料集中刪除。表1和表2顯示了數據範例。


在繼續分析資料之前,我們對太陽能發電廠做了一些假設,包括:
對於資料科學的新手來說,EDA是透過繪圖視覺化和執行統計測試來理解資料的關鍵一步。我們首先透過繪製SP1和SP2的DC和AC,可以觀察到每個太陽能發電廠的表現。
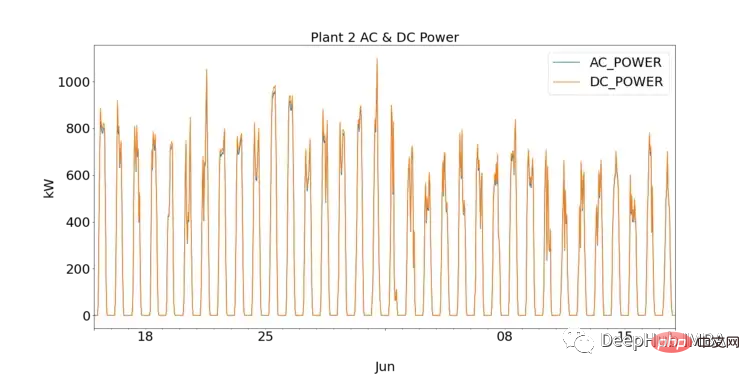
SP1顯示的直流功率比sp2高一個數量級。假設SP1所擷取的資料是正確的,用於記錄資料的儀器沒有故障,這表示SP1中逆變器需要更深入的研究
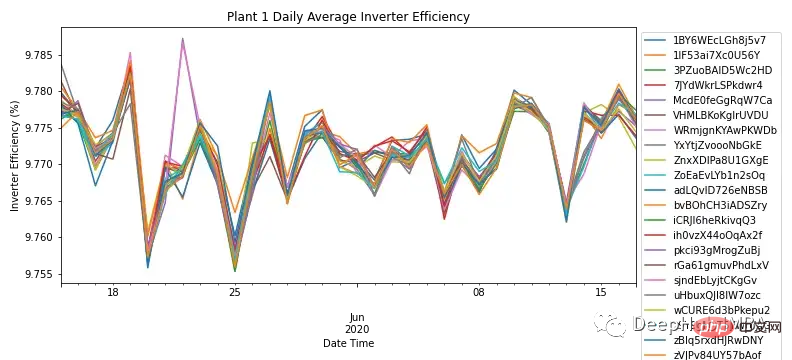
透過每個模組的日頻率聚合AC和DC功率,圖3顯示了SP1中所有模組的逆變器效率。根據領域內知識,太陽能逆變器的效率應在93-96%之間。由於所有模組的效率範圍為9.76% - 9.79%,這裡可以說明需要調查逆變器的性能,以及是否需要更換。
由於SP1顯示了逆變器的問題,因此僅在SP2上進行了進一步的分析。
儘管這一小段分析是我們花了更多的時間對逆變器進行研究,但它並沒有回答確定太陽能模組性能的主要問題。
由於SP2的逆變器正常運作,可以透過深入挖掘數據,來識別和調查任何異常情況。
圖4中顯示了模組溫度和環境溫度之間的關係,並且有模組溫度極高的情況。
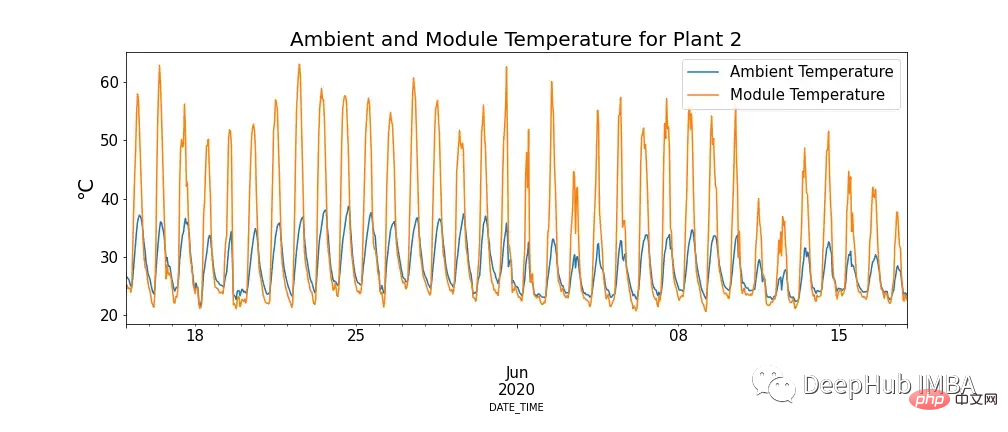
這看起來似乎違反我們的認知,但是可以看到高溫對太陽能板的確有負面影響。當光子與太陽能電池內的電子接觸時,它們會釋放自由電子,但在更高的溫度下,更多的電子已經處於激發態,這降低了電池板可以產生的電壓,進而降低了效率。
考慮到這一現象,下面的圖5顯示了SP2的模組溫度和直流功率(環境溫度低於模組溫度的資料點和模組運行數量較少的一天中的時間已經過過濾,以防止資料傾斜)。
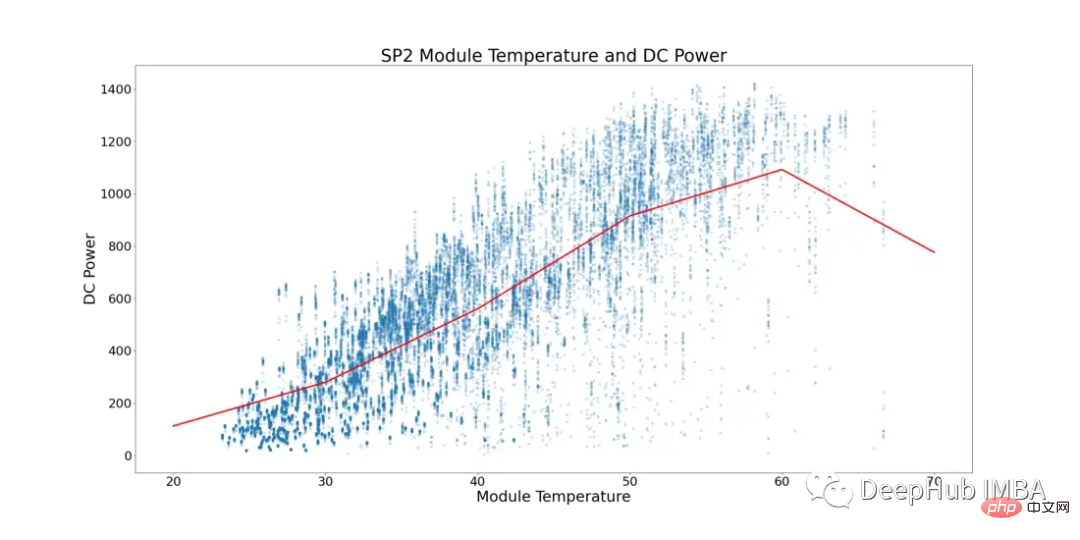
在圖5中,紅線表示平均溫度。這裡可以看到有一個明確的臨界點和直流電源停滯的跡象。在~52°C開始平穩。為了找到性能次優的太陽能模組,所有顯示模組溫度超過52°C的行都被刪除。
下面的圖6顯示了SP2中每個模組在一天中的直流功率。這樣基本上就符合了預期,午間發電量較大。但還有個問題,在運作高峰時期,發電量較低。我們很難總結造成這種情況的原因,因為當天的天氣條件可能很差,或者SP2可能需要日常的維護等等。
圖6中也有低效能模組的跡象。它們可以被辨識為圖上偏離最近群集的模組(單一資料點)。

為了確定哪些模組表現不佳,我們可以進行統計測試,同時將每個模組的效能與其他模組進行比較,從而確定效能。
每隔15分鐘,不同模組的直流電源在同一時間的分佈是常態分佈,透過假設檢定可以確定哪些模組表現不佳。計數是指模組落在99.9%信賴區間之外且p值
圖7按降序顯示了每個模組在統計上顯著低於同期其他模組的次數。

從圖7可以清楚看出,模組' Quc1TzYxW2pYoWX '是有問題的。這些資訊可以提供給SP2的相關工作人員,調查原因。
下面我們開始使用三種不同的時間序列演算法:SARIMA、XGBoost和CNN-LSTM,進行建模並比較
對於所有三個模型,都使用預測下一個數據點進行預測。 Walk-forward驗證是一種用於時間序列建模的技術,因為隨著時間的推移,預測會變得不那麼準確,因此更實用的方法是在實際資料可用時,用實際資料重新訓練模型。
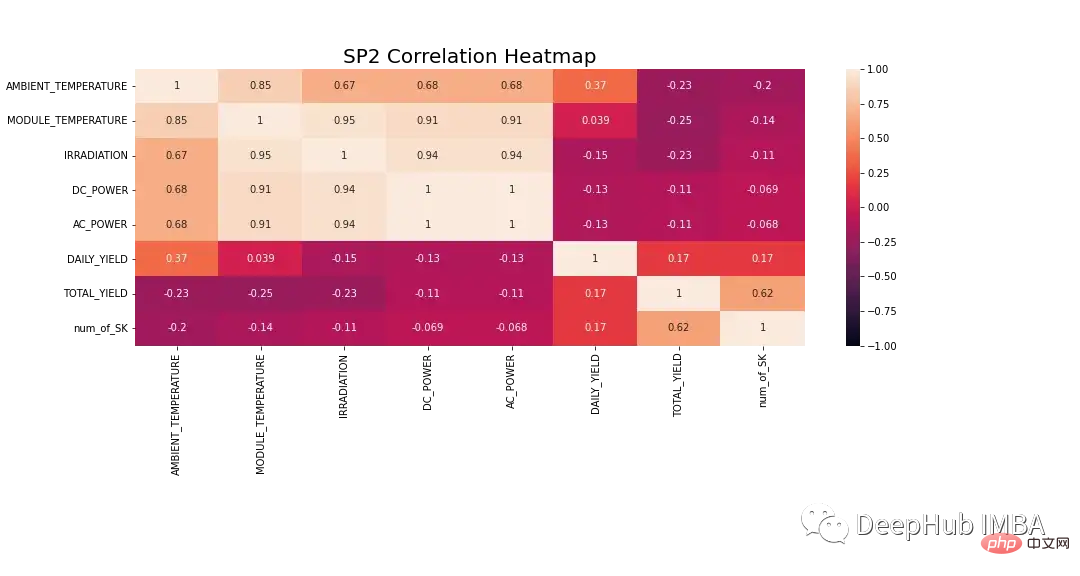
在建模之前需要更詳細地研究資料。圖8顯示了SP2資料集中所有特徵的相關熱圖。熱圖顯示了因變數直流功率,與模組溫度、輻照和環境溫度的強相關性。這些特徵可能在預測中發揮重要作用。
在下面的熱圖中,交流功率顯示皮爾森相關係數為1。為了防止資料外洩問題,我們將直流功率從資料中刪除。
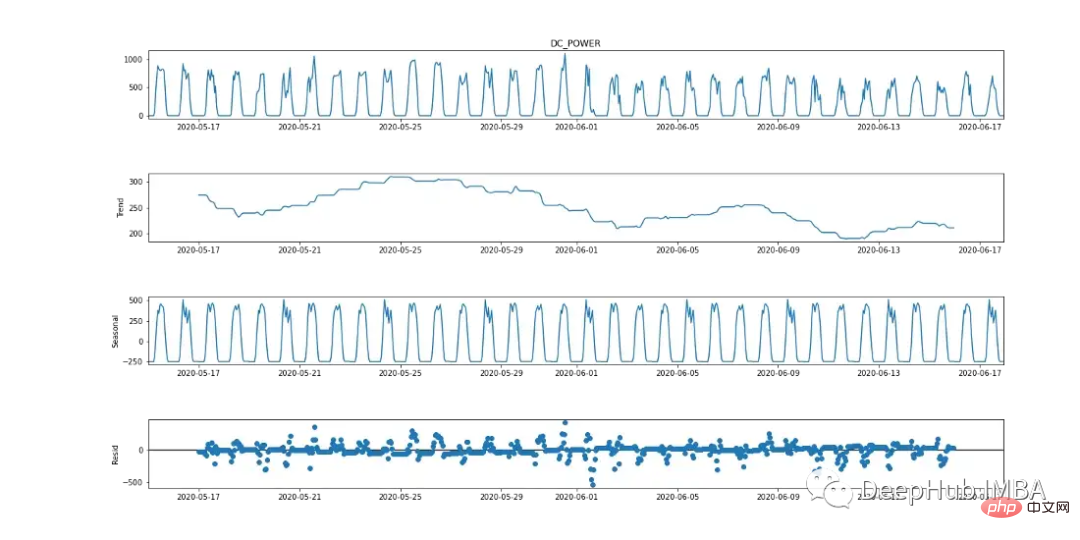
季節自迴歸綜合移動平均(SARIMA)是一種單變量時間序列預測方法。由於目標變數顯示出24小時循環週期的跡象,SARIMA是一個有效的建模選項,因為它考慮了季節影響。這可以從下面的季節分解圖中觀察到。
SARIMA演算法要求資料是平穩的。有許多方法可以檢定資料是否平穩,例如統計檢定(增強迪基-福勒檢定),總結統計(比較資料的不同部分的平均值/變異數)和視覺化分析資料。在建模之前進行多次測試是很重要的。
增強迪基-富勒(ADF)檢定是一種“單位根檢定”,用於確定時間序列是否平穩。從根本上說,這是一個統計顯著性檢驗,其中存在一個零假設和替代假設,並根據得出的p值得出結論。
零假設:時間序列資料是非平穩的。
替代假設:時間序列資料是平穩的。
在我們的例子中,如果p值≤0.05,我們可以拒絕原假設,並確認資料沒有單位根。
from statsmodels.tsa.stattools import adfuller
result = adfuller(plant2_dcpower.values)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
print('t%s: %.3f' % (key, value))
從ADF檢定來看,p值為0.000553,< 0.05。根據這項統計數據,可以認為該數據是穩定的。然而,查看圖2(最上面的圖),有明顯的季節性跡象(對於被認為是平穩的時間序列數據,不應該有季節性和趨勢的跡象),這說明數據是非平穩的。因此,運行多個測試非常重要。 < 0.05。根据这一统计数据,可以认为该数据是稳定的。然而,查看图2(最上面的图),有明显的季节性迹象(对于被认为是平稳的时间序列数据,不应该有季节性和趋势的迹象),这说明数据是非平稳的。因此,运行多个测试非常重要。
為了用SARIMA對因變數建模,時間序列需要是平穩的。如圖9(第一個和第三個圖)所示,直流電有明顯的季節性跡象。取第一個差值[t-(t-1)]去除季節性成分,如圖10所示,因為它看起來類似於常態分佈。數據現在是平穩的,適用於SARIMA演算法。
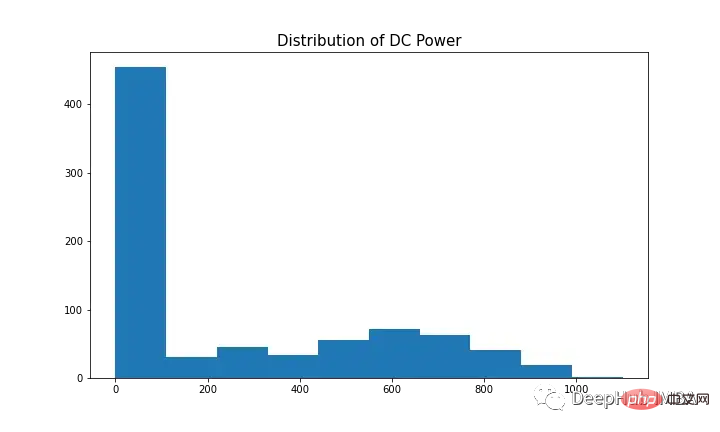
SARIMA的超參數包含p(自迴歸階數)、d(差階數)、q(移動平均階數)、p(季節自迴歸階數)、d(季節差階數)、q(季節移動平均階數)、m(季節週期的時間步長)、trend(確定性趨勢)。
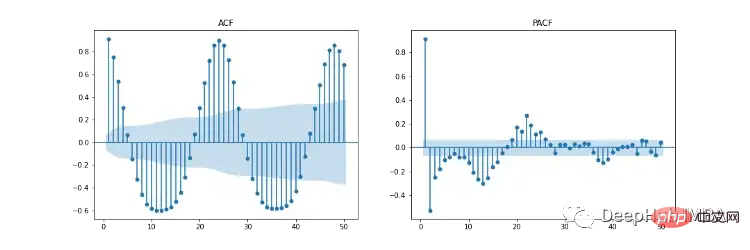
圖11顯示了自相關(ACF)、部分自相關(PACF)和季節性ACF/PACF圖。 ACF圖顯示了時間序列與其延遲版本之間的相關性。 PACF顯示了時間序列與其滯後版本之間的直接相關性。藍色陰影區域表示信賴區間。 SACF和SPACF可以透過從原始資料中取季節差(m)來計算,在本例中為24,因為在ACF圖中有一個明顯的24小時的季節效應。
根據我們的直覺,超參數的起點可以從ACF和PACF圖中推導出來。如ACF和PACF均呈現逐漸下降的趨勢,即自回歸階數(p)和移動平均階數(q)均大於0。 p和p可以透過分別觀察PCF和SPCF圖,並計算滯後值不顯著之前具有統計顯著性的滯後數來確定。同樣,q和q可以在ACF和SACF圖中找到。
差階(d)可以透過使資料平穩的差的數量來確定。季節差異階數(D)是根據從時間序列中去除季節性成分所需的差異數來估計的。
這些超參數選擇可以看這篇文章:https://arauto.readthedocs.io/en/latest/how_to_choose_terms.html
也可以採用網格搜尋方法進行超參數最佳化,根據最小均方誤差(MSE)選擇最優超參數,包括p = 2, d = 0, q = 4, p = 2, d = 1, q = 6, m = 24, trend = ' n '(無趨勢)。
from time import time
from sklearn.metrics import mean_squared_error
from statsmodels.tsa.statespace.sarimax import SARIMAX
configg = [(2, 1, 4), (2, 1, 6, 24), 'n']
def train_test_split(data, test_len=48):
"""
Split data into training and testing.
"""
train, test = data[:-test_len], data[-test_len:]
return train, test
def sarima_model(data, cfg, test_len, i):
"""
SARIMA model which outputs prediction and model.
"""
order, s_order, t = cfg[0], cfg[1], cfg[2]
model = SARIMAX(data, order=order, seasonal_order=s_order, trend=t,
enforce_stationarity=False, enfore_invertibility=False)
model_fit = model.fit(disp=False)
yhat = model_fit.predict(len(data))
if i + 1 == test_len:
return yhat, model_fit
else:
return yhat
def walk_forward_val(data, cfg):
"""
A walk forward validation technique used for time series data. Takes current value of x_test and predicts
value. x_test is then fed back into history for the next prediction.
"""
train, test = train_test_split(data)
pred = []
history = [i for i in train]
test_len = len(test)
for i in range(test_len):
if i + 1 == test_len:
yhat, s_model = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
mse = mean_squared_error(test, pred)
return pred, mse, s_model
else:
yhat = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
history.append(test[i])
pass
if __name__ == '__main__':
start_time = time()
sarima_pred_plant2, sarima_mse, s_model = walk_forward_val(plant2_dcpower, configg)
time_len = time() - start_time
print(f'SARIMA runtime: {round(time_len/60,2)} mins')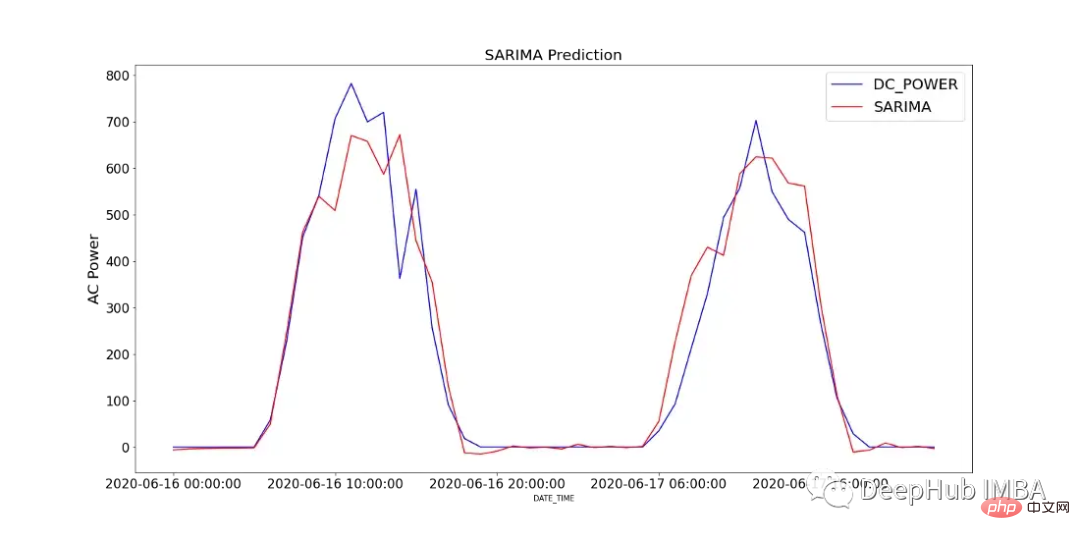
圖12顯示了SARIMA模型的預測值與SP2 2天內所記錄的直流功率的比較。
為了分析模型的效能,圖13顯示了模型診斷。相關圖顯示在第一個滯後後幾乎沒有相關性,下面的直方圖顯示在平均值為零附近的常態分佈。由此我們可以說模型無法從數據中收集到進一步的資訊。
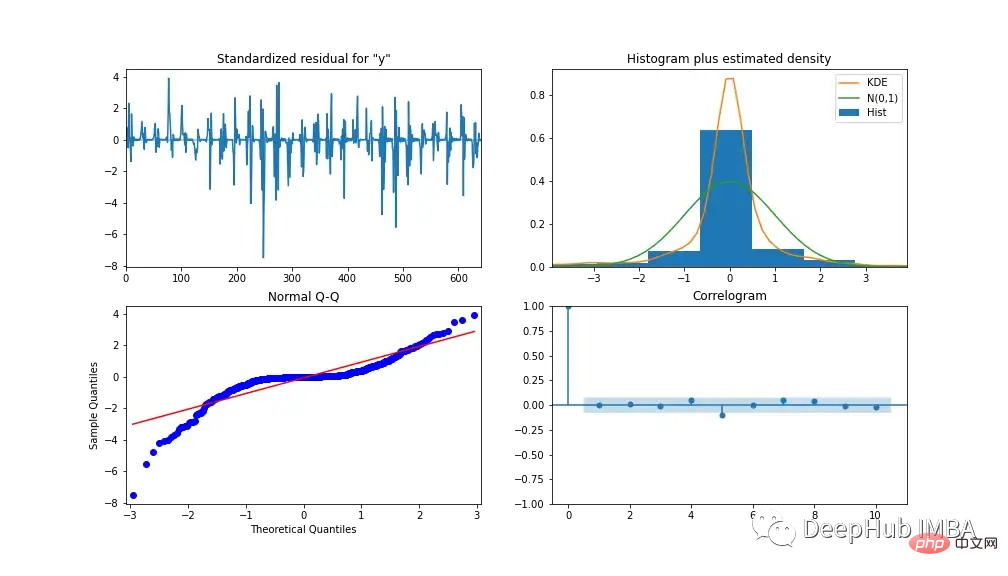
XGBoost (eXtreme Gradient Boosting)是一種梯度增強決策樹演算法。它使用整合方法,其中添加新的決策樹模型來修改現有的決策樹分數。與SARIMA不同的是,XGBoost是一種多元機器學習演算法,這意味著該模型可以採用多特徵來提高模型效能。
我們採用特徵工程提高模型精度。也創建了3個附加特性,其中包括AC和DC功率的滯後版本,分別為S1_AC_POWER和S1_DC_POWER,以及透過交流功率除以直流功率的整體效率EFF。並將AC_POWER和MODULE_TEMPERATURE從資料中刪除。圖14透過增益(使用一個特徵的分割的平均增益)和權重(一個特徵在樹中出現的次數)顯示了特徵的重要性等級。

透過網格搜尋確定建模使用的超參數,結果為:*learning rate = 0.01, number of estimators = 1200, subsample = 0.8, colsample by tree = 1, colsample by level = 1, min child weight = 20 and max depth = 10
我們使用MinMaxScaler將訓練資料縮放到0到1之間(也可以試驗其他縮放器,如log-transform和standard-scaler,這取決於數據的分佈)。透過將所有自變數向後移動一段時間,將資料轉換為監督學習資料集。
import numpy as np
import pandas as pd
import xgboost as xgb
from sklearn.preprocessing import MinMaxScaler
from time import time
def train_test_split(df, test_len=48):
"""
split data into training and testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
def data_to_supervised(df, shift_by=1, target_var='DC_POWER'):
"""
Convert data into a supervised learning problem.
"""
target = df[target_var][shift_by:].values
dep = df.drop(target_var, axis=1).shift(-shift_by).dropna().values
data = np.column_stack((dep, target))
return data
def xgb_forecast(train, x_test):
"""
XGBOOST model which outputs prediction and model.
"""
x_train, y_train = train[:,:-1], train[:,-1]
xgb_model = xgb.XGBRegressor(learning_rate=0.01, n_estimators=1500, subsample=0.8,
colsample_bytree=1, colsample_bylevel=1,
min_child_weight=20, max_depth=14, objective='reg:squarederror')
xgb_model.fit(x_train, y_train)
yhat = xgb_model.predict([x_test])
return yhat[0], xgb_model
def walk_forward_validation(df):
"""
A walk forward validation approach by scaling the data and changing into a supervised learning problem.
"""
preds = []
train, test = train_test_split(df)
scaler = MinMaxScaler(feature_range=(0,1))
train_scaled = scaler.fit_transform(train)
test_scaled = scaler.transform(test)
train_scaled_df = pd.DataFrame(train_scaled, columns = train.columns, index=train.index)
test_scaled_df = pd.DataFrame(test_scaled, columns = test.columns, index=test.index)
train_scaled_sup, test_scaled_sup = data_to_supervised(train_scaled_df), data_to_supervised(test_scaled_df)
history = np.array([x for x in train_scaled_sup])
for i in range(len(test_scaled_sup)):
test_x, test_y = test_scaled_sup[i][:-1], test_scaled_sup[i][-1]
yhat, xgb_model = xgb_forecast(history, test_x)
preds.append(yhat)
np.append(history,[test_scaled_sup[i]], axis=0)
pred_array = test_scaled_df.drop("DC_POWER", axis=1).to_numpy()
pred_num = np.array([pred])
pred_array = np.concatenate((pred_array, pred_num.T), axis=1)
result = scaler.inverse_transform(pred_array)
return result, test, xgb_model
if __name__ == '__main__':
start_time = time()
xgb_pred, actual, xgb_model = walk_forward_validation(dropped_df_cat)
time_len = time() - start_time
print(f'XGBOOST runtime: {round(time_len/60,2)} mins')图15显示了XGBoost模型的预测值与SP2 2天内记录的直流功率的比较。
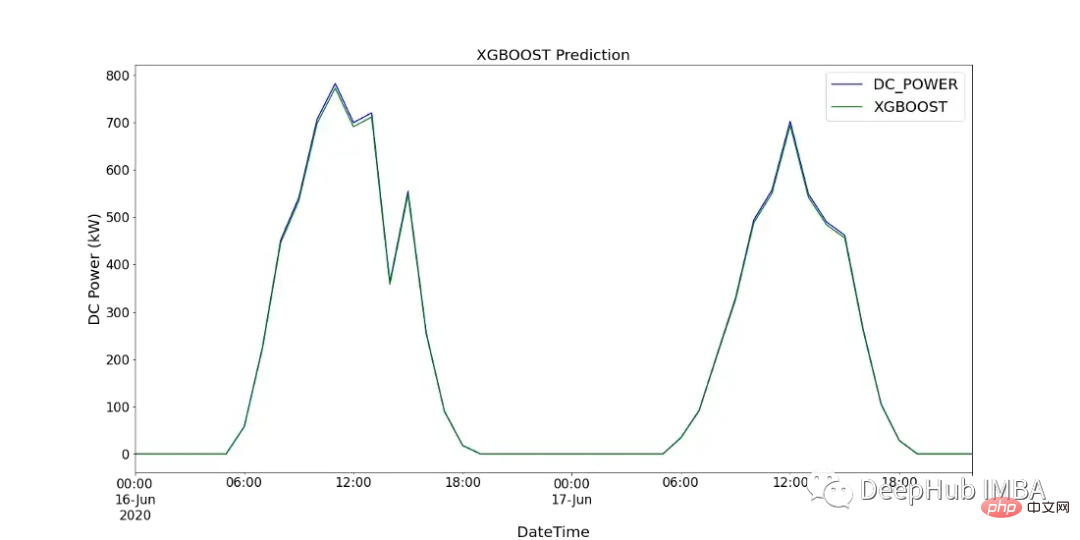
CNN-LSTM (convolutional Neural Network Long - Short-Term Memory)是两种神经网络模型的混合模型。CNN是一种前馈神经网络,在图像处理和自然语言处理方面表现出了良好的性能。它还可以有效地应用于时间序列数据的预测。LSTM是一种序列到序列的神经网络模型,旨在解决长期存在的梯度爆炸/消失问题,使用内部存储系统,允许它在输入序列上积累状态。
在本例中,使用CNN-LSTM作为编码器-解码器体系结构。由于CNN不直接支持序列输入,所以我们通过1D CNN读取序列输入并自动学习重要特征。然后LSTM进行解码。与XGBoost模型类似,使用scikitlearn的MinMaxScaler使用相同的数据并进行缩放,但范围在-1到1之间。对于CNN-LSTM,需要将数据重新整理为所需的结构:[samples, subsequences, timesteps, features],以便可以将其作为输入传递给模型。
由于我们希望为每个子序列重用相同的CNN模型,因此使用timedidistributedwrapper对每个输入子序列应用一次整个模型。在下面的图16中可以看到最终模型中使用的不同层的模型摘要。
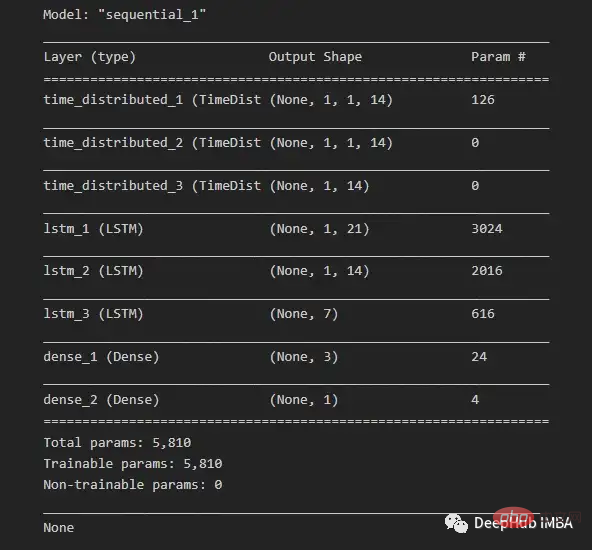
在将数据分解为训练数据和测试数据之后,将训练数据分解为训练数据和验证数据集。在所有训练数据(包括验证数据)的每次迭代之后,模型可以进一步使用这一点来评估模型的性能。
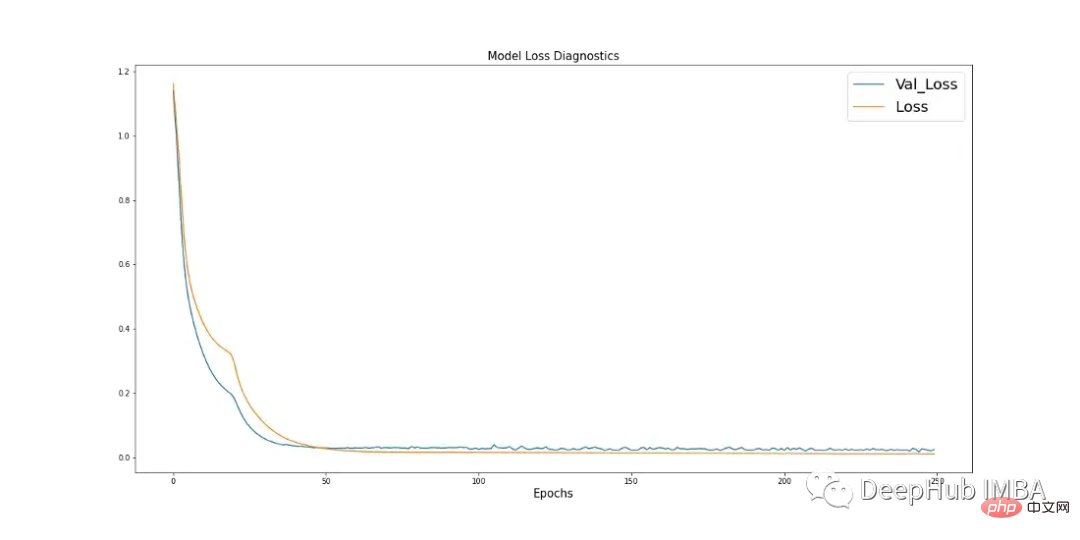
学习曲线是深度学习中使用的一个很好的诊断工具,它显示了模型在每个阶段之后的表现。下面的图17显示了模型如何从数据中学习,并显示了验证数据与训练数据的收敛。这是良好模特训练的标志。
import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
import keras
from keras.models import Sequential
from keras.layers.convolutional import Conv1D, MaxPooling1D
from keras.layers import LSTM, TimeDistributed, RepeatVector, Dense, Flatten
from keras.optimizers import Adam
n_steps = 1
subseq = 1
def train_test_split(df, test_len=48):
"""
Split data in training and testing. Use 48 hours as testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
def split_data(sequences, n_steps):
"""
Preprocess data returning two arrays.
"""
x, y = [], []
for i in range(len(sequences)):
end_x = i + n_steps
if end_x > len(sequences):
break
x.append(sequences[i:end_x, :-1])
y.append(sequences[end_x-1, -1])
return np.array(x), np.array(y)
def CNN_LSTM(x, y, x_val, y_val):
"""
CNN-LSTM model.
"""
model = Sequential()
model.add(TimeDistributed(Conv1D(filters=14, kernel_size=1, activation="sigmoid",
input_shape=(None, x.shape[2], x.shape[3]))))
model.add(TimeDistributed(MaxPooling1D(pool_size=1)))
model.add(TimeDistributed(Flatten()))
model.add(LSTM(21, activation="tanh", return_sequences=True))
model.add(LSTM(14, activation="tanh", return_sequences=True))
model.add(LSTM(7, activation="tanh"))
model.add(Dense(3, activation="sigmoid"))
model.add(Dense(1))
model.compile(optimizer=Adam(learning_rate=0.001), loss="mse", metrics=['mse'])
history = model.fit(x, y, epochs=250, batch_size=36,
verbose=0, validation_data=(x_val, y_val))
return model, history
# split and resahpe data
train, test = train_test_split(dropped_df_cat)
train_x = train.drop(columns="DC_POWER", axis=1).to_numpy()
train_y = train["DC_POWER"].to_numpy().reshape(len(train), 1)
test_x = test.drop(columns="DC_POWER", axis=1).to_numpy()
test_y = test["DC_POWER"].to_numpy().reshape(len(test), 1)
#scale data
scaler_x = MinMaxScaler(feature_range=(-1,1))
scaler_y = MinMaxScaler(feature_range=(-1,1))
train_x = scaler_x.fit_transform(train_x)
train_y = scaler_y.fit_transform(train_y)
test_x = scaler_x.transform(test_x)
test_y = scaler_y.transform(test_y)
# shape data into CNN-LSTM format [samples, subsequences, timesteps, features] ORIGINAL
train_data_np = np.hstack((train_x, train_y))
x, y = split_data(train_data_np, n_steps)
x_subseq = x.reshape(x.shape[0], subseq, x.shape[1], x.shape[2])
# create validation set
x_val, y_val = x_subseq[-24:], y[-24:]
x_train, y_train = x_subseq[:-24], y[:-24]
n_features = x.shape[2]
actual = scaler_y.inverse_transform(test_y)
# run CNN-LSTM model
if __name__ == '__main__':
start_time = time()
model, history = CNN_LSTM(x_train, y_train, x_val, y_val)
prediction = []
for i in range(len(test_x)):
test_input = test_x[i].reshape(1, subseq, n_steps, n_features)
yhat = model.predict(test_input, verbose=0)
yhat_IT = scaler_y.inverse_transform(yhat)
prediction.append(yhat_IT[0][0])
time_len = time() - start_time
mse = mean_squared_error(actual.flatten(), prediction)
print(f'CNN-LSTM runtime: {round(time_len/60,2)} mins')
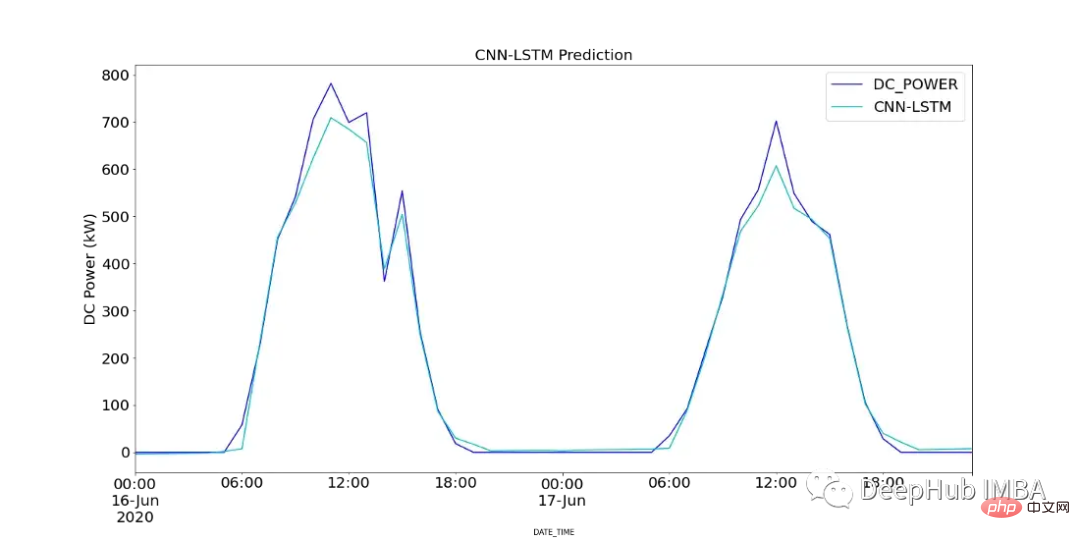
print(f"CNN-LSTM MSE: {round(mse,2)}")图18显示了CNN-LSTM模型的预测值与SP2 2天内记录的直流功率的对比。
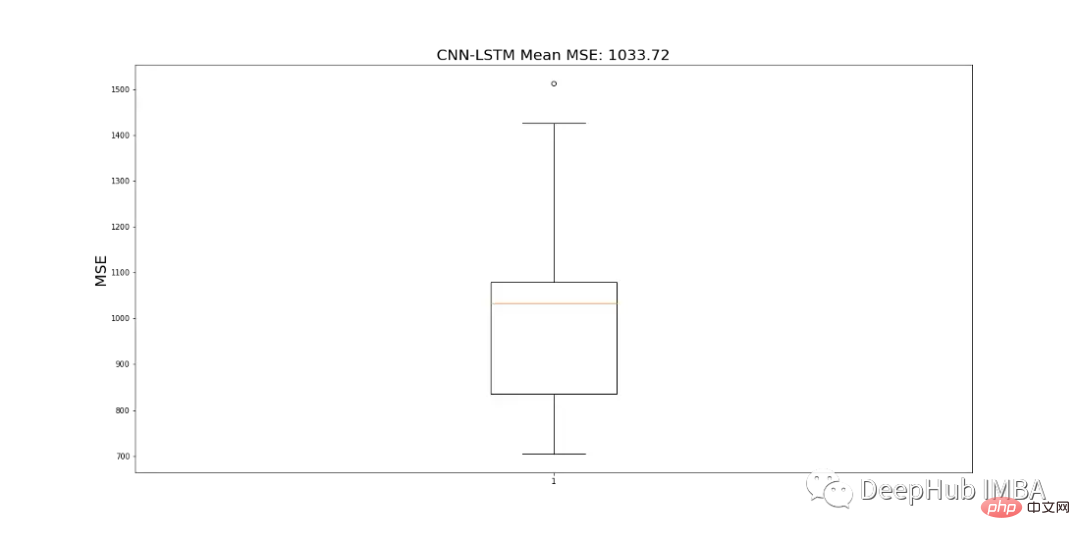
由于CNN-LSTM的随机性,该模型运行10次,并记录一个平均MSE值作为最终值,以判断模型的性能。图19显示了为所有模型运行记录的mse的范围。
下表显示了每个模型的MSE (CNN-LSTM的平均MSE)和每个模型的运行时间(以分钟为单位)。
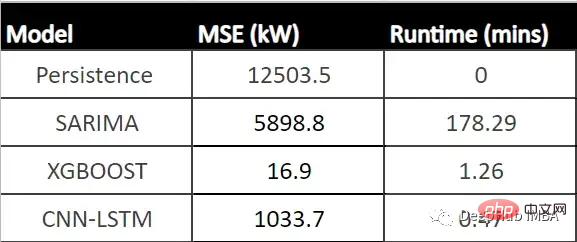
从表中可以看出,XGBoost的MSE最低、运行时第二快,并且与所有其他模型相比具有最佳性能。由于该模型显示了一个可以接受的每小时预测的运行时,它可以成为帮助运营经理决策过程的强大工具。
在本文中我们分析了SP1和SP2,确定SP1性能较低。所以对SP2的进一步调查显示,并且查看了SP2中那些模块性能可能有问题,并使用假设检验来计算每个模块在统计上明显表现不佳的次数,' Quc1TzYxW2pYoWX '模块显示了约850次低性能计数。
我们使用数据训练三个模型:SARIMA、XGBoost和CNN-LSTM。SARIMA表现最差,XGBOOST表现最好,MSE为16.9,运行时间为1.43 min。所以可以说XGBoost在表格数据中还是最优先得选择。
以上是比較基於SARIMA、XGBoost和CNN-LSTM的時間序列預測方法。的詳細內容。更多資訊請關注PHP中文網其他相關文章!




