
線性迴歸通常是人們為機器學習和資料科學學習的第一個演算法。它簡單易懂,但是由於其功能有限,在實際業務中並不是最佳選擇。大多數情況下,線性迴歸被用作基準模型來評估和比較研究中的新方法。
在處理實際問題時,我們應該了解並嘗試過許多其他迴歸演算法。在本文中,將透過使用Scikit-learn和 XGBoost 的動手練習來學習 9 種流行的回歸演算法。本文的架構如下:
本次資料使用的是一個藏在Python第三方vega_datasets模組中的著名的資料科學公開數據集。
vega_datasets裡的數據集內容挺多,有統計數據也有地理數據,還有不同數據量的版本,例如flights數據集包含了2k、5k、200k、3m等多個版本。
呼叫是寫:df = data('iris')或df = data.iris(),資料存在在Anaconda3/Lib/site-packages/vega_datasets目錄下,存本地的在local_datasets.json裡有描述。本機存的有csv格式的也有json格式的。
df = data.cars()
df.head()
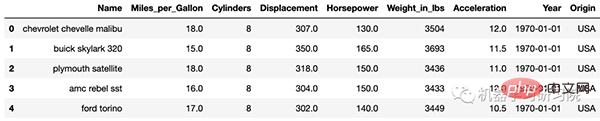
df.info()
class 'pandas.core.frame.DataFrame'>
RangeIndex: 406 entries, 0 to 405
Data columns (total 9 columns):
# ColumnNon-Null CountDtype
----------------------------
0 Name406 non-nullobject
1 Miles_per_Gallon398 non-nullfloat64
2 Cylinders 406 non-nullint64
3 Displacement406 non-nullfloat64
4 Horsepower400 non-nullfloat64
5 Weight_in_lbs 406 non-nullint64
6 Acceleration406 non-nullfloat64
7 Year406 non-nulldatetime64[ns]
8 Origin406 non-nullobject
dtypes: datetime64[ns](1 "ns"), float64(4), int64(2), object(2)
memory usage: 28.7+ KB
# 过滤特定列中的NaN行
df.dropna(subset=['Horsepower', 'Miles_per_Gallon'], inplace=True)
df.sort_values(by='Horsepower', inplace=True)
# 数据转换
X = df['Horsepower'].to_numpy().reshape(-1, 1)
y = df['Miles_per_Gallon'].to_numpy().reshape(-1, 1)
plt.scatter(X, y, color='teal', edgecolors='black', label='Horsepower vs. Miles_per_Gallon')
plt.legend()
plt.show()
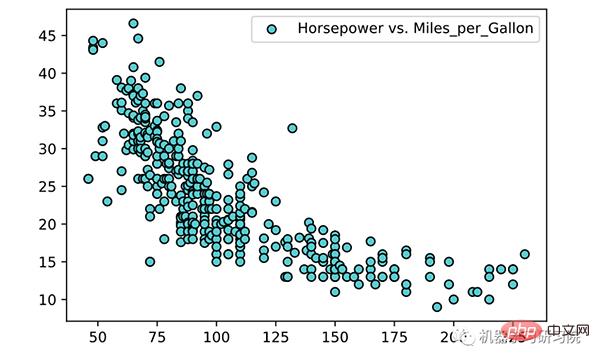
線性迴歸通常學習機器學習與資料科學的第一個演算法。線性迴歸是一種線性模型,它假設輸入變數 ( X) 和單一輸出變數 ( y)之間存在線性關係。一般來說,有兩種情況:
這個演算法很常見,Scikit-learn[2]內建簡單線性迴歸LinearRegression()演算法。接下來就和小猴子一起創建一個LinearRegression對象,並使用訓練資料進行訓練。
from sklearn.linear_model import LinearRegression # 创建和训练模型
linear_regressor = LinearRegression()
linear_regressor.fit(X, y)
訓練完成後,可以使用LinearRegression的coef_屬性中查看模型係數參數:
linear_regressor.coef_
array([[-0.15784473]])
現在使用訓練好的模型並為訓練資料擬合一條線。
# 为训练数据绘制点和拟合线
plt.scatter(X, y, color='RoyalBlue', edgecolors='black', label='Horsepower vs. Miles_per_Gallon')
plt.plot(X, linear_regressor.predict(X), color='orange', label='Linear regressor')
plt.title('Linear Regression')
plt.legend()
plt.show()
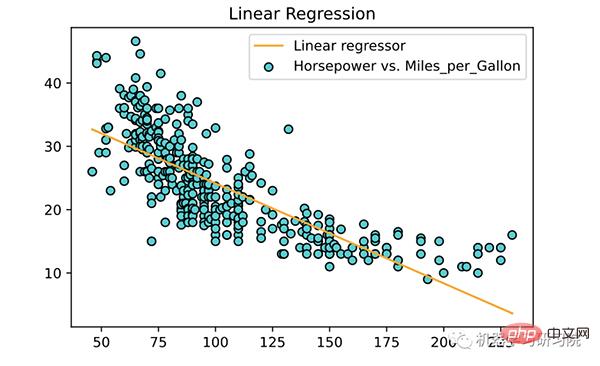
關於線性迴歸的幾個關鍵點:
當想要為非線性可分資料建立模型時,多項式迴歸是最受歡迎的選擇之一。它類似於線性迴歸,但使用變數X和y之間的關係並為資料點找到繪製適合曲線的最佳方法。
對於多項式迴歸,有些自變數的冪大於 1。例如,可能提出以下的二次模型:
Scikit-learn內建多項式迴歸PolynomialFeatures。首先,我們需要產生一個由所有具有指定次數的多項式特徵組成的特徵矩陣:
from sklearn.preprocessing import PolynomialFeatures
# 为二次模型生成矩阵
# 这里只是简单地生成X^0 X^1和X^2的矩阵
poly_reg = PolynomialFeatures(degree = 2 )
X_poly = poly_reg.fit_transform(X)
接下來,讓我們建立一個LinearRegression物件並將其擬合到X_poly我們剛剛產生的特徵矩陣中。
# 多项式回归模型
poly_reg_model = LinearRegression()
poly_reg_model.fit(X_poly, y)
現在採用該模型並為訓練資料擬合一條線,X_plot如下所示:
# 为训练数据绘制点和拟合线
plt.scatter(X, y, color='DarkTurquoise', edgecolors='black',
label='Horsepower vs. Miles_per_Gallon')
plt.plot(X, poly_reg_model.predict(X_poly), color='orange',
label='Polynmial regressor')
plt.title('Polynomial Regression')
plt.legend()
plt.show()
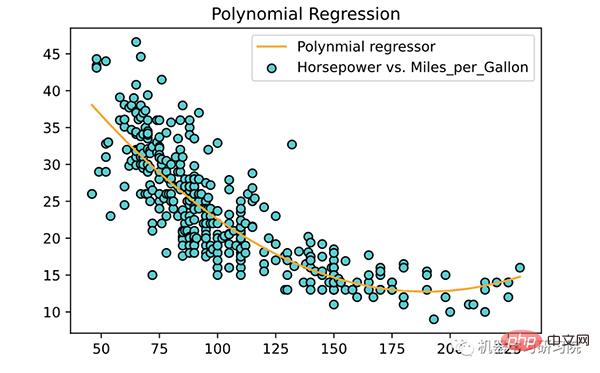
關於多項式回歸的幾個關鍵點:
众所周知的支持向量机在处理分类问题时非常有效。其实,SVM 也经常用在回归问题中,被称为支持向量回归(SVR)。同样,Scikit-learn内置了这种方法SVR()。
在拟合 SVR 模型之前,通常较好的做法是对数据进行数据标准化操作,及对特征进行缩放。数据标准化的目的是为了确保每个特征都具有相似的重要性。我们通过StandardScaler()方法对训练数据操作。
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler # 执行特征缩放
scaled_X = StandardScaler()
scaled_y = StandardScaler()
scaled_X = scaled_X.fit_transform(X)
scaled_y = scaled_y.fit_transform(y)
接下来,我们创建了一个SVR与对象的内核设置为'rbf'和伽玛设置为'auto'。之后,我们调用fit()使其适合缩放的训练数据:
svr_regressor = SVR(kernel='rbf', gamma='auto')
svr_regressor.fit(scaled_X, scaled_y.ravel())
现在采用该模型并为训练数据拟合一条线,scaled_X如下所示:
plt.scatter(scaled_X, scaled_y, color='DarkTurquoise',
edgecolors='black', label='Train')
plt.plot(scaled_X, svr_regressor.predict(scaled_X),
color='orange', label='SVR')
plt.title('Simple Vector Regression')
plt.legend()
plt.show()
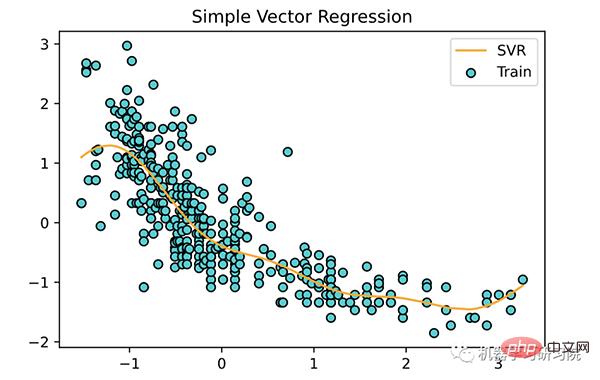
支持向量回归的几个关键点
决策树 (DT) 是一种用于分类和回归的非参数监督学习方法 。目标是创建一个树模型,通过学习从数据特征推断出的简单决策规则来预测目标变量的值。一棵树可以看作是分段常数近似。
决策树回归也很常见,以至于Scikit-learn内置了DecisionTreeRegressor. 甲DecisionTreeRegressor对象可以在没有特征缩放如下创建:
from sklearn.tree import DecisionTreeRegressor
# 不需要进行特性缩放,因为它将自己处理。
tree_regressor = DecisionTreeRegressor(random_state = 0)
tree_regressor.fit(X, y)
下面使用训练好的模型,绘制一条拟合曲线。
X_grid = np.arange(min(X), max(X), 0.01)
X_grid = X_grid.reshape(len(X_grid), 1)
plt.scatter(X, y, color='DarkTurquoise',
edgecolors='black', label='Train')
plt.plot(X_grid, tree_regressor.predict(X_grid),
color='orange', label='Tree regressor')
plt.title('Tree Regression')
plt.legend()
plt.show()
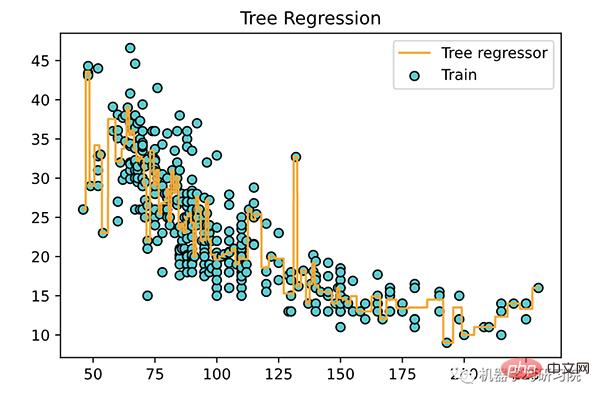
关于决策树的几个关键点:
一般地,随机森林回归与决策树回归非常相似,它是一个元估计器,在数据集的各种子样本集上拟合许多决策树,并使用平均方法来提高预测准确性和控制过拟合。
随机森林回归器在回归中的性能可能比决策树好,也可能不比决策树好(虽然它通常在分类中表现更好),因为树构造算法本质上存在微妙的过度拟合-欠拟合权衡。
随机森林回归很常见,以至于Scikit-learn内置了RandomForestRegressor. 首先,我们需要创建一个RandomForestRegressor具有指定数量估计器的对象,如下所示:
from sklearn.ensemble import RandomForestRegressor
forest_regressor = RandomForestRegressor(
n_estimators = 300,
random_state = 0
)
forest_regressor.fit(X, y.ravel())
下面使用训练好的模型,绘制一条拟合曲线。
X_grid = np.arange(min(X), max(X), 0.01)
X_grid = X_grid.reshape(len(X_grid), 1)
plt.scatter(X, y, color='DarkTurquoise',
edgecolors='black', label='Train')
plt.plot(X_grid, forest_regressor.predict(X_grid),
color='orange', label='Random Forest regressor')
plt.title('Random Forest Regression')
plt.legend()
plt.show()
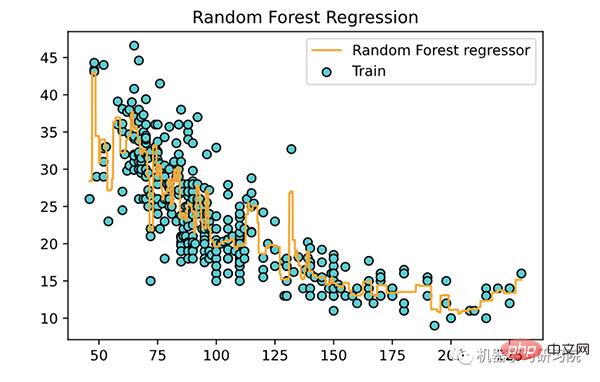
关于随机森林回归的几个关键点:
LASSO 回归是使用收缩的线性回归的变体。收缩是数据值向中心点收缩作为均值的过程。这种类型的回归非常适合显示重度多重共线性(特征彼此之间的重度相关性)的模型。
Scikit-learn内置了LassoCV.
from sklearn.linear_model import LassoCV
lasso = LassoCV()
lasso.fit(X, y.ravel())
下面使用训练好的模型,绘制一条拟合曲线。
plt.scatter(X, y, color='teal', edgecolors='black',
label='Actual observation points')
plt.plot(X, lasso.predict(X), color='orange',
label='LASSO regressor')
plt.title('LASSO Regression')
plt.legend()
plt.show()
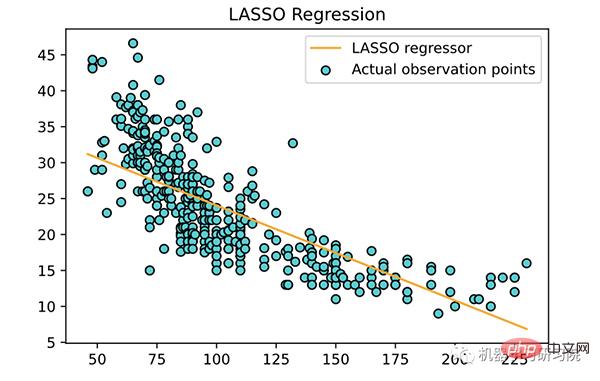
关于套索回归的几点:
岭回归与 LASSO 回归非常相似,因为这两种技术都使用收缩。Ridge 回归和 LASSO 回归都非常适合显示重度多重共线性(特征彼此之间的高度相关性)的模型。它们之间的主要区别在于 Ridge 使用 L2 正则化,这意味着没有一个系数像在 LASSO 回归中那样变为零(而是接近零)。
Scikit-learn内置了RidgeCV.
from sklearn.linear_model import RidgeCV
ridge = RidgeCV()
ridge.fit(X, y)
下面使用训练好的模型,绘制一条拟合曲线。
plt.scatter(X, y, color='teal', edgecolors='black',
label='Train')
plt.plot(X, ridge.predict(X), color='orange',
label='Ridge regressor')
plt.title('Ridge Regression')
plt.legend()
plt.show()
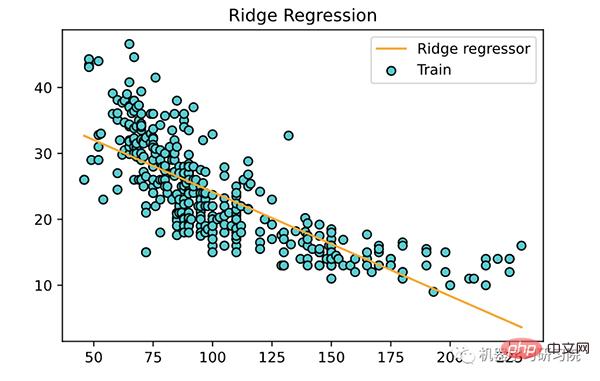
关于岭回归的几个关键点:
ElasticNet 是另一个使用 L1 和 L2 正则化训练的线性回归模型。它是 LASSO 和岭回归技术的混合体,因此它也非常适合显示严重多重共线性(特征彼此高度相关)的模型。
Lasso 和 Ridge 之间权衡的一个实际优势是它允许 Elastic-Net 在旋转时继承一些 Ridge 的稳定性。
Scikit-learn内置了ElasticNetCV模型.
from sklearn.linear_model import ElasticNetCV
elasticNet = ElasticNetCV()
elasticNet.fit(X, y.ravel())
下面使用训练好的模型,绘制一条拟合曲线。
plt.scatter(X, y, color='DarkTurquoise', edgecolors='black', label='Train')
plt.plot(X, elasticNet.predict(X), color='orange',label='ElasticNet regressor')
plt.title('ElasticNet Regression')
plt.legend()
plt.show()
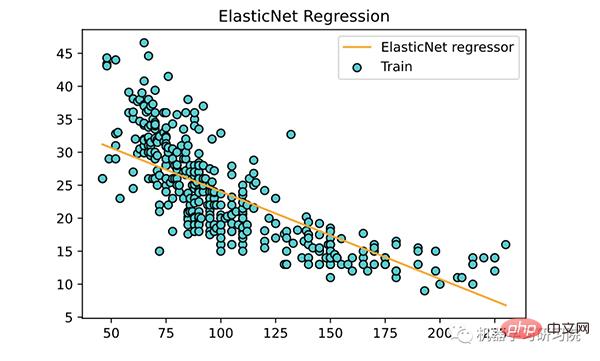
ElasticNet 回归的几个关键点:
极限梯度提升( XGBoost ) 是梯度提升算法的高效实现。梯度提升是指一类可用于分类或回归问题的集成机器学习算法。
XGBoost是由最初开发的开放源码库tianqi-chen[3]在他的题为“2016论文XGBoost:可扩展树增压系统[4]”。该算法被设计为具有计算效率和高效性。
第一步是安装 XGBoost 库(如果尚未安装)。
pip install xgboost
可以通过创建以下实例来定义 XGBoost 模型XGBRegressor:
from xgboost import XGBRegressor
# create an xgboost regression model
model = XGBRegressor(
n_estimators=1000,
max_depth=7,
eta=0.1,
subsample=0.7,
colsample_bytree=0.8,
)
下面使用训练好的模型,绘制一条拟合曲线。
plt.scatter(X, y, color='DarkTurquoise', edgecolors='black', label='Train')
plt.plot(X, model.predict(X), color='orange',label='XGBoost regressor')
plt.title('XGBoost Regression')
plt.legend()
plt.show()
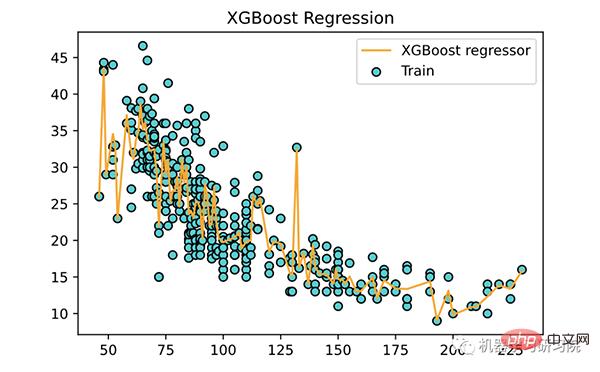
关于 XGBoost 的几个关键点:
到这里本文就结束啦,本文我们通过使用Scikit-learn和 XGBoost 的动手实践介绍了 九种流行的回归算法。在解决实际问题时,可以尝试不同的算法并找到解决实际问题的最佳回归模型。
以上是九種頂流迴歸演算法及實例總結的詳細內容。更多資訊請關注PHP中文網其他相關文章!




