JavaScript中Number型別常見迷思背後原理及解決方法-js教程-PHP中文網

這篇文章為大家帶來了關於JavaScript的相關知識，其中主要介紹了關於number類型的相關知識，包括了number類型的常見誤區背後原理以及解決方法等內容，下面一起來看一下，希望對大家有幫助。

JavaScript中Number型別常見迷思背後原理及解決方法

在JavaScript 中數值只有一種，即Number 類型，內部表示為雙精度浮點型，即其他語言中的double 類型，所以在JavaScript 中實際上是沒有整數類型的，數值都是按浮點數來處理的，存儲方法相同，遵循IEEE 754 國際標準。因此，在JavaScript 中3 和3.0 被視為同一個值：

3.0 === 3 // true

登入後複製

對於整數情況，能夠準確計算的整數範圍為在−253-2^{53}−253 ~ 2532^{53} 253 之間，不包含兩個端點，只要在這個範圍內整數可以放心使用。除了十進制以外整數還可以透過八進位或十六進制的字面值來表示，其中八進製字面值的第一位必須為零，其次是八進制數字序列（0 ~ 7），如果字面值中的數值超出範圍，那麼前導零將被忽略，後面的數值被當作十進制解析，這兒需要注意在嚴格模式中八進制的這種表示會報錯，ES6中進一步明確，八進制的表示要使用前綴0o，示例：

(function(){
  console.log(0o11 === 011)
})()
// true
// 严格模式
(function(){
  &#39;use strict&#39;;
  console.log(0o11 === 011)
})()
// Uncaught GyntaxError

登入後複製

十六進位字面值前兩位必須是0x，後面接著任何十六進位數字（0 ~ 9以及A ~ F）,其中A ~ F 可以大寫，也可以小寫。 ES6中又擴展了二進位的寫法，使用前綴0b（或0B）。

前面我們對JavaScript 執行時期中的Number 類型進行了簡單介紹，接下來正式開始介紹這些常見問題，不過首先我們需要了解Number 類型的資料儲存方式：

一、儲存方式

JavaScript 中的Number 類型使用的是雙精度浮點型，即其他語言中的double 類型，雙精度浮點數使用8 個位元組即64bit 來進行存儲，現代計算機中浮點數大多是以國際標準IEEE 754 來存儲，存儲過程分兩步，

#把浮點數轉換為對應的二進制數，並用科學計數法表示
#將轉換之後的數字透過IEEE 754 標準表示成真正會在電腦儲存的值。

根據IEEE 754 標準任何一個二進位浮點數V 都可以表示成：

JavaScript中Number型別常見迷思背後原理及解決方法

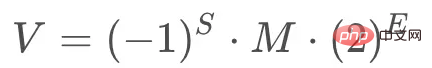
#舉個例子，十進制的5.0，寫成二進位是101.0，相當於1.01∗221.01 * 2^21.01∗22，其中S=0，M=1.01，E=2。

IEEE 754規定對於32位元浮點數最高1位元是符號位元S，接下來8位元是指數E，剩下的23位元為有效數字M，如下圖所示：

JavaScript中Number型別常見迷思背後原理及解決方法

對於64位元的浮點數最高1位元是符號位元S，接下來11位元是指數E，剩下的52位元是有效數字M，如下圖所示：

JavaScript中Number型別常見迷思背後原理及解決方法

注意：IEEE754 對於有效數字M和指數E還有一些特別的規定。

前面說過，1 <= M < 2，也就是說 M 總是可以寫成 1.xxxxxxx 的形式，其中 xxxxxxx 表示效數部分。 IEEE 754 規定，在電腦內部儲存 M 時預設這個數的第一位總是1，因此可以被捨去，只保存後面的 xxxxxxx 部分。例如儲存1.01的時候只存01，等到讀取的時候再把第一位的1加上去，這樣做的目的就是為了節省一位有效數字，以32位浮點數為例，留給有效數字M的只有23位，將第一位的1捨去以後等於保存24位有效數字。

至於指數E，情況較為複雜。首先，E為一個無符號指數，這意味著，如果E為8位，它的取值範圍為 0 ~ 255，如果E為11位，它的取值範圍為0 ~ 2047。但是我們知道科學計數中的E是可以出現負值的，所以IEEE 754規定，E的真實值必須再減去一個中間數，對於8位的E，這個中間數是127，對於11位的E ，這個中間數是1023。

例如2102^{10}210的E是10，所以儲存成32位元浮點數時，必須儲存成 10 127=137，即 10001001。

然後指數E還可以分成三種情況：

E不全为0或不全为1：这时，浮点数就采用上面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第一位的1。
E全为0：这时，浮点数的指数E等于1 ~ 127（或1 ~ 1023），有效数字M不再加上第一位的1，而是还原成0.xxxxxxx的小数，这样做是为了表示±0，以及接近0的很小的数字。
E全为1：这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位S）；如果有效数字M不全为0，表示这个数不是一个数（NaN）。

示例：浮点数 9.0 如何用二进制表示？还原成十进制又是多少？

首先，浮点数 9.0 等于二进制的 1001.0，即 1.001∗231.001 *2^31.001∗23

那么，第一位的符号位 S=0，有效数字 M 等于 001 后面再加 20 个 0，凑满 23 位，指数 E 等于 3+127=130，即 10000010。

所以，写成二进制形式，应该是 S+E+M，即0 10000010 001 0000 0000 0000 0000 0000。这个 32 位的二进制数，还原成十进制，正是 1091567616。

注：虽然在 JavaScript 中无论是小数还是整数都是按照64位的浮点数形式存储，但是进行整数运算会自动转换为32位的有符号整数，例如位运算，有符号整数使用31位表示整数的数值，用第32位表示整数的符号，数值范围是−231-2^{31}−231 ~ 2312^{31}231。

二、浮点数运算的精度丢失

问题缘由

众所周知在 JavaScript 中 0.1+0.2 不等于 0.3，实际上所有浮点数值存储遵循 IEEE 754 标准的编程语言中都会存在这个问题，这是因为计算机中小数的存储先是转换成二进制进行存储的，而 0.1、0.2 转换成二进制分别为：

(0.1)10 => (00011001100110011001(1001)...)2 (0.2)10 => (00110011001100110011(0011)...)2

可以发现，0.1 和 0.2 转成二进制之后都是一个无限循环的数，前面提到尾数位只能存储最多 53 位有效数字，这时候就必须来进行四舍五入了，而这个取舍的规则就是在 IEEE 754 中定义的，0.1 最终能被存储的有效数字是

0001(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)101 + (0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)01 = 0100(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)111

最终的这个二进制数转换成十进制的就是 0.30000000000000004 ，这儿需要注意，53 位的存储位指的是能存 53 位有效数字，因此前置的 0 不算，要往后再取到 53 位有效数字为止。

因此，精度丢失的问题实际上用一句话概括就是计算机中用二进制存储小数，而大部分小数转成二进制后都是无限循环的值，因此存在取舍问题，也就是精度丢失。

解决办法

ES6 在 Number 对象上新增了一个极小常量：Number.EPSILON，值为 2.220446049250313e-16，引入这么一个常量就是为了为浮点数计算设置一个误差范围，如果这个误差小于 Number.EPSILON 我们就认为得到了准确结果。

三、大整数的运算精度丢失及溢出

问题缘由

在介绍问题的具体缘由之前我想先给大家介绍一下所谓最大安全整数范围以及最大数字绝对值的范围是如何得到的？

JavaScript 能够表示的数字的绝对值范围是 5e-324 ~ 1.7976931348623157e+308，这两个取值可以通过 Number.MIN_VALUE 和 Number.MAX_VALUE 这两个字段来表示，如果某次计算的结果得到了一个超出 JavaScript 数值范围的，那么这个数值会自动被转换为特殊的 Infinity 值，具体来说，如果这个数是负数，则会被转换成 -Infinity（负无穷），如果这个数值是正数，则会被转换成 Infinity（正无穷）。

示例：

console.log(Number.MAX_VALUE) // 1.7976931348623157e+308
console.log(Number.MIN_VALUE) // 5e-324
console.log(Number.MAX_VALUE + Number.MAX_VALUE) // Infinity

登入後複製

那么这个取值范围是如何得到的呢？

前面说到 JavaScript 中数值的保存采用的是双精度浮点型，遵循 IEEE 754 标准，在 ECMAScript 规范中规定指数 E 的范围在 -1074 ~ 971，双精度浮点型中有效数字 M 的存储位为52，但是有效数字 M 由于可以省略第一位1，节省一个存储位，因此有效数字M可以存储的范围为 1 ~ 2532^{53}253，因此 JavaScript 中 Number 能表示的最大数字绝对值范围是 2−10742^{-1074}2−1074 ~ 253+9712^{53+971}253+971。

注：通过 Number.isFinite()（ES6引入）和 isFinite() 方法可以判断一个数值是不是有穷的，即如果参数位于最小与最大数值之间时会返回 true。

让我们回归主题，为什么会出现大整数的运算精度丢失及溢出呢？

JavaScript 中最大安全整数的范围是 −253-2^{53}−253 ~ 2532^{53}253，不包括两个端点，即 -9007199254740991 ~ 9007199254740991，可以通过 Number.MIN_SAFE_INTEGER 和 Number.MAX_SAFE_INTEGER 字段查询，超出这个范围的整数计算都是不准确的，例如：

console.log(Number.MAX_SAFE_INTEGER) // 9007199254740991
console.log(Number.MIN_SAFE_INTEGER) // -9007199254740991
console.log(9007199254740991 + 2) // 9007199254740992

登入後複製

最大安全整数9007199254740991对应的二进制数如图：

JavaScript中Number型別常見迷思背後原理及解決方法

53位有效数字都存储满了之后，想要表示更大的数字，就只能往指数数加一位，这时候尾数因为没有多余的存储空间，因此只能补0。

JavaScript中Number型別常見迷思背後原理及解決方法

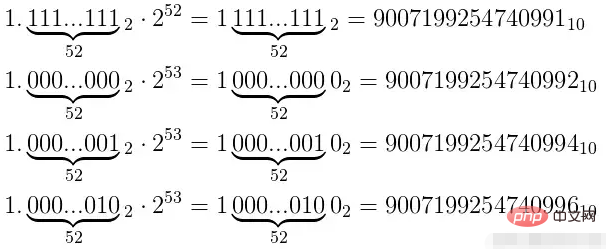
如图所示，在指数位为53的情况下，最后一位尾数位为0的数字可以被精确表示，而最后一位尾数位为1的数字都不能被精确表示。也就是可以被精确表示和不能被精确表示的比例是1:1。

同理，当指数为54的时候，只有最后两位尾数为00的可以被精确表示，也就是可以被精确表示和不能被精确表示的比例是1:3，当有效位数达到 x(x>53) 的时候，可以被精确表示和不能被精确表示的比例将是1 : 2^(x-53)^ - 1。

可以预见的是，在指数越来越高的时候，这个指数会成指数增长，因此在 Number.MAX_SAFE_INTEGER ~ Number.MAX_VALUE 之间可以被精确表示的整数可以说是凤毛麟角。

之所以会有最大安全整数这个概念，本质上还是因为数字类型在计算机中的存储结构。在尾数位不够补零之后，只要是多余的尾数为1所对应的整数都不能被精确表示。

可以发现，不管是浮点数计算的计算结果错误和大整数的计算结果错误，最终都可以归结到JS的精度只有53位（尾数只能存储53位的有效数字）。

解决办法

那么我们在日常工作中碰到这两个问题该如何解决呢？

大而全的解决方案就是使用 mathjs，看一下 mathjs 的输出：

math.config({
    number: &#39;BigNumber&#39;,      
    precision: 64 
});
console.log(math.format(math.eval(&#39;0.1 + 0.2&#39;))); // &#39;0.3&#39;
console.log(math.format(math.eval(&#39;0.23 * 0.34 * 0.92&#39;))); // &#39;0.071944&#39;
console.log(math.format(math.eval(&#39;9007199254740991 + 2&#39;))); 
// &#39;9.007199254740993e+15&#39;

登入後複製

【相关推荐：JavaScript视频教程、web前端】

以上是JavaScript中Number型別常見迷思背後原理及解決方法的詳細內容。更多資訊請關注PHP中文網其他相關文章！