本篇文章為大家帶來了關於python的相關知識,其中主要介紹了雙端隊列的相關問題,包括了雙端隊列的基本概念、雙端隊列的實現以及雙端隊列的應用,希望對大家有幫助。

推薦學習:python教程
雙端佇列是另一個線性數據結構。雖然它也是一種受限線性表,但與堆疊和佇列不同的是,雙端佇列的限制很少,它的基本操作也是線性表操作的子集,但從資料類型的角度來講,它們與線性表又有著巨大的不同。本節將介紹雙端隊列的定義及其不同實現,並給出雙端隊列的一些實際應用。
透過本節學習,應掌握以下內容:
雙端佇列(double-end queue, deque) 也是插入和刪除操作分別被限制在序列兩端的線性表,但與堆疊和佇列不同的是,雙端隊列的限制很少,對於雙端隊列而言,隊尾(rear) 和隊頭(front) 均允許插入元素和刪除元素。新元素既可以被加到隊頭, 也可以被加到隊尾。同理,已有的元素也能從任何一端移除。某種意義上,可以認為雙端隊列是棧和隊列的結合。
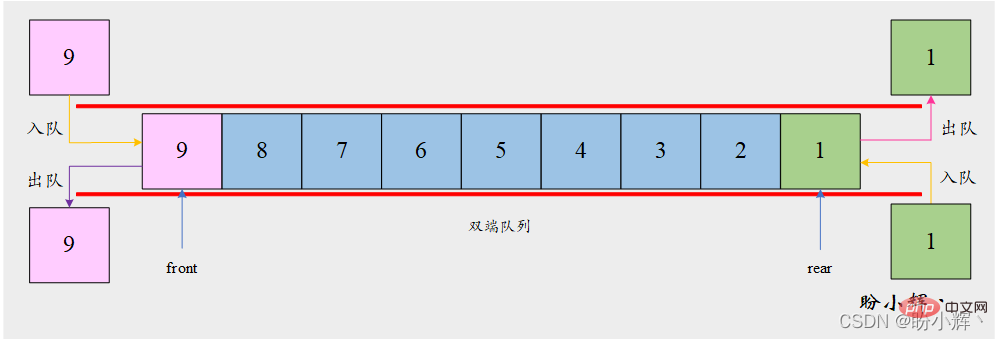
儘管雙端佇列有堆疊和佇列的許多特性,但是它並沒有要求按照這兩個資料結構所限定的LIFO 原則和FIFO 原則操作元素。
除了新增和移除元素外,雙端佇列還具有初始化、判隊空和求隊長度等輔助操作。具體而言,雙端佇列的抽象資料型別定義如下:
2. 雙端隊列的實現和普通隊列一樣,雙端隊列同樣有順序存儲和鍊式儲存兩種儲存表示方式。基本操作:
刪除並返回隊尾元素
1. __itit__(): 初始化雙端佇列
建立一個空雙端佇列
2. size(): 求取並傳回雙端佇列中所含元素的個數n
若雙端佇列為空,則傳回整數0
3.isempty(): 判斷是否為空雙端 0
3.端佇列
判斷雙端佇列中是否儲存元素
4. addfront(data): 雙端佇列中是否儲存元素
將元素data 插入隊頭
5. addrear(data):## 5. addrear(data):##2端隊列隊尾新增元素
將元素data 插入隊尾
6. removefront(): 刪除雙端隊列隊頭元素
刪除並返回隊頭元素
7. removerear(雙端隊列隊尾元素
類似於順序佇列,雙端佇列的順序儲存結構利用一組位址連續的儲存單元依序存放從雙端隊列頭到雙端隊列尾的元素,同時需要用兩個指標front 和rear 分別指示隊列頭元素和隊列尾元素的位置。初始化空雙端隊列時,front=rear=0,當元素入隊時,rear 加1,而元素出隊時,front 加1
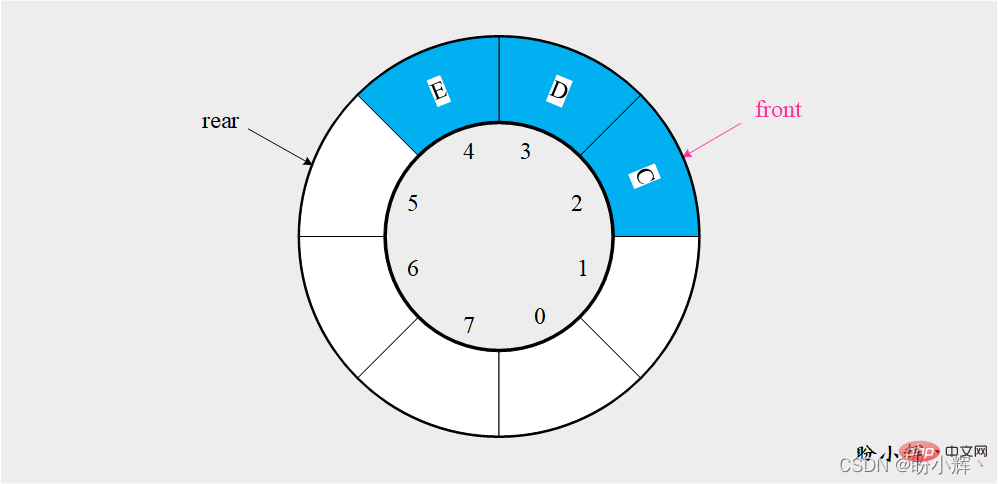
順序雙端佇列的初始化需要4 部分資訊:deque 清單用於儲存資料元素,max_size 用於儲存queue 清單的最大長度,以及front 和rear
class Deque: def __init__(self, max_size=6): self.max_size = max_size self.deque = [None] * self.max_size self.front = 0 self.rear = 0
由於front 和rear 分別用於記錄隊頭元素和隊尾元素的索引,因此我們可以方便的計算出雙端隊列的長度;同時我們需要考慮雙端隊列為循環隊列,front 可能大於rear,不能直接通過rear-front,我們需要利用公式計算解決此問題:
Python 實作如下:
def size(self): return (self.rear-self.front+self.max_size) % self.max_size
根據front 和rear 的值可以方便的判斷雙端隊列是否為空:
def isempty(self): return self.rear==self.front
根據front 和rear 的值可以方便的判斷雙端隊列是否還有剩餘空間:
def isfull(self): return ((self.rear+1) % self.max_size == self.front)
新增元素時,需要先判斷雙端佇列中是否還有空閒空間,然後根據雙端佇列為定長順序雙端佇列或動態順序雙端佇列,新增元素操作稍有不同:
[定長順序雙端佇列的新增元素操作] 若隊滿,則引發例外:
# 注意队头和队尾修改索引的添加元素的不同顺序
def addrear(self, data):
if not self.isfull():
self.deque[self.rear] = data
self.rear = (self.rear+1) % self.max_size else:
raise IndexError("Full Deque Exception")
def addfront(self, data):
if self.isfull():
self.resize()
if self.isempty():
# 当Python資料結構與演算法學習之雙端佇列
self.deque[self.rear] = data
self.rear = (self.rear+1) % self.max_size else:
self.front = (self.front - 1 + self.max_size) % self.max_size
self.deque[self.front] = data[動態順序雙端佇列的新增元素操作] 如果雙端佇列滿,則先申請新空間,然後再執行新增動作:
def resize(self): new_size = 2 * self.max_size new_deque = [None] * new_size d = new_size - self.max_size for i in range(self.max_size): new_deque[(self.front+i+d) % new_size] = self.deque[(self.front+i) % self.max_size] self.deque = new_deque self.front = (self.front+d) % new_size self.max_size = new_size # 注意队头和队尾修改索引的添加元素的不同顺序 def addrear(self, data): if self.isfull(): self.resize() self.deque[self.rear] = data self.rear = (self.rear+1) % self.max_size def addfront(self, data): if self.isfull(): self.resize() self.front = (self.front - 1 + self.max_size) % self.max_size self.deque[self.front] = data
與動態順序佇列類似,我們同樣需要考慮複製之後的索引,否則可能出現存在不能用的空閒空間:
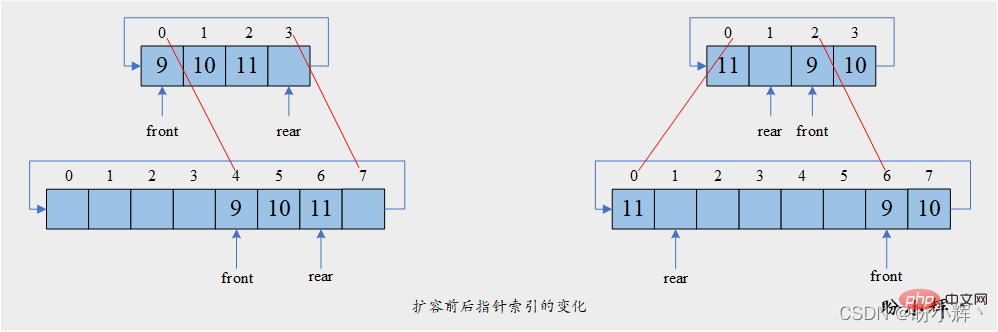
新增元素的時間複雜度為 O(1)##。雖然當動態順序雙端佇列滿時,原始雙端佇列中的元素需要先複製到新雙端佇列中,然後新增元素,但參考《順序表及其操作實作》中順序表追加操作的介紹,由於n 次加入元素運算的總時間T##(##n #) 與#O(n) 成正比,因此其攤銷時間複雜度可以認為O(1)。 2.1.6 刪除隊頭或隊尾的元素
# 注意队头和队尾修改索引的删除元素的不同顺序
def removefront(self):
if not self.isempty():
result = self.deque[self.front]
self.front = (self.front+1) % self.max_size return result else:
raise IndexError("Empty Deque Exception")
def removerear(self):
if not self.isempty():
self.rear = (self.rear - 1 + self.max_size) % self.max_size
result = self.deque[self.rear]
return result else:
raise IndexError("Empty Deque Exception")2.2 鏈雙端佇列的實作
addrear 操作分別是透過在鍊錶頭部和尾部插入元素來實現的,而removefront 操作和removerear 操作分別是透過從頭部和尾部刪除結點來實現的。為了降低在尾端刪除結點的時間複雜度,接下來基於雙向鍊錶實作雙端佇列。
2.2.1 雙端佇列結點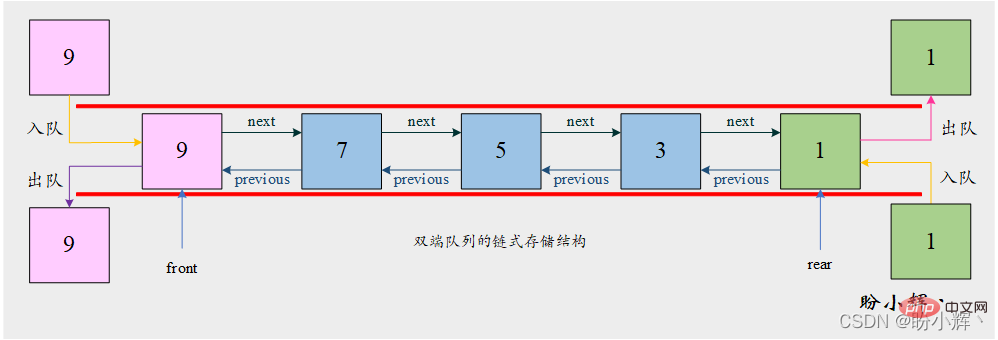
class Node: def __init__(self, data=None): self.data = data self.next = None def __str__(self): return str(self.data)
rear 都指向 None,並初始化雙端佇列長度:
class Deque: def __init__(self): self.front = None self.rear = None self.num = 0
2.2.3 求雙端佇列長度傳回num 屬性,則需要遍歷整個鍊錶才能得到雙端佇列長度:
def size(self): return self.num
2.2.4 判雙端佇列空根據雙端隊列的長度可以很容易的判斷其是否為空雙端隊列:def isempty(self): return self.num
front 指針,並且同時也要修改結點的next 和previous 指標;如果加入元素前雙端佇列為空,還需要進行對應處理:
def addrear(self, data): node = Node(data) # 如果添加元素前Python資料結構與演算法學習之雙端佇列为空,则添加结点时,需要将front指针也指向该结点 if self.front is None: self.rear = node self.front = node else: node.previous = self.rear self.rear.next = node self.rear = node self.num += 1 def addfront(self, data): node = Node(data) # 如果添加元素前Python資料結構與演算法學習之雙端佇列为空,则添加结点时,需要将rear指针也指向该结点 if self.rear is None: self.front = node self.rear = node else: node.next = self.front self.front.previous = node self.front = node self.num += 1
若Python資料結構與演算法學習之雙端佇列不空,可以从删除队头或队尾元素并返回,删除操作需要更新队头指针 front 以及尾指针 rear,同时也要修改结点的 next 和 previous 指针,若出队元素尾队中最后一个结点,还需要进行相应处理:
def removefront(self):
if self.isempty():
raise IndexError("Empty Queue Exception")
result = self.front.data
self.front = self.front.next
self.num -= 1
if self.isempty():
self.rear = self.front else:
# 若删除操作完成后,Python資料結構與演算法學習之雙端佇列不为空,将 front 指针的前驱指针指向 None
self.front.previous = None
return result
def removerear(self):
if self.isempty():
raise IndexError("Empty Queue Exception")
result = self.rear.data
self.rear = self.rear.previous
self.num -= 1
if self.isempty():
self.front = self.rear else:
# 若删除操作完成后,Python資料結構與演算法學習之雙端佇列不为空,将 rear 指针的后继指针指向 None
self.rear.next = None
return resultPython資料結構與演算法學習之雙端佇列的不同实现对比与栈的不同实现类似,可以参考《栈及其操作实现》。
接下来,我们首先测试上述实现的Python資料結構與演算法學習之雙端佇列,以验证操作的有效性,然后利用实现的基本操作来解决实际算法问题。
首先初始化一个顺序Python資料結構與演算法學習之雙端佇列 deque,然后测试相关操作:
# 初始化一个最大长度为5的Python資料結構與演算法學習之雙端佇列dq = Deque(5)print('Python資料結構與演算法學習之雙端佇列空?', dq.isempty())for i in range(3):
print('队头添加元素:', 2*i)
dq.addfront(2*i)
print('队尾添加元素:', 2*i+1)
dq.addrear(2*i+1)print('Python資料結構與演算法學習之雙端佇列长度为:', dq.size())for i in range(3):
print('队尾删除元素:', dq.removerear())
print('队头删除元素:', dq.removefront())print('Python資料結構與演算法學習之雙端佇列长度为:', dq.size())测试程序输出结果如下:
Python資料結構與演算法學習之雙端佇列空? True队头添加元素: 0队尾添加元素: 1队头添加元素: 2队尾添加元素: 3队头添加元素: 4队尾添加元素: 5Python資料結構與演算法學習之雙端佇列长度为: 6队尾删除元素: 5队头删除元素: 4队尾删除元素: 3队头删除元素: 2队尾删除元素: 1队头删除元素: 0Python資料結構與演算法學習之雙端佇列长度为: 0
首先初始化一个链Python資料結構與演算法學習之雙端佇列 queue,然后测试相关操作:
# 初始化新队列dq = Deque()print('Python資料結構與演算法學習之雙端佇列空?', dq.isempty())for i in range(3):
print('队头添加元素:', i)
dq.addfront(2*i)
print('队尾添加元素:', i+3)
dq.addrear(2*i+1)print('Python資料結構與演算法學習之雙端佇列长度为:', dq.size())for i in range(3):
print('队尾删除元素:', dq.removerear())
print('队头删除元素:', dq.removefront())print('Python資料結構與演算法學習之雙端佇列长度为:', dq.size())测试程序输出结果如下:
Python資料結構與演算法學習之雙端佇列空? True队头添加元素: 0队尾添加元素: 3队头添加元素: 1队尾添加元素: 4队头添加元素: 2队尾添加元素: 5Python資料結構與演算法學習之雙端佇列长度为: 6队尾删除元素: 5队头删除元素: 4队尾删除元素: 3队头删除元素: 2队尾删除元素: 1队头删除元素: 0Python資料結構與演算法學習之雙端佇列长度为: 0
[1] 给定一字符串 string (如:abamaba),检查其是否为回文。
使用Python資料結構與演算法學習之雙端佇列可以快速检查一字符串是否为回文序列,只需要将字符串中字符依次入队,然后从Python資料結構與演算法學習之雙端佇列两端依次弹出元素,对比它们是否相等:
def ispalindrome(string): deque = Deque() for ch in string: deque.addfront(ch) flag = True while deque.size() > 1 and flag: ch1 = deque.removefront() ch2 = deque.removerear() if ch1 != ch2: flag = False return flag
验证算法有效性:
print('abcba是否为回文序列:', ispalindrome('abcba'))print('charaahc是否为回文序列:', ispalindrome('charaahc'))结果输出如下:
abcba是否为回文序列: True charaahc是否为回文序列: False
推荐学习:python教程
以上是Python資料結構與演算法學習之雙端佇列的詳細內容。更多資訊請關注PHP中文網其他相關文章!


