線性時間選擇-常見問題-PHP中文網

線性時間選擇

定義：給定線性序集中n個元素和一個整數k，1≤k≤n，要求找出這n個元素中第k小的元素。

（1）在某些特殊情況下，很容易設計出解選擇問題的線性時間演算法。如：當要選擇最大元素或最小元素時，顯然可以在O(n)時間完成。（一趟比較即可）

（2）一般的選擇問題，特別是中位數的選擇問題似乎比最小（大）元素要難。但實際上，從漸近階的意義上，它們是一樣的。也可以在O(n)時間完成。

線性時間選擇方法一：randomizedSelect

想法：改編隨機快速排序，不用把整個陣列全部排序，而是選擇的排序（更快）

時間複雜度：

（1）在最壞情況下，演算法randomizedSelect需要O(n^2)計算時間

eg.要找最小的元素，但是每次進行Partition函數劃分時得到的位置總是很大（靠近n）（即總是在最大元素出劃分）

（2）但可以證明，演算法randomizedSelect可以在O(n)平均時間內找出n個輸入元素中的第k小元素。

程式碼如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

int Partition(int a[],int p,int r){
    int i=p,j=r+1,x=a[p];
    while(1){
        while(a[++i]<x&&i<r);
        while(a[--j]>x);
        if(i>=j)break;
        swap(a[i],a[j]);
    }
    a[p]=a[j];
    a[j]=x;
    return j;
}

int RandomizedPartition(int a[],int p,int r){
    int i=rand()%(r-p)+p;
    swap(a[p],a[i]);
    return Partition(a,p,r);
}

int RandomizedSelect(int a[],int p,int r,int k){
    if(p==r)return a[p];
    int i=RandomizedPartition(a,p,r);//返回基准元素的位置
    int j=i-p+1;//表示基准元素及其左边一共多少个元素
    if(k<=j)RandomizedSelect(a,p,i,k);
    else RandomizedSelect(a,i+1,r,k-j);
}
int main(){
    int a[10]={3,1,7,6,5,9,8,2,0,4};
    int x;
    while(scanf("%d",&x)!=EOF){
        int ans=RandomizedSelect(a,0,9,x);
        printf("%d\n",ans);
    }
}

登入後複製

線性時間選擇方法二：

如果能在線性時間內找到一個分割基準，使得依這個基準所分割出的2個子數組的長度都至少為原數組長度的ε倍(0<ε<1是某個正常數)，那麼就可以在最壞情況下用O(n)時間完成選擇任務。

例如，若ε=9/10，演算法遞歸呼叫所產生的子數組的長度至少縮短1/10。所以，在最壞情況下，演算法所需的計算時間T(n)滿足遞歸式T(n)≤T(9n/10) O(n) 。由此可得T(n)=O(n)。

老師講這時，我記得很清，強調了找到而非確定，「找到」是找到我們想要得中位數的值，而我們之前的快排等都是確定值的位置，也就是把基準元素放到正確的位置上。

步驟：

#（1）將n個輸入元素分割成n/5（向上取整）個組，每組5個元素，最多只可能有一個組不是5個元素。用任一排序演算法，將每組中的元素排好序，並取出每組的中位數，共n/5（向上取整）個。

（2）遞迴呼叫select來找出這n/5（向上取整）個元素的中位數。如果n/5（向上取整）是偶數，就找它的2個中位數中較大的一個。以這個元素作為劃分基準。

分割策略示意圖：

白色圓點：每組的中位數；點x：中位數的中位數

線性時間選擇

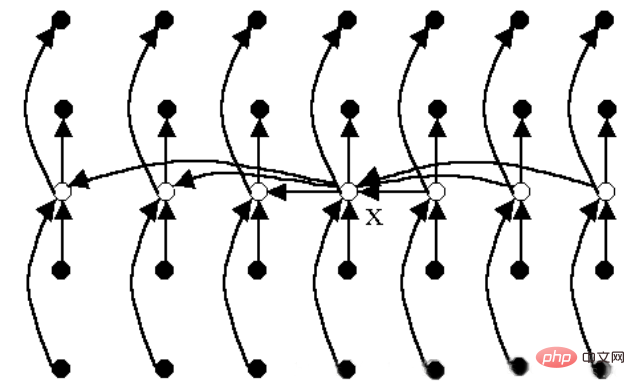
範例：

依遞增順序，找出下面29個元素的第18個元素：8,31,60,33,17,4,51,57,49,35,11,43,37,3,13,52,6,19,25,32,
54,16,5,41,7,23,22,46,29.
(1) 將前面25個元素分成5(=floor(29/5))組: (8,31,60, 33,17),(4,51,57,49,35),(11,43,37,3,13),(52,6,19,25,32),(54,16,5,41, 7);
(2) 提取每一組的中位數元素，構成集合{31,49,13,25,16}；
(3) 遞歸地使用演算法求取該集合的中位數，得到m=25；
(4) 根據m=25, 把29個元素分成3個子數組（按原有順序）
P={8,17,4,11, 3,13,6 ,19,16,5,7,23,22}
Q={25}

R={31,60,33,51,57,49,35,43,37,52, 32,54,41,46,29}

(5) 由於|P|=13,|Q|=1,k=18，所以放棄P,Q，使k=18-13-1 =4，對R遞歸地執行本演算法；
(6) 將R劃分成3(floor(15/5))組：{31,60,33,51,57},{49,35,43 ,37,52},{32,54,41,46,29}
(7) 求這3組元素的中位數元素分別為：{51,43,41}，此集合的中位數元素是43;
(8) 依43將R分成3組：

{31, 33, 35,37,32, 41, 29},{43},{60, 51,57 , 49, 52,54, 46}

複雜度：

設數組長度為n
當n<75時，演算法select所用的計算時間不超過某一常數C1
當n≥75時，for迴圈執行n/5次，每次用時為某一常數（固定個數即5個中查找！）；select找中位數的中位數數，由於長度為原長度的1/5，所以用時可記為T(n/5)；劃分以後所得到數組至多有3n/4個元素，用時記為T(3n/4)。所以T(n)可以遞歸表示為：

線性時間選擇

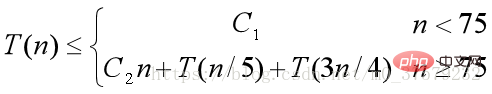
解此遞歸式為T(n)=O(n)

上述算法将每一组的大小定为5，并选取75作为是否作递归调用的分界点（大于75使用该算法）。这2点保证了T(n)的递归式中2个自变量之和n/5+3n/4=19n/20=εn，0<ε<1。这是使T(n)=O(n)的关键之处。当然，除了5和75之外，还有其他选择。

注意：

（1）设中位数的中位数是x，比x小和比x大的元素至少3*(n-5)/10个，原因：

3*(n/5-1)*1/2

3---中位数比x小的每一组中有3个元素比x小

n/5-1---有5个数的组数

1/2---大概有1/2组的中位数比x小

（2）而当n≥75时，3(n-5)/10≥n/4所以按此基准划分所得的2个子数组的长度都至少缩短1/4，也就是说，长度最长为原长度的3/4。

線性時間選擇

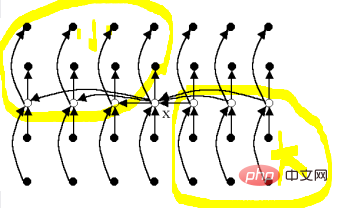
如图，划分的部分左上是肯定比x小的（大概占1/4）右下是肯定比x大的（大概占1/4）左下和右上不确定，就算这两部分同时不比x小或比x大，划分成的子区间也能至少缩短1/4!

核心代码：

Type Select(Type a[], int p, int r, int k)
{
      if (r-p<75) {
        //用某个简单排序算法对数组a[p:r]排序;
        return a[p+k-1];
        };
      for (int i=0;i<=(r-p-4)/5;i++)//i即为n个元素的分组个数
      //将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
      //将中位数元素换至前面
  
      //找中位数的中位数，r-p-4即上面所说的n-5
      Type x=Select(a,p,p+(r-p-4)/5,(r-p-4)/10);//x是中位数的中位数
      int i=Partition(a,p,r,x),j=i-p+1;//i为快排一趟找到区间[p,r]中x应该在的位置，j为[p,i]区间的元素个数
      if (k<=j) return Select(a,p,i,k);
      else return Select(a,i+1,r,k-j);
}

登入後複製

关键的代码是：

for ( int i = 0; i<=(r-p-4)/5; i++ )//i即为n个元素的分组个数
      //将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
      //将中位数元素换至前面

登入後複製

一共(r-p+1)/5个组

注意这里i从0开始表示，为了方便交换时带入数组的下标，0-(r-p-4)/5，即一共(r-p-4)/5+1各组，即(r-p+1)/5个组

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<stack>
#include<algorithm>
using namespace std;

void bubbleSort(int a[],int p,int r){
    for(int i=p;i<r;i++){
        for(int j=i+1;j<=r;j++){
            if(a[j]<a[i])swap(a[i],a[j]);
        }
    }
}

int Partition(int a[],int p,int r,int val){
    int pos;
    for(int q=p;q<=r;q++){
        if(a[q]==val){pos=q;break;}
    }
    swap(a[p],a[pos]);

    int i=p,j=r+1,x=a[p];
    while(1){
        while(a[++i]<x&&i<r);
        while(a[--j]>x);
        if(i>=j)break;
        swap(a[i],a[j]);
    }
    a[p]=a[j];
    a[j]=x;
    return j;
}

int Select(int a[],int p,int r,int k){
    if(r-p<75){
        bubbleSort(a,p,r);
        return a[p+k-1];
    }

    for(int i=0;i<=(r-p-4)/5;i++){//把每个组的中位数交换到区间[p,p+(r-p-4)/4]
        int s=p+5*i,t=s+4;
        for(int j=0;j<3;j++){//冒泡排序，从后开始排，结果使得后三个数是排好顺序的（递增）
            for(int n=s;n<t-j;n++){
                if(a[n]>a[n+1])swap(a[n],a[n-1]);
            }
        }
        swap(a[p+i],a[s+2]);//交换每组中的中位数到前面
    }
    //(r-p-4)/5表示组数-1，则[p,p+(r-p-4)/5]的区间长度等于组数
    int x=Select(a,p,p+(r-p-4)/5,(r-p-4)/10);//求中位数的中位数
    int i=Partition(a,p,r,x),j=i-p+1;
    if(k<=j)return Select(a,p,i,k);
    else return Select(a,i+1,r,k-j);
}
int main(){
    int x;
    //数组a存了0-79
    int a[80]={3,1,7,6,5,9,8,2,0,4,
               13,11,17,16,15,19,18,12,10,14,
               23,21,27,26,25,29,28,22,20,24,
               33,31,37,36,35,39,38,32,30,34,
               43,41,47,46,45,49,48,42,40,44,
               53,51,57,56,55,59,58,52,50,54,
               63,61,67,66,65,69,68,62,60,64,
               73,71,77,76,75,79,78,72,70,74,
              };
    while(scanf("%d",&x)!=EOF){
        printf("第%d大的数是%d\n",x,Select(a,0,79,x));
    }
}

登入後複製

qwq，博主nc写错输出了，“第i小的数”

線性時間選擇