用C++實作最短路徑之Dijkstra演算法-C#.Net教程-PHP中文網

用C++實作最短路徑之Dijkstra演算法

little bottle

發布： 2019-04-09 10:53:52

轉載

7647 人瀏覽過

網路層的連結狀態路由選擇演算法（LS演算法），其中一種就是用Dijkstra演算法寫的。《演算法導論》的介紹：Dijkstra演算法解決的是帶有權重的有向圖上單源最短路徑問題，該演算法要求所有邊的權重都為非負值。

演算法思路

G集表示所有點集，S集表示已經求解出來源到某點的最短路徑的點集，V集表示為求出最短路徑的點集
首先令S=Ø，V=G

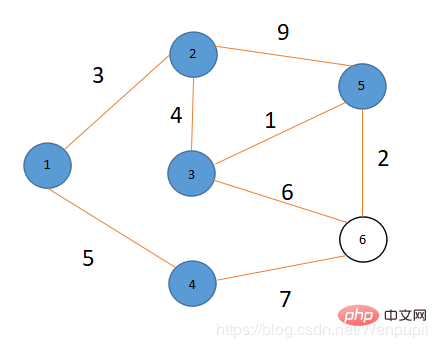
如圖所示6個點8條邊 V={ 1,2,3,4,5,6}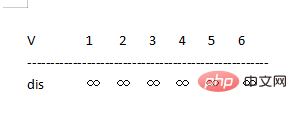
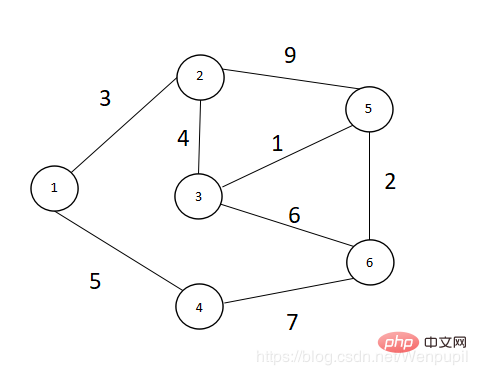
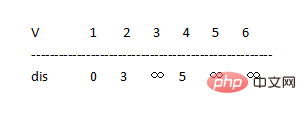
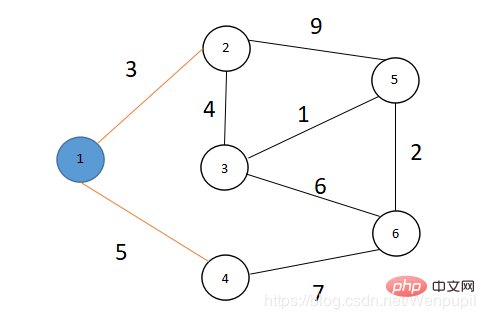
用C++實作最短路徑之Dijkstra演算法

#取u=1，把點1放入S中，S={1} ,V ={2,3,4,5,6}，遍歷與點1相連的點，並把權值放入數組

4.由路徑數組可得知此時V集中點2有最短路徑（值為3）所以令u=2，則S={1,2} ,V={3,4,5,6}

因為dis[3]=dis[2] 4 ⇒ 7=3 4
… . dis[5]=dis[2] 9 ⇒ 12=3 9
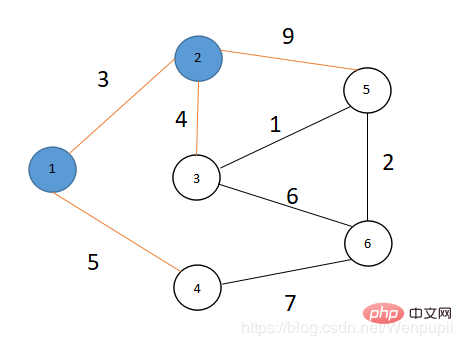
用C++實作最短路徑之Dijkstra演算法

同理如今S={1,2},V={3,4,5,6},在V中發現dis[3]為除dis[1],dis[2]以外的最小值，所以令S=S∪{3}
此時S={1,2,3},V={4,5,6}

dis[5]=12>dis[3] 1=7 1 ⇒ 令dis[5]=dis[3] 1=7 1=8
因為dis[6]=∞ >dis[3] 6= 7 6 ⇒ 令dis[6]=dis[6] 6=7 6=13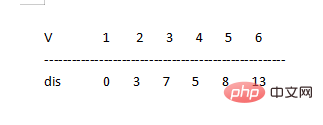
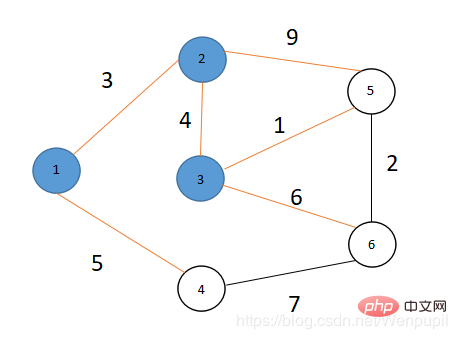
用C++實作最短路徑之Dijkstra演算法

同理如今S={1,2,3}, V={4,5,6},在V中發現dis[4]為除dis[1],dis[2],dis[3]外的最小值，所以令S=S∪{4}
此時S={1,2,3,4},V={5,6}

#因為dis[6]=13>dis[4] 7 =5 7 ⇒ 令dis[6]=dis[4] 7=5 7=12
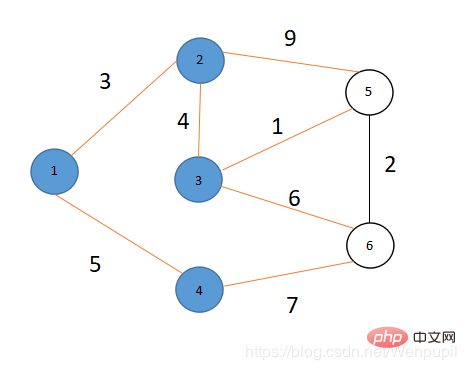
用C++實作最短路徑之Dijkstra演算法

同理如今S={1,2,3, 4},V={5,6},在V中發現dis[5]為除dis[1],dis[2],dis[3],dis[4]外的最小值，所以令S=S ∪{5}
此時S={1,2,3,4,5},V={6}

因為dis[6]=12> ;dis[5] 2=8 2 ⇒ 令dis[6]=dis[5] 2=8 2=10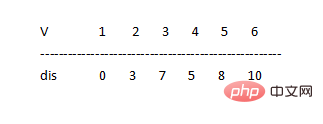
用C++實作最短路徑之Dijkstra演算法

如上從點1到各點的最短路徑就求出來，感覺最近寫的很亂，不容易看懂。不過感謝各位看官能夠看到這兒。
關於n點m條邊求最短路徑，一般迭代n次就能得到所有點的最短路徑。
現在就是貼出程式碼惹

/*
 * @author Wenpupil
 * @time  2019-04-04
 * @version 1.0
 * @Description 最短路径之Dijkstra算法 关于无负权的无向图练习 
 */
#include<iostream>
#include<cmath>
#include<string.h>
#define INIT  9999
using namespace std;
int map[20][20];              //存储19个点的无向图
int s[20];                    //标记数组 
int dis[20];

void mDijkstra(int i,int m)
{
	for(int i=0;i0){
				dis[j]=min(dis[j],dis[u]+map[u][j]);
			}
		}
	}
}

int main(void)
{
	int m,n;                     //共有m个点，n条边
	cin>>m>>n;
	for(int i=0;i<n int cin>>x>>y>>z;
		map[x][y]=map[y][x]=z;
	}
	mDijkstra(1,m);             //从节点1出发 遍历全图
	
	for(int i=1;i<link href="https://csdnimg.cn/release/phoenix/mdeditor/markdown_views-258a4616f7.css" rel="stylesheet">
<!-- flowchart 箭头图标 勿删 --><svg xmlns="http://www.w3.org/2000/svg" style="display: none;"><path stroke-linecap="round" d="M5,0 0,2.5 5,5z" id="raphael-marker-block" style="-webkit-tap-highlight-color: rgba(0, 0, 0, 0);"></path></svg><h2>
<span style="font-size: 16px;">【推薦課程：</span><a href="//m.sbmmt.com/course/list/38.html" target="_self" style="font-size: 16px; text-decoration: underline;"><span style="font-size: 16px;"># C 影片教學</span></a><span style="font-size: 16px;">】</span>
</h2></n></string.h></cmath></iostream>

登入後複製

以上是用C++實作最短路徑之Dijkstra演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章！