這次帶給大家前端中排序演算法實例詳解,前端中排序演算法使用的注意事項有哪些,下面就是實戰案例,一起來看一下。
前天看到知乎上有一篇文章在吐槽阮一峰老師的快速排序算法,這裡插一句題外話,我覺得人非聖賢孰能無過,盡信書不如無書,學習的過程也就是不斷發現錯誤改正錯誤的過程,有人幫我們糾正了這個錯誤我們應該開心,但是我覺得不應該批判阮一峰老師,他也在不斷地學習,不斷地糾錯成長,所以大家都一樣,無所謂誤導,如果出錯的不是他,是更厲害的牛人呢?JavaScript的作者呢?所以大家都會出錯,我們也應該多思考,抱著懷疑的態度接納,時刻思考這是不是最優的解法,還有沒有更好的呢,我想這才是我們應該做的.
而我,作為一個計算機專業的前端,卻不能很好地實現各種思想的排序演算法,我覺得很慚愧,所以我就抽時間仔細查看了C語言描述中文版.pdf>>這本書,下面我就對我理解的各種思想的排序算法做一下總結,希望可以給大家一些參考和收穫,如有不妥之處,煩請指出,也可以分享你們覺得更好地想法,我覺得大家一起學習一起進步是最快樂的事~
(1) 時間複雜度的概念
演算法的時間複雜度是一個函數,他定性地描述了某個演算法的運行時間,常用大O符號,不包括這個函數的低階項和高階項係數.
(2) 計算方法
一般情況下,演算法中基本運算的執行次數是問題規模n的某個函數,用T(n)表示,若有某個輔助函數f(n),使得當n趨近於無窮大時,T(n)/f(n)的極限值為不為零的常數,則f(n)是T(n)的同數量級函數,記作T(n) = O(f( n)),稱O(f(n))為演算法的漸進時間複雜度,簡稱為時間複雜度.
分析: 隨時模組n的增大,演算法的執行時間的成長率和f(n)的成長率成正比,所以f(n)越小,演算法的時間複雜度越低,演算法的效率越高.
在計算時間複雜度的時候,先找出演算法的基本運算,然後計算出基本運算的執行次數,找出T(n)的同數量級f(n)(它的同數量級一般有以下: 1, log₂n, n,nlog₂n,n的平方,n的三次方),若T(n) / f(n)求極限得到一常數c,則時間複雜度T(n) = O(f(n)):
舉例如下:
for(i = 1; i<p style="text-align: left;">我們可以得到T(n) = n^3 n^2,我們可以確定n^3為T(n)的同數量級, f(n)=n^3;則T(n) / f(n) = 1 1/n 求極限為常數1,所以該演算法的時間複雜度為:<br> T(n) = O(n ^3);</p><p style="text-align: left;"><strong>說明: 為了方便我接下來都是使用N來代指數組元素個數的.</strong></p><h1 style="text-align: left;">2. 排序演算法</h1><h2 style="text-align: left;">#2.1 <a href="//m.sbmmt.com/code/12106.html" target="_blank">冒泡排序</a>
</h2><h3 style="text-align: left;">2.1.1 主要思想:</h3><p style="text-align: left;">冒泡排序的主要思想就是對一個長度為n的數組進行遍歷, i從n -1到1的,數組的前i個元素的最大值放在i位置上,假想冒泡排序是一個豎著的水柱,遍歷的過程就是,大的值(重的)不斷沉下來,小的值(輕的)不斷浮上去,這樣遍歷結束後,每個位置上的值都比他前面的值大,排序結束.</p><h3 style="text-align: left;">2.1.2 時間複雜度</h3><p style="text-align: left;">最壞情況下的時間複雜度: o(n^2);<br>最好情況下的時間複雜度: o(n^2);</p><h3 style="text-align: left;">2.1.3 排序過程圖解:</h3> <p style="text-align: left;"><strong>圖解中的出循環是退出內層循環</strong><br><img src="https://img.php.cn/upload/article/000/061/021/975255cd4031086ad718d4dc21df07d0-0.png" alt="前端中排序演算法實例詳解" title="前端中排序演算法實例詳解"></p><h3 style="max-width:90%">2.1.4 代码实现:</h3><h4 style="text-align: left;">冒泡排序-非递归实现</h4><pre class="brush:php;toolbar:false">function bubbleSort(arr) {
for(var i = arr.length - 1; i > 1; i--) {
for(var j=0; j arr[j+1]) {
var temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
return arr;
}
var arr = [34,8,64,51,32,21];
bubbleSort(arr); // [8, 21, 32, 34, 51, 64]function bubbleSort(arr, n) {
if(n arr[j+1]) {
var temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
return bubbleSort(arr, --n);
}
}
var arr = [34,8,64,51,32,21];
bubbleSort(arr, arr.length); // [8, 21, 32, 34, 51, 64]插入排序有 n-1 趟排序组成,对于 i=1 到 i=n-1 趟,内层循环j从 i 到 1, 如果这其中有 j-1 位置上的元素大于 i 位置上的元素,就将该元素后移,知道条件不成立退出循环,这个时候大的值都被移动到后面了,j这个位置就是i位置上的元素应该在的位置.这样保证了每次循环i位置前的所有元素都是排好序的,新的循环就只需要 将 i 位置上的元素 和 j-1(也就是初始的 i-1) 位置上的元素作比较,如果大于则无需再往前比较,如果小于则继续往前比较后移.
最坏情况下的时间复杂度: o(n^2);
最好情况下的时间复杂度: o(n);
图解中的出循环是退出内层循环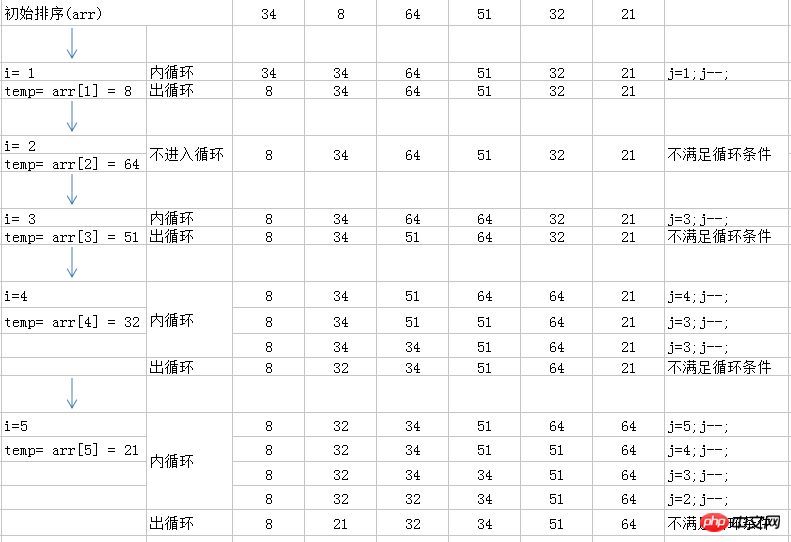
function insertSort(arr) {
var n = arr.length,temp = 0;
for(var i = 1; i 0 && arr[j-1] > temp; j--) {
arr[j] = arr[j - 1];
}
arr[j] = temp;
}
return arr;
}
var arr = [34,8,64,51,32,21];
insertSort(arr); // [8, 21, 32, 34, 51, 64]function insertSort(arr, n) {
if(n > 0 && n 0 && arr[j - 1] > temp) {
arr[j] = arr[j - 1];
j--;
}
arr[j] = temp;
i++;
return insertSort(arr, i);
}
return arr;
}
var arr = [34,8,64,51,32,21];
insertSort(arr, 1); // [8, 21, 32, 34, 51, 64]; // 这个函数的调用限定了第一次调用n的值只能传1顾名思义,快速排序是在实践中最快的已知排序算法,它的平均运行时间是O(Nlog₂N).快速排序的关键在于枢纽元的选取,有一种比较推荐的选取方法就是选取左端的值,右端的值,中间位置的值(L(left + right) / 2)这三个数的中位数.举例: 输入为8,1,4,9,6,3,5,2,7,0, 左边元素8, 右边元素0,中间位置上的元素L(0+9)/2是4位置上的元素是6,L在表示向下取整.
8,0,6的中位数,先排序0,6,8, 这三个数的中位数是6.
通过一趟排序将要排序的部分分割成独立的两部分,其中一部分数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据进行快速排序,整个排序过程可以递归进行,依次达到整个数据变成有序序列.
第一步: 设置两个变量i,j,排序开始的时候: i=left,j=right-1,left和right分别表示要进行快速排序序列的起始索引和结束索引;
第二步: 从数组中随机选取一个元素,将其与arr[left]进行交换,即privot = arr[left],保证每一次的基准值都在序列的最左边;
第三步: 由j开始向前搜索,即由后开始向前搜索(j--),找到第一个小于privot 的值arr[j],将arr[i]与arr[j]互换;
第四步: 从i开始向后搜索,即由前开始向后搜索(i++),找到一个大于privot 的arr[i],将arr[i]与arr[j]互换;
第五步: 重复第三步和第四步,直到不满足i
平均情况下的时间复杂度: o(nlog₂n);
最好情况下的时间复杂度: o(n);

function quickSort(arr, left, right) {
if(left >= right) return;
var i = left;
var j = right - 1;
var privot = arr[left];
//console.log(privot);
while(i = privot) j--;
arr[i] = arr[j];
while(i<j var quicksort><h4 style="text-align: left;">快速排序-非递归实现</h4>
<pre class="brush:php;toolbar:false">function mainProduce(arr, left, right) {
var i = left, j = right - 1;
var rendomIndex = Math.floor(Math.random() * (j - i)) + left;
var temp = arr[left];arr[left] = arr[rendomIndex];arr[rendomIndex] = temp;
var privot = arr[left];
while(i = privot) j--;
var temp = arr[i];arr[i] = arr[j];arr[j] = temp;
while(i<j> left + 1) {
s.push(left);s.push(mid);
}
if(mid left + 1) {
s.push(left);s.push(mid);
}
if(mid <h2 style="text-align: left;">2.4 希尔排序</h2>
<h3 style="text-align: left;">2.4.1 主要思想</h3>
<p style="text-align: left;">希尔排序是把记录按照下标的一定增量分组,对每组使用插入排序;随着增量逐渐减少,分割的数组越来越大,当增量减至1,整个<a href="//m.sbmmt.com/code/54.html" target="_blank">数组排序</a>完成,算法终止.</p>
<h3 style="text-align: left;">2.4.2主要步骤</h3>
<p style="text-align: left;">第一步: 选取一个增量d,初始值是Math.floor(len/2);<br>第二步: 然后将数组中间隔为增量d的组成新的分组,然后对这个分组的元素排序,完成排序后,增量除以2得到新的增量;<br>第三步: 重复第二步,直到增量为1,间隔为1的元素组成的分组就是整个数组,然后再对整个数组进行插入排序,得到最后排序后数组.</p>
<p style="text-align: left;">希尔排序是不稳定的,它在不断地交换的过程中会改变原来相等的元素的顺序.</p>
<h3 style="text-align: left;">2.4.3 时间复杂度</h3>
<p style="text-align: left;">平均情况下的时间复杂度: o(nlog₂n);<br>最好情况下的时间复杂度: o(n);</p>
<h3 style="text-align: left;">2.4.4 前端中排序演算法實例詳解</h3>
<p style="text-align: left;"><img src="https://img.php.cn/upload/article/000/061/021/2f13ca0ab50333d1dad5851595e7225d-3.jpg" alt="前端中排序演算法實例詳解" title="前端中排序演算法實例詳解"></p>
<p style="text-align: left;">图片源于自百度百科: 图片来源</p>
<h3 style="text-align: left;">2.4.5 代码实现:</h3>
<h4 style="text-align: left;">希尔排序-递归实现</h4>
<pre class="brush:php;toolbar:false">function shellSort(arr, increment) {
var len = arr.length;
if(increment > 0) {
for(var i = increment; i = 0 && arr[j] > arr[j + increment]; j -= increment) {
var temp = arr[j];
arr[j] = arr[j + increment];
arr[j + increment] = temp;
}
}
return shellSort(arr, Math.floor(increment/2));
}
return arr;
}
var arr = [49,38,65,97,76,13,27,49,55,04];
shellSort(arr, Math.floor(arr.length / 2));function shellSort(arr) {
var len = arr.length;
for(var increment = Math.floor(len / 2); increment > 0; increment = Math.floor(increment / 2)) {
for(var i = increment; i = 0 && arr[j] > arr[j + increment]; j -= increment) {
var temp = arr[j];
arr[j] = arr[j + increment];
arr[j + increment] = temp;
}
}
}
return arr;
}
var arr = [49,38,65,97,76,13,27,49,55,04];
shellSort(arr);第一步: 将一个数组以中间值截取为为两个数组,分别将其排好序;
第二步: 申请一个空间,使其大小为两个已经排序的序列之和,该空间用来存放合并后的序列;
第三步: 设定两个指针,分别指向两个已排序序列的起始位置;
第四步: 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置.
重复第四步直到有一个某一指针超出序列尾;
将另一序列的所有元素复制到合并序列尾.
归并排序是稳定的,它在不会改变原来相等的元素的顺序.
平均情况下的时间复杂度: O(nlog₂n);
最好情况下的时间复杂度: O(nlog₂n) ;

var result = [];
function mergeArray(left, right) {
result = [];
while(left.length > 0 && right.length > 0) {
if(left[0] <p>相信看了本文案例你已经掌握了方法,更多精彩请关注php中文网其它相关文章!</p><p>推荐阅读:</p><p><a href="//m.sbmmt.com/js-tutorial-398003.html" target="_blank">React结合TypeScript和Mobx步骤详解</a><br></p><p><a href="//m.sbmmt.com/js-tutorial-398045.html" target="_blank">react实现选中li高亮步骤详解</a><br></p>以上是前端中排序演算法實例詳解的詳細內容。更多資訊請關注PHP中文網其他相關文章!




