堆排序(Heapsort)是指利用堆積樹(堆)這種資料結構所設計的一種排序演算法,它是選擇排序的一種。可以利用陣列的特性快速定位指定索引的元素。堆分為大根堆和小根堆,是完全二元樹。大根堆的要求是每個節點的值都不大於其父節點的值,即A[PARENT[i]] >= A[i]。在陣列的非降序排序中,需要使用的就是大根堆,因為根據大根堆的要求可知,最大的值一定在堆頂。
堆的定義
在一個完全二元樹中,任一父結點總是大於或等於(小於或等於)任何一個子節點,則為大頂堆(小頂堆)。
完全二元樹適合採用順序儲存的方式,因此一個陣列可以看成一個完全二元樹。
節點編號:樹根起,從上層到下層,每層從左到右,給所有結點順序編號,能得到一個反映整個二元樹結構的線性序列。
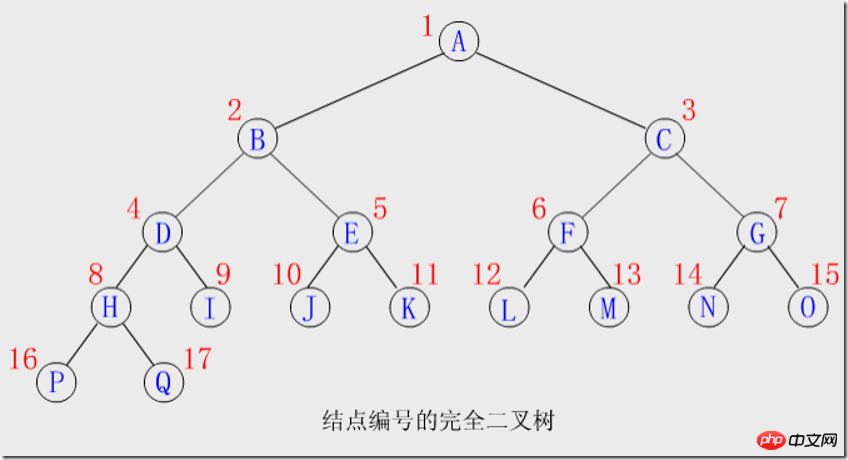
編號特徵:
從一個結點的編號就可推得其雙親,左、右孩子,兄弟等結點的編號。假設編號為i的結點為ki(1≤i≤n),則有:
①若i>1,則ki的雙親編號為i/2;若i=1,則Ki是根結點,無雙親。
②若2i≤n,則Ki的左孩子的編號是2i;否則,Ki無左孩子,即Ki必定是葉子。因此完全二元樹中編號i>n/2的結點必定是葉結點。
③若2i+1≤n,則Ki的右孩子的編號是2i+1;否則,Ki無右孩子。
註:ki(0≤i≤n)滿足數組下標時,則可能的左右孩子分別為2i+1、2i+2。
利用堆頂記錄的是最大關鍵字這一特性,每一輪取堆頂元素放入有序區,就類似選擇排序每一輪選擇一個最大值放入有序區,可以把堆排序看成是選擇排序的改進。
將初始待排序關鍵字序列(R0,R1,R2....Rn)建構成大頂堆,此堆為初始的無序區;
將堆頂元素R[0]與最後一個元素R[n]交換,此時得到新的無序區(R0,R1,R2,......Rn-1 )和新的有序區(Rn);
由於交換後新的堆頂R[0]可能違反堆的性質,因此需要對當前無序區(R0, R1,R2,......Rn-1)調整為新堆。
不斷重複此2、3步驟直到有序區的元素個數為n-1,則整個排序過程完成。
演算法分析
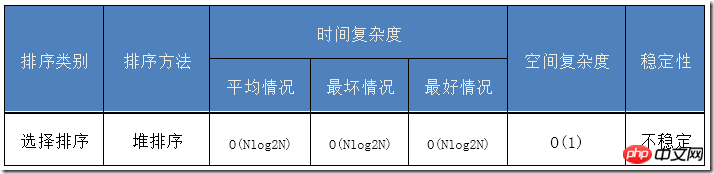
//最難理解的地方
目標:一個所有子樹都為堆的完全二元樹。意思就是這個二元樹只差跟節點不滿足堆的結構。 //很重要,很重要,很重要
如下圖:
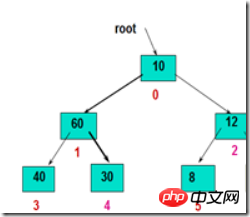
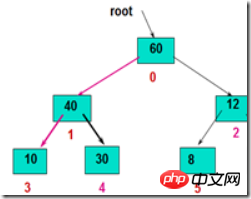
php实现堆排序:
<?php
//堆排序,对简单排序的改进
function swap(array &$arr,$a,$b)
{
$temp=$arr[$a];
$arr[$a]=$arr[$b];
$arr[$b]=$temp;
}
//调整$arr[$start]的关键字,$arr[$start]、$arr[$start+1]、、、$arr[$end]成为一个大根堆(根节点最大的完全二叉树)
//注意:这里节点s的左右孩子是 2*s +1 和 2*s+2(数组开始下标为0时)
function HeapAdjust(array &$arr $start $end)
{
$temp= $arr[$start];
//沿关键字较大的孩子节点向下筛选
//左右孩子计算 (这里数组的开始下标为0)
//左边孩子 2*$start+1,右边孩子 2*$start+2
for ($j=2*$start+1; $j <=$end; $j=2*$j+1) {
if ($j !=$end &&$arr[$j] <$arr[$j+1]) {
$j++; //转化为右边孩子
}
if ($temp >=$arr[$j]) {
break; //已经满足大根堆
}
//将根节点设置为子节点的较大值
$arr[$start]=$arr[$j];
//继续往下
$start=$j;
}
$arr[$start] =$temp;
}
function HeapSort(array &$arr)
{
$count=count($arr);
//先将数据结构造成大根堆 (由于是完全二叉树,所以这里用floor($count/2-1),下标小于或等于这个数的节点都是有孩子的节点)
for ($i=floor($count /2)-1; $i >=0 ; $i--) {
HeapAdjust($arr,$i,$count);
}
for ($i=$count-1; $i >=0 ; $i--) {
//将堆顶元素与最后一个元素交换,获取到最大元素(交换后的最后一个元素),将最大元素放到数组末尾
swap($arr,0,$i);
//经过交换,将最后一个元素(最大元素)脱离大根堆,并将未经排序的新数($arr[0...$i-1])重新调整为大根堆
HeapAdjust($arr,0,$i-1);
}
}
$arr=array(4,1,5,9);
HeapSort($arr);
v以上是php堆排序詳解的詳細內容。更多資訊請關注PHP中文網其他相關文章!




