最長公共子序是從給定的兩個序列X和Y中取出盡可能多的一部分字符,按照它們在原序列排列的先後次序排列得到。 LCS問題的演算法用途廣泛,如在軟體不同版本的管理中,用LCS演算法找到新舊版本的異同處;在軟體測試中,用LCS演算法對錄製和回放的序列進行比較,在基因工程領域,用LCS演算法檢查病人DNA連與鍵康DNA鏈的異同;在防抄襲系統中,用LCS演算法檢查論文的抄襲率。 LCS演算法也可以用於程式碼相似度度量,人體運行的序列檢索,視頻段匹配等方面,所以對LCS演算法進行研究具有很高的應用價值。
子序列(subsequence): 一個特定序列的子序列就是將給定序列中零個或多個元素去掉後得到的結果(不改變元素間相對次序)。例如序列
公共子序列(common subsequence): 給定序列X和Y,序列Z是X的子序列,也是Y的子序列,則Z是X和Y的公共子序列。例如X=[A,B,C,B,D,A,B],Y=[B,D,C,A,B,A[,則序列Z=[B,C,A]為X和Y的公共子序列,其長度為3。但Z不是X和Y的最長公共子序列,而序列[B,C,B,A]和[B,D,A,B]也均為X和Y的最長公共子序列,長度為4 ,而X和Y不存在長度大於等於5的公共子序列。對於序列[A,B,C]和序列[E,F,G]的公共子序列只有空序列[]。
最長公共子序列:給定序列X和Y,從它們的所有公共子序列中選出長度最長的那一個或幾個。
子字串: 將一個序列從最前或最後或同時刪除零個或幾個字元所構成的新系列。區別與子序列,子序列是可以從中間摳掉字元的。 cnblogs這個字串中子序列有多少個呢?很顯然有27個,例如其中的cb,cgs等等都是其子序列
給一個圖再解釋一下:
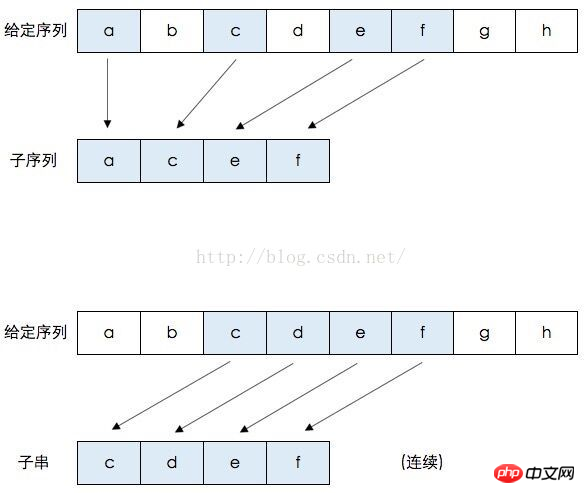
我們可以看出子序列不見得一定是連續的,連續的是子字串。
我們還是從一個矩陣開始分析,自己推導出狀態遷移方程式。
首先,我們把問題轉換成前端夠為熟悉的概念,不要序列序列地叫了,可以認為是陣列或字串。一切從簡,我們就估且認定是兩個字串做比較吧。
我們專注於留意」子序列「的概念,它可以刪掉多個或零個,也可以全部幹掉。這時我們的第一個子序列為 空字串 (如果我們的序列不是字串,我們還可以 )!這個真是千萬要注意到!許多人就是看不懂《演算法導論》的那張圖表,還有許多部落格的作者不懂裝懂。我們總是從左到右比較,當然了第一個字串,由於作為矩陣的高,就垂直放置了。
| x | "" | B | ##DC | A | B | A | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| #B | 假令X = "ABCDAB", Y="BDCABA",各自取出最短的序列,也就是空字串與空字串比較。 LCS的方程式解為一個數字,那麼這個表格也只能填數字。兩個空字串的公同區域的長度為0. | x | "" | B | #D | CA | B | A||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| "" | 0|||||||||||||
然後我們X不動,繼續讓空字符串出陣,Y讓“B”出陣,很顯然,它們的公共區域的長度為0. Y換成其他字符, D啊,C啊, 或者, 它們的連續組合DC、 DDC, 情況沒有變, 依然為0. 因此第一行都為0. 然後我們Y不動,Y只出空字任串,那麼與上面的分析一樣,都為0,第一列都是0.
| x | "" | B | D | #C | A | B | A | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ##"" | ##0 | #0 | 0 | 00 | 0 | 0||||||||
| #A | 0 | ||||||||||||
| B | 0 | ||||||||||||
| C | |||||||||||||
#D
0
| ##0 | B | 0 | LCS問題與背包問題有點不一樣,背包問題還可以設定-1行,而最長公共子序列因為有空子序列的出現,一開始就把左邊與上邊固定死了。 | 然後我們再將問題放大些,這次雙方都出一個字符,顯然只有兩都相同時,才有存在不為空字符串的公共子序列,長度也理解數然為1。 | A為"X", Y為"BDCA"的子序列的任一 | x | ##""B | D | CA | B ##A | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
0 | 0 | 0#0 | 0 ##0 | ||||||||||
| #0 | |||||||||||||
| 1 | |||||||||||||
| B | |||||||||||||
| ##D | 0 | A | 0 | B | ##0 | x | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | A | B | A | ||||||||||
| "" | 0 | ##0#0 | 0 | 0 | 0 | #0 | | ||||||
| 0 | 0 | ||||||||||||
| 0 | #1 | ||||||||||||
| ##1 | |||||||||||||
| #B | 0 | #C | 0 | D | 0 | A | 0 | #B | ##0|||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | "" | B | ##DC | A | B | A | |||||||
| "" | 0##0 | #00 | 0 | 0#0 | |||||||||
然後我們讓Y多出一個D做幫手,{"",A,B,AB} vs {"",B,D,BD},顯然,繼續填1. 一直填到Y的第二個B之前,都是1。 因為到BDCAB時,它們有另一個公共子序列,AB。
| x | "" | B | ##DC | A | B | A | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| "" | 0 | ##0#0 | 0 | 0 | 0#0 | ||||||||
0 | 0 | 00 | |||||||||||
| 1 | ##1|||||||||||||
| 0 | 1 | ||||||||||||
| 1 | 1 | ||||||||||||

| 0 | A | 0 | B | 0 | #到這一步,我們可以總結一些規則了,之後就是透過計算驗證我們的想法,加入新的規則或限定條件來完善。 | Y將所有字符派上去,X依然是2個字符,經仔細觀察,還是填2. | 看五行,X再多派一個C,ABC的子序列集合比AB的子序列集合大一些,那麼它與Y的B子序列集合大一些,就算不大,就不能比原來的小。顯然新增的C不能成為戰力,不是兩者的公共字符,因此值應該等於AB的子序列集合。 × | "" | B|||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | A | |||||||||||
| #"" | 0 | ##0 | 0 | 0 | 0 | 0 | #0 | ||||||
| A | 0 | 0 | 0 | 0 | #1 | 1 | 1 | ||||||
| B | 0 | ||||||||||||
| #1 | 1 | ||||||||||||
| 2 | 2 | ||||||||||||
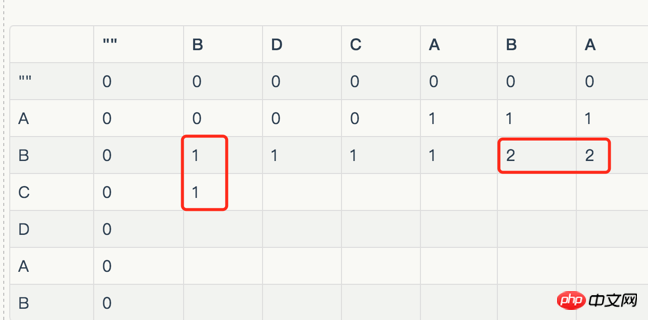
而且我們可以確定,如果兩個字串要比較的字元不一樣,那麼要填的格子是與其左邊或上邊有關,那邊大就取那個。
如果比較的字元一樣呢,稍安毋躁,剛好X的C要與Y的C進行比較,即ABC的子序列集合{"",A,B,C,AB,BC, ABC}與BDC的子序列集合{"",B,D,C,BD,DC,BDC}比較,得到公共子字串有「」,B,D 。這時還是與先前的結論一樣,當字元相等時,它對應的格子值等於左邊與右邊與左上角的值,並且左邊,上邊,左上邊總是相等的。這些奧秘需要更嚴格的數學知識來論證。
假设有两个数组,A和B。A[i]为A的第i个元素,A(i)为由A的第一个元素到第i个元素所组成的前缀。m(i, j)为A(i)和B(j)的最长公共子序列长度。
由于算法本身的递推性质,其实只要证明,对于某个i和j:
m(i, j) = m(i-1, j-1) + 1 (当A[i] = B[j]时)
m(i, j) = max( m(i-1, j), m(i, j-1) ) (当A[i] != B[j]时)
第一个式子很好证明,即当A[i] = B[j]时。可以用反证,假设m(i, j) > m(i-1, j-1) + 1 (m(i, j)不可能小于m(i-1, j-1) + 1,原因很明显),那么可以推出m(i-1, j-1)不是最长的这一矛盾结果。
第二个有些trick。当A[i] != B[j]时,还是反证,假设m(i, j) > max( m(i-1, j), m(i, j-1) )。
由反证假设,可得m(i, j) > m(i-1, j)。这个可以推出A[i]一定在m(i, j)对应的LCS序列中(反证可得)。而由于A[i] != B[j],故B[j]一定不在m(i, j)对应的LCS序列中。所以可推出m(i, j) = m(i, j-1)。这就推出了与反正假设矛盾的结果。
得证。</p>
<p> </p>
<p>我們現在用下面的方程式來繼續填表了。 </p>
<p><img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/article/000/054/025/4261b59f87cbe8cff3afd0492985a179-3.png" class="lazy" alt="詳談javascript最長公共子序列" ></p>
<h2>程式實現</h2>
<pre class="brush:php;toolbar:false">//by 司徒正美
function LCS(str1, str2){
var rows = str1.split("")
rows.unshift("")
var cols = str2.split("")
cols.unshift("")
var m = rows.length
var n = cols.length
var dp = []
for(var i = 0; i < m; i++){
dp[i] = []
for(var j = 0; j < n; j++){
if(i === 0 || j === 0){
dp[i][j] = 0
continue
}
if(rows[i] === cols[j]){
dp[i][j] = dp[i-1][j-1] + 1 //对角+1
}else{
dp[i][j] = Math.max( dp[i-1][j], dp[i][j-1]) //对左边,上边取最大
}
}
console.log(dp[i].join(""))//调试
}
return dp[i-1][j-1]
}
LCS可以進一步簡化,只要透過挪位置,省去新陣列的產生
//by司徒正美
function LCS(str1, str2){
var m = str1.length
var n = str2.length
var dp = [new Array(n+1).fill(0)] //第一行全是0
for(var i = 1; i <= m; i++){ //一共有m+1行
dp[i] = [0] //第一列全是0
for(var j = 1; j <= n; j++){//一共有n+1列
if(str1[i-1] === str2[j-1]){
//注意这里,str1的第一个字符是在第二列中,因此要减1,str2同理
dp[i][j] = dp[i-1][j-1] + 1 //对角+1
} else {
dp[i][j] = Math.max( dp[i-1][j], dp[i][j-1])
}
}
}
return dp[m][n];
}
我們再來給列印函數,先看如何列印一個。我們從右下角開始尋找,一直找到最上一行終止。因此目標字串的建構是倒序。為了避免使用stringBuffer這樣麻煩的中間量,我們可以透過遞歸實現,每次執行程式時,只回傳一個字串,沒有則回傳一個空字串, 以 printLCS(x,y,...) + str[ i] 相加,就可以得到我們要求的字串。
我們再寫出一個方法,來驗證我們得到的字串是否真正的LCS字串。作為一個已經工作的人,不能寫的程式碼像在校生那樣,不做單元測試就放到線上讓別人踩坑。
//by 司徒正美,打印一个LCS
function printLCS(dp, str1, str2, i, j){
if (i == 0 || j == 0){
return "";
}
if( str1[i-1] == str2[j-1] ){
return printLCS(dp, str1, str2, i-1, j-1) + str1[i-1];
}else{
if (dp[i][j-1] > dp[i-1][j]){
return printLCS(dp, str1, str2, i, j-1);
}else{
return printLCS(dp, str1, str2, i-1, j);
}
}
}
//by司徒正美, 将目标字符串转换成正则,验证是否为之前两个字符串的LCS
function validateLCS(el, str1, str2){
var re = new RegExp( el.split("").join(".*") )
console.log(el, re.test(str1),re.test(str2))
return re.test(str1) && re.test(str2)
}
使用:
function LCS(str1, str2){
var m = str1.length
var n = str2.length
//....略,自行补充
var s = printLCS(dp, str1, str2, m, n)
validateLCS(s, str1, str2)
return dp[m][n]
}
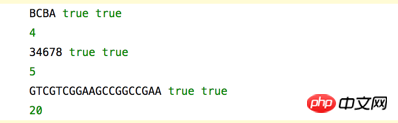
var c1 = LCS( "ABCBDAB","BDCABA");
console.log(c1) //4 BCBA、BCAB、BDAB
var c2 = LCS("13456778" , "357486782" );
console.log(c2) //5 34678
var c3 = LCS("ACCGGTCGAGTGCGCGGAAGCCGGCCGAA" ,"GTCGTTCGGAATGCCGTTGCTCTGTAAA" );
console.log(c3) //20 GTCGTCGGAAGCCGGCCGAA
//by 司徒正美 打印所有LCS
function printAllLCS(dp, str1, str2, i, j){
if (i == 0 || j == 0){
return new Set([""])
}else if(str1[i-1] == str2[j-1]){
var newSet = new Set()
printAllLCS(dp, str1, str2, i-1, j-1).forEach(function(el){
newSet.add(el + str1[i-1])
})
return newSet
}else{
var set = new Set()
if (dp[i][j-1] >= dp[i-1][j]){
printAllLCS(dp, str1, str2, i, j-1).forEach(function(el){
set.add(el)
})
}
if (dp[i-1][j] >= dp[i][j-1]){//必须用>=,不能简单一个else搞定
printAllLCS(dp, str1, str2, i-1, j).forEach(function(el){
set.add(el)
})
}
return set
}
}function LCS(str1, str2){
var m = str1.length
var n = str2.length
//....略,自行补充
var s = printAllLCS(dp, str1, str2, m, n)
console.log(s)
s.forEach(function(el){
validateLCS(el,str1, str2)
console.log("输出LCS",el)
})
return dp[m][n]
}
var c1 = LCS( "ABCBDAB","BDCABA");
console.log(c1) //4 BCBA、BCAB、BDAB
var c2 = LCS("13456778" , "357486782" );
console.log(c2) //5 34678
var c3 = LCS("ACCGGTCGAGTGCGCGGAAGCCGGCCGAA" ,"GTCGTTCGGAATGCCGTTGCTCTGTAAA" );
console.log(c3) //20 GTCGTCGGAAGCCGGCCGAA
function LCS(str1, str2){
var m = str1.length
var n = str2.length
var dp = [new Array(n+1).fill(0)],now = 1,row //第一行全是0
for(var i = 1; i <= m; i++){ //一共有2行
row = dp[now] = [0] //第一列全是0
for(var j = 1; j <= n; j++){//一共有n+1列
if(str1[i-1] === str2[j-1]){
//注意这里,str1的第一个字符是在第二列中,因此要减1,str2同理
dp[now][j] = dp[i-now][j-1] + 1 //对角+1
} else {
dp[now][j] = Math.max( dp[i-now][j], dp[now][j-1])
}
}
now = 1- now; //1-1=>0;1-0=>1; 1-1=>0 ...
}
return row ? row[n]: 0
}
危險的遞歸解法
//警告,字符串的长度一大就会爆栈
function LCS(str1, str2, a, b) {
if(a === void 0){
a = str1.length - 1
}
if(b === void 0){
b = str2.length - 1
}
if(a == -1 || b == -1){
return 0
}
if(str1[a] == str2[b]) {
return LCS(str1, str2, a-1, b-1)+1;
}
if(str1[a] != str2[b]) {
var x = LCS(str1, str2, a, b-1)
var y = LCS(str1, str2, a-1, b)
return x >= y ? x : y
}
}相關建議:
用Python語言描述最大連續子序列和以上是詳談javascript最長公共子序列的詳細內容。更多資訊請關注PHP中文網其他相關文章!




