俗話說:發圖不留種,菊花萬人捅!我這裡想延伸一下:教學不給例,說你是傻逼!哎呀,還挺押韻,嘻嘻,開個玩笑!
我們都講了四期API的知識了,估計大家看的也是枯燥的很啊,前面的小實例也是太簡單,簡直不解渴啊,但是也不能一口氣就吃成一個胖子,下面再給大家來一個小實例,給大家提提神!
前面在講畫圓的時候,給大家留了一個思考,或者說是一個坑吧,就是如何來畫一個扇形?我們知道畫圓的方法是無法一下子就能畫出一個扇形的,我當時提供了一個方法,不知道大家是否有印象,沒印象沒關係,我再復述一遍:就是如果我畫了一個圓弧,然後在圓心畫2條線,分別連在圓弧的起始點和結束點,那不就是一個圓嗎?那麼這個方法到底能不能畫出一個圓呢?其實我也不知道,那我們就試試看:
第一步,畫一個圓弧:
//将原点移到100,100的位置 ctx.translate(100, 100); //画一个圆弧 ctx.arc(0,0,100,30*Math.PI/180, 60*Math.PI/180); ctx.stroke();

##此時就是我們熟悉的畫圓弧的方法,現在要開始畫線了,這才是關鍵,我們先分析一下,磨刀不費砍柴工嘛!
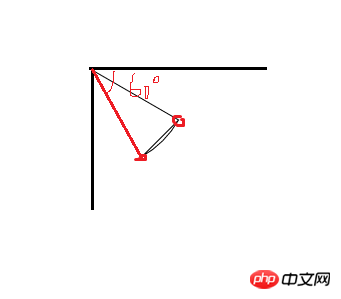
一條直線是由2個點構成,現在我們知道圓心這點,第2個點就是圓弧的起始點和結束點,那麼這2的座標我們怎麼得到呢?我們畫圖來分析一下: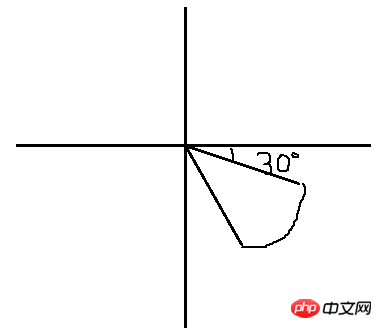
我們大概就是要畫這樣一個扇形,畫的比較醜,將就看一下,如果我們按照數學思路,根據角度公式一通算,或許能得到這2個點的座標,但是我感覺我自己想想都覺得這運算該有多麼的複製,我數學不好,不願意算,有沒有一種簡便的方法呢,可以不用那麼的懂腦筋的? (抱歉,我的「記憶體」明顯感到不足)我有一個大膽的假設,就是如果這個扇形不是這樣斜著的,而是一邊的水平的,比如說這樣: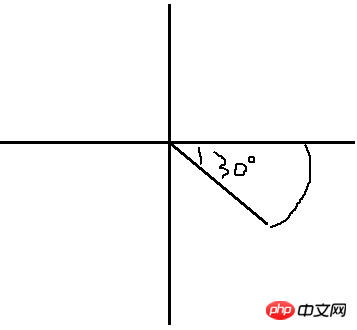
那我就可以很容易的得到第一條線段了,就是橫座標上的那條線,你不懂?好吧,是這樣的,圓心座標我們知道,半徑我們知道,那弧的起點座標就很容易啦,懂了吧,那另一條線怎麼弄呢?如果你剛看完上一期API的知識,我們趁熱,很容易就能想到rotate()方法,就是我們再畫一條圓心到起點的線,圓弧的角度我們是知道的,好,我們將新畫的這條線選擇圓弧的角度,不就到終點了嗎?我靠,我TM太機智了!讓我們來試試看:
//圆弧 ctx.save(); ctx.translate(100, 100); ctx.arc(0,0,100,0, 30*Math.PI/180); ctx.restore(); //第一条线 ctx.save(); ctx.moveTo(100,100); ctx.lineTo(200,100); ctx.restore(); //第二条线 ctx.save(); ctx.translate(100, 100); ctx.moveTo(0,0); ctx.rotate(30*Math.PI/180); ctx.lineTo(100,0); ctx.stroke(); ctx.restore();
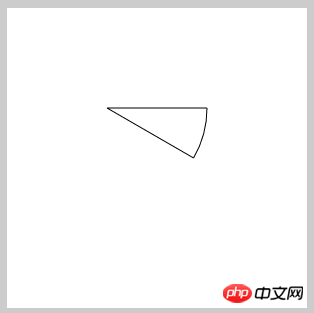
#哇塞,簡直眼前一亮啊,果然可以啊,按照這思路,如果我們現在把這個扇形旋轉一個角度,這個角度=第二條線的角度-第一條線的角度,那麼得到的不就是前面我們需要的那個扇形嗎?但是前面的程式碼直接旋轉只能旋轉圓弧,線旋轉不了,我們修改一下:
#還是看這張圖吧,我們可以換個思路,如果圓弧畫在目標位置,然後畫2條角度為0的2條線,再旋轉到圓弧的起始點和結束點,不就行了嗎? (因為圓弧的起始角度和結束角度我們是知道的)試試看:
//将原点设置100,100位置 ctx.translate(100,100); //原点在100,100,则圆心设为0,0 ——> 100,100的位置 ctx.arc(0,0,100,30*Math.PI/180,60*Math.PI/180); //save(),restore()是为了防止角度旋转的污染 ctx.save(); ctx.rotate(30*Math.PI/180); ctx.moveTo(0,0); ctx.lineTo(100,0); ctx.restore(); ctx.rotate(60*Math.PI/180); ctx.moveTo(0,0); ctx.lineTo(100,0); ctx.stroke();

哎呀,真的可以啊,哈哈,有人会问,你的第一步为什么是设置原点呢,为什么不用moveTo来设置起始点呢?好问题,因为画布的默认原点在0,0的位置上,如果用moveTo来设置起始点,原点依然还在0,0的位置,上一节API我们将变换的时候讲到,变换是以原点为基准点的,即使你设置了起始点,但是起始点不是原点的话,图形旋转依然会围绕0,0点旋转然后自转,得到的图形就不知道是什么图形了,偏差的角度就很难矫正,对此还是不太明白的同学可以自己写一个例子体验一样,或许理解更深刻一点,这里就作为练习题,不在这里写了!
上面的代码还是可以优化的,比如说画第一条线的时候,我们用到了save()和restore(),其作用不只是可以防止外面的属性或方法对里面的绘制产生影响,它的本质意思是save()保存当前环境的状态,restore()返回之前保存路径的状态,这是什么意思,举个栗子,save()就像是在一个迷宫的入口,restore()就想是这个迷宫的出口,但是发现这里就是迷宫的路口,出了迷宫,在迷宫里具体是怎么走的,根本不知道,这就可以防止你的外部因素来影响你走迷宫的路线,那有一个细节大家要注意,就是当你进去的这个门,你出来的时候还是这个门,恩,这个就可以利用了,这就相当于是画笔的触点了,还原触点,我们看一下还原的触点在什么地方:
//将原点设置100,100位置 ctx.translate(100,100); //原点在100,100,则圆心设为0,0 ——> 100,100的位置 ctx.arc(0,0,100,30*Math.PI/180,60*Math.PI/180); //save(),restore()是为了防止角度旋转的污染 ctx.save(); ctx.rotate(30*Math.PI/180); ctx.moveTo(0,0); ctx.lineTo(100,0); ctx.restore(); ctx.rotate(60*Math.PI/180); ctx.lineTo(100,0); ctx.stroke();
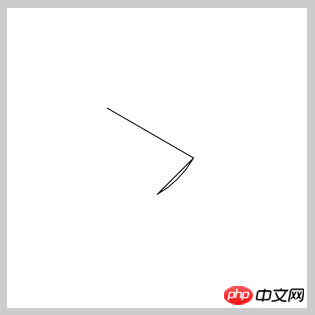
居然得到的是这样的结果,从第2张图可以看出还原的触点的位置在圆弧的初始点,其实这里我们是忽略了一个问题,就是线在旋转的时候,是从它的起点为圆心旋转的,而上面的代码是,第一条线从圆心开始,到圆弧的起点(旋转过后),自然现在的起点就是圆弧的起点了,第二条线怎么画,它旋转的结果都不是我们想要的了,所以这里我们需要特别的注意,现在我们将第一条直线的起点设在(r,0)的位置,旋转后就到了圆弧的起始点,然后在画到圆心地方,那现在的起始点就是圆心了,再画一条线到圆弧,就哦了,现在我们再来一次:
//将原点设置100,100位置 ctx.translate(100,100); //原点在100,100,则圆心设为0,0 ——> 100,100的位置 ctx.arc(0,0,100,30*Math.PI/180,60*Math.PI/180); //save(),restore()是为了防止角度旋转的污染 ctx.save(); ctx.rotate(30*Math.PI/180); ctx.moveTo(100,0); ctx.lineTo(0,0); ctx.restore(); ctx.rotate(60*Math.PI/180); ctx.lineTo(100,0); ctx.stroke();

看,这就是我们想要的图形,所以,上面所犯的几个错都是比较容易犯的错,需要特别的注意!
根据这个原理,我们其实还可以用另外一种方式,就是充分使用触点的作用,怎么讲,当我们再画圆弧的时候,画完之后其触点在圆弧的结束位置,如此的天赐良机,为何不直接将这个触点作为起点,画一条到圆心的线,不就可以少旋转一次吗?然后再画第二条线,简直感觉省时省力,我们看看效果吧:
//将原点设置100,100位置 ctx.translate(100,100); //原点在100,100,则圆心设为0,0 ——> 100,100的位置 ctx.arc(0,0,100,30*Math.PI/180,60*Math.PI/180); //以圆弧终点为起点画直线 ctx.lineTo(0,0); ctx.rotate(30*Math.PI/180); //以0,0为起点画直线 ctx.lineTo(100,0); ctx.stroke();

你看,用这个理论,就连save(),restore()都可以省了,因为就只有一个旋转,代码也少了好多,效果还一样,哈哈,为了能重复使用,我们需要把他封装一下:
第一种:
CanvasRenderingContext2D.prototype.sector = function(x,y,r,sDeg,eDeg){
this.save();
this.translate(x,y);
this.beginPath();
this.arc(0,0,r,sDeg*Math.PI/180,eDeg*Math.PI/180);
this.save();
this.rotate(sDeg*Math.PI/180);
this.moveTo(r,0);
this.lineTo(0,0);
this.restore();
this.rotate(eDeg*Math.PI/180);
this.lineTo(r,0);
this.restore();
return this;
}
ctx.sector(100,100,100,30,60).stroke();
ctx.sector(100,100,100,90,120).fill();
ctx.sector(100,100,100,160,180).stroke();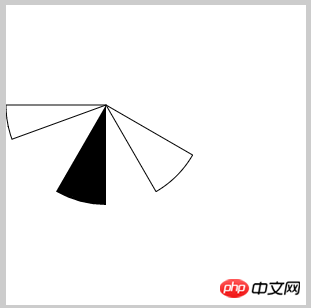
第二种:
CanvasRenderingContext2D.prototype.sector = function(x,y,r,sDeg,eDeg){
this.save();
this.translate(x,y);
this.beginPath();
this.arc(0,0,r,sDeg*Math.PI/180,eDeg*Math.PI/180);
this.lineTo(0,0);
this.rotate(sDeg*Math.PI/180);
this.lineTo(r,0);
this.restore();
return this;
}
ctx.sector(100,100,100,30,60).stroke();
ctx.sector(100,100,100,90,120).fill();
ctx.sector(100,100,100,160,180).stroke();
你以为这样就完了吗?当我们充分理解canvasAPI的基础知识的时候,我们还会得到另外一种方式来画扇形,简直6到爆!哈哈哈!究竟是什么呢?我们接着往下看:
前面的基础知识讲到画圆的时候,我们讲到了beginPath()和closePath(),有人会说,这不就是开始路径和封闭路径吗?这跟画扇形有什么关系?没错,你说的一点都没错,好,现在请大声跟我念:封闭路径!封闭路径!封闭路径!重要事情说3遍,现在你的心里是不是有了那么一点感觉,没错,不要觉得害羞,不要觉得压抑,就是它,就是它,大声把它说出来,就是这感觉,什么?你什么感觉都没有,此处有表情,好吧,我来告诉你我的感觉:
上面有一处说,为什么要用translate,而不要moveTo,是因为我们需要旋转,所以就需要原点,现在如果我们不需要旋转,而是正常的画图,那么我们就不需要原点,我们就可以用moveTo,好了,如果我们配合beginPath()和closePath(),就会将一个圆弧封闭起来,想想我们在讲画三角形的时候的那段折线是怎么变成三角形的,没错,现在是否有了一点感觉?还是木有?好吧,我们来看一个栗子:
ctx.beginPath(); //定义起点 ctx.moveTo(100,100); //以起点为圆心,画一个半径为100的圆弧 ctx.arc(100,100,100,30*Math.PI/180, 60*Math.PI/180); ctx.closePath(); ctx.stroke();

看看,寥寥数行,就画出了一个扇形,对不上面的图像,是不是一样的?我们封装一下:
CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
this.save();
this.beginPath();
this.moveTo(x,y);
this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
this.closePath();
this.restore();
return this;
}
ctx.sector(100,100,100,30,60).stroke();
ctx.sector(100,100,100,90,120).fill();
ctx.sector(100,100,100,160,180).stroke();
效果都一样,只是思路不一样,或许还有别的方式来画扇形,如果大家有更好的方法,希望能留下你的代码,大家互相学习一下!
扇形的方法有了,具体用哪个可以依据自己的喜好,我就按照第3种来写一个小应用,饼图:
CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
this.save();
this.beginPath();
this.moveTo(x,y);
this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
this.closePath();
this.restore();
return this;
}
ctx.fillStyle = 'red';
ctx.sector(200,200,100,30,150).fill();
ctx.fillStyle = 'green';
ctx.sector(200,200,100,150,270).fill();
ctx.fillStyle = 'blue';
ctx.sector(200,200,100,270,390).fill();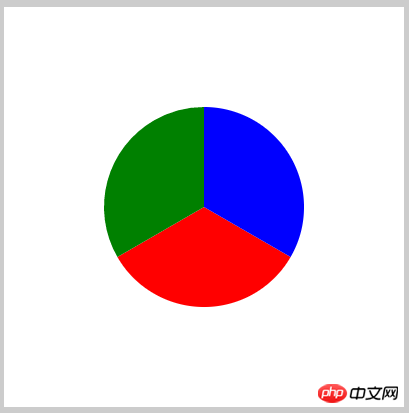
再写一个扇形倒计时:
CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
this.save();
this.beginPath();
this.moveTo(x,y);
this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
this.closePath();
this.restore();
return this;
}
var angle = 0;
var timer = null;
ctx.fillStyle = 'green';
setInterval(function(){
angle+=5;
ctx.sector(200,200,100,0,angle).fill();
if(angle == 360){
clearInterval(timer);
}
},200);
你以为我只是写几个例子给你看吗?你还是太年轻了,之所以要丢出这2个例子,是为了扩展一下思路,我们可以在这些效果上面加一点什么东西,效果是否就不一样了,举个例子,第一个饼图,如果我们在中间加一个白色的圆,会怎么样?
CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
this.save();
this.beginPath();
this.moveTo(x,y);
this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
this.closePath();
this.restore();
return this;
}
ctx.fillStyle = 'red';
ctx.sector(200,200,100,30,150).fill();
ctx.fillStyle = 'green';
ctx.sector(200,200,100,150,270).fill();
ctx.fillStyle = 'blue';
ctx.sector(200,200,100,270,390).fill();
ctx.fillStyle = '#fff';
ctx.sector(200,200,80,0,360).fill();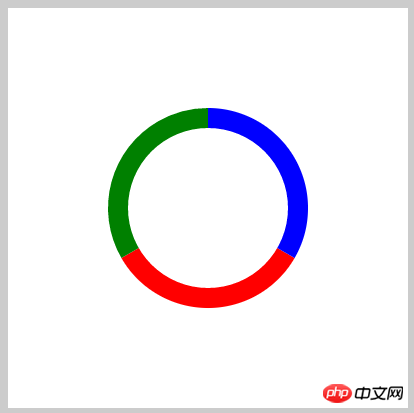
看,这效果是不是就变成另外一个效果了,比如说第二个效果,我们也加一个白色的圆,看有什么效果:
CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
this.save();
this.beginPath();
this.moveTo(x,y);
this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
this.closePath();
this.restore();
return this;
}
var angle = 0;
var timer = null;
setInterval(function(){
angle+=5;
ctx.fillStyle = 'green';
ctx.sector(200,200,100,0,angle).fill();
ctx.fillStyle = '#fff';
ctx.sector(200,200,80,0,360).fill();
if(angle == 360){
clearInterval(timer);
}
},200);
看看,这效果是不是可以做很多的效果,当然,因为没有加动画效果,现在的效果很生硬,需要大家来完善,只要你脑洞打开,其实扇形还是能做出很多非常炫酷的效果的,当然了,好的效果都是需要打磨的,在此只是抛砖引玉,如果大家有更好,更炫酷的效果,请不吝分享一下,今天就讲到这里,谢谢大家的支持!
以上就是canvas实践小实例二 —— 扇形 的内容,更多相关内容请关注PHP中文网(m.sbmmt.com)!




