閱讀前請看,謝謝!
關於卷積,在上一篇我們已經提到來,不明白的童鞋可以去看上一篇。
看到題目,聰明的童鞋應該明白他們直接的關係了。對於卷積運算,採取不同的模板(Mask),就能得到不同的結果,先實現卷積運算。
程式碼如下:
public void filter(double[][] mask) {
toGray();//灰度化
int mh = mask.length;
int mw = mask[1].length;
int sh = (mh+1)/2;
int sw = (mw+1)/2;
double maskSum = math.sum(mask);
int[] d= new int[w*h];
for(int i=(mh-1)/2+1;i<h-(mh-1)/2;i++){
for(int j=(mw-1)/2+1;j<w-(mw-1)/2;j++){
int s = 0;
for(int m=0; m<mh ; m++){
for(int n=0;n<mw;n++){
s = s + (int)(mask[m]
*this.data[j+n-sw +(i+m-sh)*w]);
}
}
if(maskSum != 0)
s /= maskSum;
if(s < 0)
s =0;
if(s > 255)
s = 255;
d[j + i * w] = s;
}
}
this.data = d;
}對於高斯核產生的高斯範本如下:

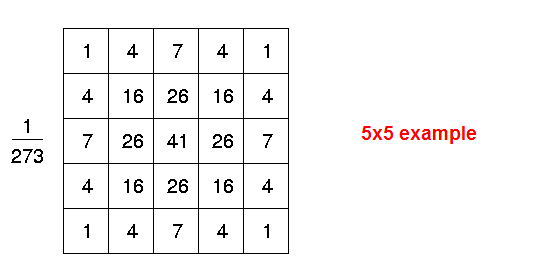
運行結果分別為,右邊
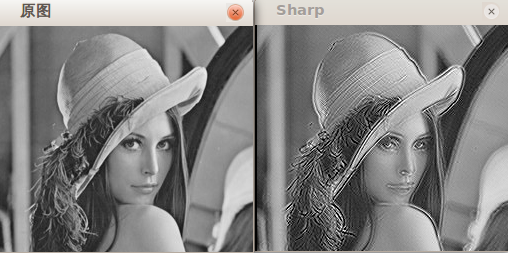
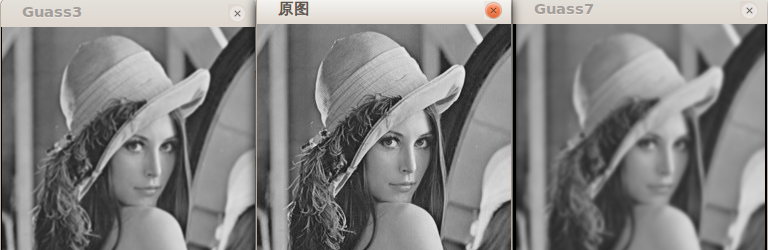 銳利化模板:
銳利化模板:
 運行結果:
運行結果:
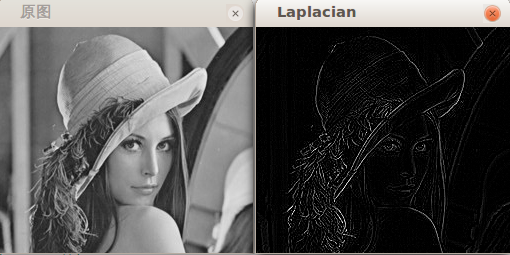
 拉普拉斯算子:
拉普拉斯算子:
 運轉拉斯算子的內容,更多相關內容請關注PHP中文網(m.sbmmt.com)!
運轉拉斯算子的內容,更多相關內容請關注PHP中文網(m.sbmmt.com)!