DeepSeek-V3解釋了1:多頭潛在註意力
DeepSeek-V3詳解系列文章之:多頭潛在註意力機制 (MLA)
本文是“DeepSeek-V3詳解”系列的第一篇文章,我們將深入探討DeepSeek最新開源模型DeepSeek-V3 [1, 2]。
本系列文章將涵蓋兩個主要主題:
- DeepSeek-V3的主要架構創新,包括MLA(多頭潛在註意力)[3]、DeepSeekMoE [4]、無輔助損失的負載均衡[5]以及多標記預測訓練。
- DeepSeek-V3的訓練過程,包括預訓練、微調和強化學習對齊階段。
本文主要關注多頭潛在註意力機制 (MLA),該機制最初在DeepSeek-V2的開發中提出,並在DeepSeek-V3中得到應用。
目錄:
- 背景: 我們將從標準MHA開始,解釋為什麼在推理階段需要鍵值緩存,MQA和GQA如何嘗試優化它,以及RoPE的工作原理等。
- 多頭潛在註意力機制 (MLA): 深入介紹MLA,包括其動機、為什麼需要解耦RoPE及其性能。
- 參考文獻。
背景
為了更好地理解MLA,並使本文自成一體,在深入探討MLA細節之前,我們將回顧本節中幾個相關的概念。
解碼器Transformer中的MHA
請注意,MLA的開發是為了加快自回歸文本生成的推理速度,因此在此上下文中討論的MHA是針對僅解碼器的Transformer。
下圖比較了三種用於解碼的Transformer架構,其中(a)顯示了原始“Attention is All You Need”論文中提出的編碼器和解碼器。其解碼器部分隨後被[6]簡化,得到(b)所示的僅解碼器的Transformer模型,該模型後來被許多生成模型(如GPT [8])使用。
如今,大型語言模型更常選擇(c)所示的結構以實現更穩定的訓練,在輸入而不是輸出上應用歸一化,並將LayerNorm升級為RMS Norm。這將作為我們本文中討論的基線架構。
 在此上下文中,MHA計算在很大程度上遵循[6]中的過程,如下圖所示:
在此上下文中,MHA計算在很大程度上遵循[6]中的過程,如下圖所示:
 假設我們有n_h個注意力頭,每個注意力頭的維度表示為d_h,因此連接後的維度將為(h_n · d_h)。
假設我們有n_h個注意力頭,每個注意力頭的維度表示為d_h,因此連接後的維度將為(h_n · d_h)。
對於具有l層的模型,如果我們將該層中第t個標記的輸入表示為維度為d的h_t,則需要使用線性映射矩陣將h_t的維度從d映射到(h_n · d_h)。
更正式地說,我們有(來自[3]的方程):
 其中W^Q、W^K和W^V是線性映射矩陣:
其中W^Q、W^K和W^V是線性映射矩陣:
 映射後,將q_t、k_t和v_t拆分為n_h個頭來計算比例點積注意力:
映射後,將q_t、k_t和v_t拆分為n_h個頭來計算比例點積注意力:
 其中W^O是另一個投影矩陣,用於將維度反向從(h_n · d_h)映射到d:
其中W^O是另一個投影矩陣,用於將維度反向從(h_n · d_h)映射到d:
 請注意,上述Eqn.(1)到(8)描述的過程僅針對單個標記。在推理過程中,我們需要對每個新生成的標記重複此過程,這涉及大量重複計算。這導致了一種稱為鍵值緩存的技術。
請注意,上述Eqn.(1)到(8)描述的過程僅針對單個標記。在推理過程中,我們需要對每個新生成的標記重複此過程,這涉及大量重複計算。這導致了一種稱為鍵值緩存的技術。
鍵值緩存
顧名思義,鍵值緩存是一種旨在通過緩存和重用以前的鍵和值來加快自回歸過程的技術,而不是在每個解碼步驟中重新計算它們。
請注意,KV緩存通常僅在推理階段使用,因為在訓練中我們仍然需要並行處理整個輸入序列。
KV緩存通常實現為滾動緩衝區。在每個解碼步驟中,僅計算新的查詢Q,而緩存中存儲的K和V將被重用,以便使用新的Q和重用的K、V計算注意力。同時,新標記的K和V也將添加到緩存中以供以後使用。
然而,鍵值緩存帶來的加速是以內存為代價的,因為鍵值緩存通常隨批大小× 序列長度× 隱藏大小× 頭數而變化,當我們有更大的批大小或更長的序列時,這會導致內存瓶頸。
這進一步導致了兩種旨在解決此限制的技術:多查詢注意力和分組查詢注意力。
多查詢注意力 (MQA) 與分組查詢注意力 (GQA)
下圖顯示了原始MHA、分組查詢注意力 (GQA) [10]和多查詢注意力 (MQA) [9]之間的比較。
 MQA的基本思想是跨所有查詢頭共享單個鍵和單個值頭,這可以顯著減少內存使用,但也將影響注意力的準確性。
MQA的基本思想是跨所有查詢頭共享單個鍵和單個值頭,這可以顯著減少內存使用,但也將影響注意力的準確性。
GQA可以看作是MHA和MQA之間的一種插值方法,其中只有一對鍵和值頭將僅由一組查詢頭共享,而不是所有查詢。但這仍然會導致比MHA更差的結果。
在後面的章節中,我們將看到MLA如何設法在內存效率和建模精度之間取得平衡。
RoPE(旋轉位置嵌入)
我們需要提到的最後一個背景知識是RoPE [11],它通過使用正弦函數旋轉多頭注意力中的查詢和鍵向量來直接將位置信息編碼到注意力機制中。
更具體地說,RoPE對每個標記的查詢和鍵向量應用位置相關的旋轉矩陣,並使用正弦和余弦函數作為其基,但以獨特的方式應用它們來實現旋轉。
要了解是什麼使其成為位置相關的,請考慮一個只有4個元素的玩具嵌入向量,即(x_1, x_2, x_3, x_4)。
要應用RoPE,我們首先將連續的維度分組為對:
- (x_1, x_2) -> 位置1
- (x_3, x_4) -> 位置2
然後,我們應用旋轉矩陣來旋轉每一對:
 其中θ = θ(p) = p ⋅ θ_0,而θ_0是基頻。在我們的4維玩具示例中,這意味著(x_1, x_2)將旋轉θ_0,而(x_3, x_4)將旋轉2 ⋅ θ_0。
其中θ = θ(p) = p ⋅ θ_0,而θ_0是基頻。在我們的4維玩具示例中,這意味著(x_1, x_2)將旋轉θ_0,而(x_3, x_4)將旋轉2 ⋅ θ_0。
這就是為什麼我們將此旋轉矩陣稱為位置相關的:在每個位置(或每一對)處,我們將應用一個不同的旋轉矩陣,其中旋轉角度由位置確定。
RoPE由於其在編碼長序列方面的效率而被廣泛用於現代大型語言模型,但正如我們從上述公式中看到的,它對Q和K都具有位置敏感性,這使得它在某些方面與MLA不兼容。
多頭潛在註意力機制
最後,我們可以繼續討論MLA部分。在本節中,我們將首先闡述MLA的高級思想,然後深入探討為什麼它需要修改RoPE。最後,我們還將介紹MLA的詳細算法及其性能。
MLA:高級思想
MLA的基本思想是將注意力輸入h_t壓縮為一個低維潛在向量,其維度為d_c,其中d_c遠小於原始的(h_n · d_h)。稍後,當我們需要計算注意力時,我們可以將此潛在向量映射回高維空間以恢復鍵和值。因此,只需要存儲潛在向量,從而顯著減少內存使用。
此過程可以用以下方程更正式地描述,其中c^{KV}_t是潛在向量,W^{DKV}是將h_t的維度從(h_n · d_h)映射到d_c的壓縮矩陣(此處上標中的D代表“降維投影”,表示壓縮維度),而W^{UK}和W^{UV}都是將共享潛在向量映射回高維空間的上投影矩陣。
 類似地,我們還可以將查詢映射到一個潛在的低維向量,然後將其映射回原始的高維空間:
類似地,我們還可以將查詢映射到一個潛在的低維向量,然後將其映射回原始的高維空間:
 ### 為什麼需要解耦RoPE
### 為什麼需要解耦RoPE
如前所述,RoPE是訓練生成模型以處理長序列的常用選擇。如果我們直接應用上述MLA策略,這將與RoPE不兼容。
為了更清楚地看到這一點,請考慮當我們使用Eqn. (7)計算注意力時會發生什麼:當我們將轉置的q與k相乘時,矩陣W^Q和W^{UK}將出現在中間,它們的組合相當於從d_c到d 的單個映射維度。
在原始論文[3]中,作者將其描述為W^{UK}可以被“吸收”到W^Q中,因此我們不需要在緩存中存儲W^{UK},從而進一步減少內存使用。
但是,當我們考慮圖(4)中的旋轉矩陣時,情況並非如此,因為RoPE將在W^{UK}的左側應用旋轉矩陣,並且此旋轉矩陣最終將位於轉置的W^Q和W^{UK}之間。
正如我們在背景部分所解釋的,此旋轉矩陣是位置相關的,這意味著每個位置的旋轉矩陣都不同。因此,W^{UK}**不能再被W^Q**吸收**。
為了解決這種衝突,作者提出了他們所謂的“解耦RoPE”,通過引入額外的查詢向量以及共享鍵向量,並且僅在RoPE過程中使用這些額外向量,同時保持原始鍵與旋轉矩陣某種程度上隔離。
整個MLA過程可以總結如下(方程編號從[3]的附錄C中重複使用):
 其中
其中
- Eqn. (37)到(40)描述瞭如何處理查詢標記。
- Eqn. (41)和(42)描述瞭如何處理鍵標記。
- Eqn. (43)和(44)描述瞭如何使用額外的共享鍵進行RoPE,請注意(42)的輸出不參與RoPE。
- Eqn. (45)描述瞭如何處理值標記。
在此過程中,只需要緩存帶有框的藍色變量。此過程可以用下面的流程圖更清晰地說明:
 ### MLA的性能
### MLA的性能
下表比較了KV緩存(每個標記)所需的元素數量以及MHA、GQA、MQA和MLA之間的建模能力,這表明MLA確實可以在內存效率與建模能力之間取得更好的平衡。
有趣的是,MLA的建模能力甚至超過了原始MHA。
 更具體地說,下表顯示了MHA、GQA和MQA在7B模型上的性能,其中MHA的性能明顯優於MQA和GQA。
更具體地說,下表顯示了MHA、GQA和MQA在7B模型上的性能,其中MHA的性能明顯優於MQA和GQA。
 [3]的作者還對MHA與MLA進行了分析,結果總結在下表中,其中MLA總體上取得了更好的結果。
[3]的作者還對MHA與MLA進行了分析,結果總結在下表中,其中MLA總體上取得了更好的結果。
 參考文獻
參考文獻
- [1] DeepSeek
- [2] DeepSeek-V3技術報告
- [3] DeepSeek-V2:一個強大、經濟高效的混合專家語言模型
- [4] DeepSeekMoE:邁向混合專家語言模型中最終的專家專業化
- [5] 混合專家模型的無輔助損失負載均衡策略
- [6] Attention Is All You Need
- [7] 通過總結長序列生成維基百科
- [8] 通過生成式預訓練改進語言理解
- [9] 快速Transformer解碼:一個寫頭就足夠了
- [10] GQA:從多頭檢查點訓練廣義多查詢Transformer模型
- [11] RoFormer:具有旋轉位置嵌入的增強型Transformer
以上是DeepSeek-V3解釋了1:多頭潛在註意力的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 我嘗試了使用光標AI編碼的Vibe編碼,這太神奇了!
Mar 20, 2025 pm 03:34 PM
我嘗試了使用光標AI編碼的Vibe編碼,這太神奇了!
Mar 20, 2025 pm 03:34 PM
Vibe編碼通過讓我們使用自然語言而不是無盡的代碼行創建應用程序來重塑軟件開發的世界。受Andrej Karpathy等有遠見的人的啟發,這種創新的方法使Dev
 如何使用DALL-E 3:技巧,示例和功能
Mar 09, 2025 pm 01:00 PM
如何使用DALL-E 3:技巧,示例和功能
Mar 09, 2025 pm 01:00 PM
DALL-E 3:生成的AI圖像創建工俱生成的AI正在革新內容創建,而OpenAI最新的圖像生成模型Dall-E 3處於最前沿。它於2023年10月發行,建立在其前任Dall-E和Dall-E 2上
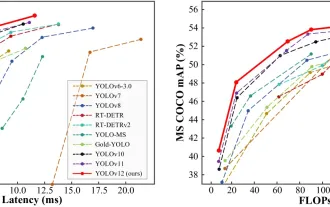 如何使用Yolo V12進行對象檢測?
Mar 22, 2025 am 11:07 AM
如何使用Yolo V12進行對象檢測?
Mar 22, 2025 am 11:07 AM
Yolo(您只看一次)一直是領先的實時對象檢測框架,每次迭代都在以前的版本上改善。最新版本Yolo V12引入了進步,可顯著提高準確性
 2025年2月的Genai推出前5名:GPT-4.5,Grok-3等!
Mar 22, 2025 am 10:58 AM
2025年2月的Genai推出前5名:GPT-4.5,Grok-3等!
Mar 22, 2025 am 10:58 AM
2025年2月,Generative AI又是一個改變遊戲規則的月份,為我們帶來了一些最令人期待的模型升級和開創性的新功能。從Xai的Grok 3和Anthropic的Claude 3.7十四行詩到Openai的G
 Elon Musk&Sam Altman衝突超過5000億美元的星際之門項目
Mar 08, 2025 am 11:15 AM
Elon Musk&Sam Altman衝突超過5000億美元的星際之門項目
Mar 08, 2025 am 11:15 AM
這項耗資5000億美元的星際之門AI項目由OpenAI,Softbank,Oracle和Nvidia等科技巨頭支持,並得到美國政府的支持,旨在鞏固美國AI的領導力。 這項雄心勃勃
 Sora vs veo 2:哪個創建更現實的視頻?
Mar 10, 2025 pm 12:22 PM
Sora vs veo 2:哪個創建更現實的視頻?
Mar 10, 2025 pm 12:22 PM
Google的VEO 2和Openai的Sora:哪個AI視頻發電機佔據了至尊? 這兩個平台都產生了令人印象深刻的AI視頻,但它們的優勢在於不同的領域。 使用各種提示,這種比較揭示了哪種工具最適合您的需求。 t
 Google的Gencast:Gencast Mini Demo的天氣預報
Mar 16, 2025 pm 01:46 PM
Google的Gencast:Gencast Mini Demo的天氣預報
Mar 16, 2025 pm 01:46 PM
Google DeepMind的Gencast:天氣預報的革命性AI 天氣預報經歷了巨大的轉變,從基本觀察到復雜的AI驅動預測。 Google DeepMind的Gencast,開創性
 哪個AI比Chatgpt更好?
Mar 18, 2025 pm 06:05 PM
哪個AI比Chatgpt更好?
Mar 18, 2025 pm 06:05 PM
本文討論了AI模型超過Chatgpt,例如Lamda,Llama和Grok,突出了它們在準確性,理解和行業影響方面的優勢。(159個字符)





 參考文獻
參考文獻

