二元搜尋樹是一種資料結構,它允許我們在短時間內保留數字的排序清單。它也被稱為二元樹,因為每個樹節點只能有兩個兄弟節點。二元搜尋樹可用於搜尋數字是否存在;它被稱為搜尋樹。運行時間複雜度為O(log(n))時間;二元搜尋樹與基本二元樹的差異如下 –
開始您的免費軟體開發課程
網頁開發、程式語言、軟體測試及其他
1.左子樹的節點都小於根節點。
2.右子樹的節點都比根節點大
3.子樹的每個節點同樣都是 BST,這意味著它們具有與節點本身相同的兩個品質。
1.設指定數組為:
給定數組:[8, 6, 2, 7, 9, 12, 4, 10]
2.讓我們從頂部元素 43 開始。插入 43 作為樹的根。
3.如果下一個元素小於根節點元素,則應將其插入為左子樹的根。
4.如果不是,則應插入為右子樹的根。
下圖描述了使用提供的元素建立二元搜尋樹的過程。
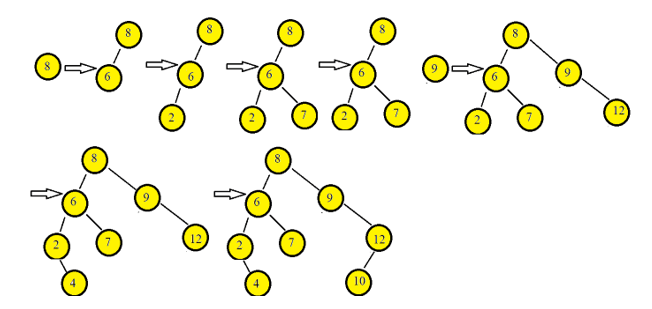
二分搜尋樹操作:
Java中二元搜尋樹支援的操作如下表所示 –
1. BST 搜尋 – 在二元搜尋樹中,找出某個元素的位置。
2. BST 中的插入 – 在二元搜尋樹的適當位置新增元素可確保二元搜尋樹屬性不會被破壞。
3. BST 中的刪除 – 刪除二元搜尋樹中的特定節點。但是,根據節點擁有的子節點數量,可能會出現多種刪除場景。
Java 中二元搜尋樹的範例,對二元搜尋樹執行操作 –
//程式可以在Eclipse IDE、JAVA 11中測試
package jex;
import java.util.Scanner;
class binarySearchTree {
//node class that defines BST node
class Node {
int key;
Node left, right;
public Node(int data){
key = data;
left = right = null;
}
}
// binary search tree root node
Node root;
// Constructor for binary search tree, first empty tree
binarySearchTree(){
root = null;
}
//delete a node from binary search tree
void deleteKey(int key) {
root = delete(root, key);
}
//recursive delete function
Node delete(Node root, int key) {
// if tree is empty
if (root == null) return root;
//traverse the tree
if (key < root.key)
//traverse left subtree
root.left = delete(root.left, key);
else if (key > root.key)
//traverse right subtree
root.right = delete(root.right, key);
else {
// if node having only one child
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// if node has two children;
root.key = minKey(root.right);
// removing the inorder sibling
root.right = delete(root.right, root.key);
}
return root;
}
int minKey(Node root) {
// initially min is root
int min = root.key;
// find minimum value
while (root.left != null) {
min = root.left.key;
root = root.left;
}
return min;
}
// insert a node in binary search tree
void insertKey(int key) {
root = insert(root, key);
}
// recursively insert a node
Node insert(Node root, int key) {
// initially, tree is empty
if (root == null) {
root = new Node(key);
return root;
}
// traverse the tree
if (key<root.key)
//insert in the left subtree
root.left = insert(root.left, key);
else if (key > root.key)
//insert in the right subtree
root.right = insert(root.right, key);
// return
return root;
}
// function to travel inorder of binary search tree
void inorder() {
inorder(root);
}
// recursively traverse the binary search tree
void inorder(Node root) {
if (root != null) {
inorder(root.left);
System.out.print(root.key + " ");
inorder(root.right);
}
}
boolean searchKey(int key) {
root = search(root, key);
if (root!= null)
return true;
else
return false;
}
//recursive insert function
Node search(Node root, int key) {
// If root is null or key is present at root
if (root==null || root.key==key)
return root;
// when val is greater than root's key
if (root.key > key)
return search(root.left, key);
// when val is lesser than root's key
return search(root.right, key);
}
}
public class client{
public static void main(String[] args) {
binarySearchTree t = new binarySearchTree();
// inserting 8, 6, 2, 7, 9, 12, 4, 10 data into the binary search tree
t.insertKey(8);
t.insertKey(6);
t.insertKey(2);
t.insertKey(7);
t.insertKey(9);
t.insertKey(12);
t.insertKey(4);
t.insertKey(10);
//print the binary search tree
System.out.println( "The binary search tree created with the input data :");
t.inorder();
//delete the leaf node
System.out.println( "\nThe binary search tree after deleting 4 leaf node :");
t.deleteKey(4);
t.inorder();
//delete the node with one child
System.out.println( "\nThe binary search tree after Delete 12 node with 1 child is :");
t.deleteKey(12);
t.inorder();
//search a key in the binary search tree
boolean res = t.searchKey (9);
System.out.println( "\n The node 9 found in binary search tree is :" + res );
res = t.searchKey (12);
System.out.println( "\n The node 10 found in binary search tree is :" + res );
}
}輸出:
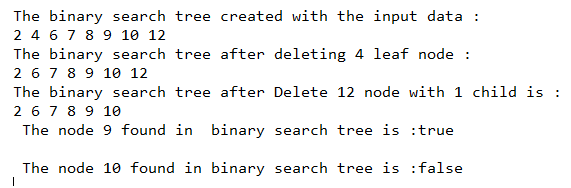
如上面的程序,創建了binarySearchTree類,它包含另一個內部類別Node,也包含建構子和方法。類別中定義的方法有deleteKey()、delete()、minKey()、insertKey()、insert()、inorder()、searchKey()和search()來執行具體操作。在 main 函數中,建立了 binarySearchTree 類別對象,向其中插入一些元素,然後在其物件上呼叫二元搜尋樹類別的方法,如上面的輸出所示。
二元搜尋樹也稱為二元樹,因為每個樹節點只能有兩個兄弟節點。二元搜尋樹是一種資料結構,可以在短時間內保留數字的排序清單。二元查找樹可以進行的操作:遍歷、插入、刪除、尋找。
以上是Java 中的二元搜尋樹的詳細內容。更多資訊請關注PHP中文網其他相關文章!




