有向無環圖中節點的所有祖先

2192。有向無環圖中某個節點的所有祖先

中

給你一個正整數n，表示有向無環圖（DAG）的節點數。節點編號從 0 到 n - 1（含）。

還給你一個 2D 整數數組邊，其中 Edges[i] = [from_i, to_i] 表示圖中存在一條從 fromi到 to_i的_邊。返回列表答案，其中answer[i]是第i

第

節點的祖先列表，按^升序排序。如果 u 可以透過一組邊到達 v，則節點 u 是另一個節點 v 的

祖先

。

範例1：

輸入：
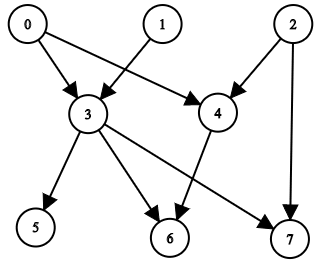
• n = 8，edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3, 6],[3,7],[4,6]]
輸出：
• [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1 ,2,3]]
說明：
• 上圖表示輸入圖。節點 0、1 和 2 沒有任何祖先。
  • 節點 3 有兩個祖先 0 和 1。
  • 節點 4 有兩個祖先 0 和 2。
  • 節點 5 有三個祖先 0、1 和 3。
  • 節點 6 有 5 個祖先：0、1、2、3 和 4。
  • 節點 7 有四個祖先 0、1、2 和 3。

範例2：

輸入：
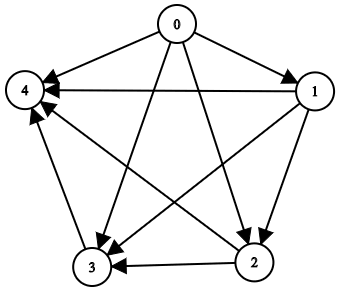
• n = 5，edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1, 4],[2,3],[2,4],[3,4]]
輸出：
• [[],[0],[0,1],[0,1,2],[0,1,2,3]]
說明：
• 上圖表示輸入圖。節點 0 沒有任何祖先。
  • 節點 1 有一個祖先 0.
  • 節點 2 有兩個祖先 0 和 1。
  • 節點 3 有三個祖先 0、1 和 2。
  • 節點 4 有四個祖先 0、1、2 和 3。

限制：

1

0

edges[i].length == 2

0 i

，到_i從

i

！ =到_i沒有重複的邊。

該圖是

有向

和無環。

解決方案：

雷雷

聯絡連結

領英
GitHub

以上是有向無環圖中節點的所有祖先的詳細內容。更多資訊請關注PHP中文網其他相關文章！