Format data adalah seperti berikut:
[
{
"event": {
"id": "2013",
"startTime": "00:57:00",
"endTime": "07:56:00",
"title": "list 1",
"backgroundColor": "#f6c79f",
"textColor": "#8c725b",
"order": 2014
}
},
{
"event": {
"id": "2016",
"startTime": "00:51:59",
"endTime": "06:57:00",
"title": "list 2",
"backgroundColor": "#a7bff7",
"textColor": "#5f6d8c",
"order": 2017
}
},
{
"event": {
"id": "2019",
"startTime": "00:11:00",
"endTime": "11:35:00",
"title": "list 3",
"backgroundColor": "#beea91",
"textColor": "#728c57",
"order": 2020
}
},
{
"event": {
"id": "2022",
"startTime": "09:01:00",
"endTime": "13:18:00",
"title": "list 4",
"backgroundColor": "#d1b1ff",
"textColor": "#73618c",
"order": 2023
}
}
]Penerangan keperluan:
Plot setiap data pada peta koordinat 1 hari (00:00 - 24:00),
Rajah yang mungkin adalah seperti berikut: 
1 Menurut startTime和endTime data, koordinat data pada paksi Y boleh diperolehi ( dinyatakan sebagai nilai atas dan ketinggian, dilaksanakan )
2 Memandangkan setiap tempoh masa mungkin bersilang (sebahagian daripada tempoh masa (startTime - endTime) satu peristiwa berada dalam tempoh masa peristiwa lain, ia dipanggil persimpangan), maka peristiwa yang bersilang pada X 轴上相交的事件平分X轴的宽度(表现为left和width值)
2.1.如果一个事件没有与任何事件相交,则这个事件的宽度是100%
2.2 如果相交平分的话,必须order2.3 Sesuatu peristiwa mungkin bersilang dengan acara lain, atau mungkin bersilang dengan beberapa acara lain
Soalan saya ialah bagaimana untuk melaksanakan algoritma membahagi dua lebar paksi-X dan meletakkan kedudukan kiri? Iaitu, kiri dan lebar setiap elemen bernilai algoritma
Kandungan tambahan: A dan B bersilang, B dan C bersilang, dan A dan C tidak bersilang, maka ABC juga dibahagikan sama banyak
Ditulis secara kasar, idea asasnya ialah
Isih dahulu semua tugasan dari besar ke kecil (bahagian ini ditiadakan)
Tekan hujung mula untuk menjana objek tugasan, dan gunakan add_one daripada objek rajah untuk menambahkannya pada rajah secara bergilir-gilir.
Apabila memasukkan objek, tentukan objek bertindih antara objek sedia ada, jadikan kirinya sama dengan kiri+1 objek bertindih terbesar, dan kemas kini lebar maksimum
Akhir sekali, gunakan kaedah is_overlap untuk mengesan acara dalam tugasan yang tidak bersilang dengan sebarang acara dan menandakannya di sebelah kiri acara ini ditetapkan kepada 0 dan lebar ditetapkan kepada 100%. selain daripada peristiwa ini, lebar ditetapkan ialah 1/max_width, kiri ditetapkan kepada 1/max_width*(kiri-1) (bahagian ini diabaikan)
Kod berikut ialah langkah 2 dan 3
Perkumpulan 2D
Kumpulan pertama secara menegak (VGroups). Peristiwa yang mempunyai perhubungan yang bersilang dikumpulkan ke dalam kumpulan yang sama. Setiap kumpulan adalah bebas (kumpulan tidak bersilang). Algoritma pengelompokan ialah: layan setiap peristiwa sebagai nod, dan jika dua nod bersilang, satu tepi disambungkan. Dengan cara ini, graf diperoleh, dan pengelompokan adalah untuk mencari komponen bersambung graf ini. Anda boleh menggunakan algoritma seperti carian mendalam-dahulu atau carian luas-dahulu untuk mencari komponen yang disambungkan.
VGroups)。凡之间有相交关系的事件分入同一组。各组之间是独立的(组间不相交)。分组算法是:将每个事件看做节点,若两个节点相交,则连一条边。这样得到一个图,分组即求此图的连通分量。可以用深度优先搜索或者广度优先搜索等算法求连通分量。纵向组内再横向分组(
Kumpulkan secara mendatar dalam kumpulan menegak (HGroupsDengan cara ini, selepas mengumpulkan dua dimensi secara menegak dan mendatar, adalah mudah untuk menukarnya kepada grafik.
Ujian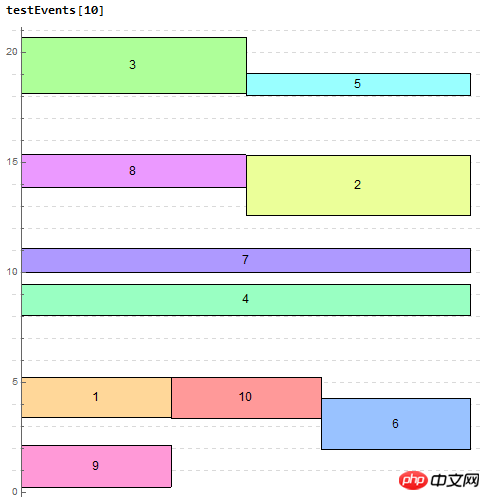
Dilampirkan:
Mahematica🎜 kod🎜@saigyouyou
Mungkin begini