
Pengarang |. Wang Hao
Pengulas | Python/Rust/Go Tunggu sebentar Kelahiran siri bahasa pengaturcaraan baharu dan perkembangan pesat teknologi pencarian maklumat juga menjadi sorotan. Model perniagaan teknologi tulen pertama di Internet ialah teknologi enjin carian yang diwakili oleh Google dan Baidu. Walau bagaimanapun, apa yang tidak dijangkakan oleh semua orang ialah sistem pengesyoran itu telah lama wujud. Seawal
1992 , sistem pengesyoran pertama dalam sejarah manusia diterbitkan dalam bentuk makalah Pada masa ini, Google dan Baidu masih belum lahir. tidak dianggap sebagai keperluan tegar seperti enjin carian, dan banyak unicorn tidak lama lagi dilahirkan. Syarikat teknologi dengan sistem pengesyoran sebagai teknologi teras mereka tidak akan muncul sehingga kebangkitan Toutiao dan Douyin dalam era 2010 . Tidak dinafikan bahawa Toutiao dan Douyin telah menjadi syarikat perwakilan yang paling berjaya dalam sistem pengesyoran. Jika enjin carian teknologi perolehan maklumat generasi pertama telah didahulukan oleh orang Amerika, maka sistem pengesyoran teknologi perolehan maklumat generasi kedua dikawal ketat oleh orang Cina. Dan kini kita menghadapi generasi ketiga teknologi perolehan maklumat
—— perolehan maklumat berdasarkan model bahasa yang besar. Pada masa ini, penggerak pertama adalah negara Eropah dan Amerika, tetapi China dan Amerika Syarikat sedang bergerak ke hadapan bersama-sama.
perolehan maklumat berdasarkan model bahasa yang besar. Pada masa ini, penggerak pertama adalah negara Eropah dan Amerika, tetapi China dan Amerika Syarikat sedang bergerak ke hadapan bersama-sama.
Dalam beberapa tahun kebelakangan ini, persidangan berwibawa dalam bidang sistem pengesyoran RecSys kerap menganugerahkan anugerah kertas terbaik kepada Syor Berurutan)
(Syor) . Ini menunjukkan bahawa medan ini semakin memberi perhatian kepada aplikasi menegak. Terdapat aplikasi menegak sistem pengesyoran yang begitu penting, tetapi ia belum membuat gelombang besar setakat ini Medan ini adalah pengesyoran berasaskan senario (Pengesyoran yang menyedari konteks), dirujuk sebagai KERETA. Kami kadang-kadang melihat beberapa Bengkel dari KERETA , tetapi Bengkel ini tidak menghasilkan lebih daripada 10 , iaitu jumlah yang sangat kecil setiap tahun. KERETA Ia boleh digunakan untuk apa? Pertama sekali CARS sudah pun digunakan oleh syarikat makanan segera seperti Burger King. Ia juga boleh mengesyorkan muzik kepada pengguna berdasarkan adegan semasa pengguna memandu kereta. Di samping itu, kita boleh memikirkannya, adakah mungkin untuk kita mengesyorkan rancangan perjalanan kepada pengguna berdasarkan keadaan cuaca? Atau mengesyorkan makanan kepada pengguna berdasarkan keadaan fizikal mereka? Malah, selagi kita memberikan permainan penuh kepada imaginasi kita, kita sentiasa boleh mencari aplikasi praktikal yang berbeza untuk KERETA .
Namun, persoalan timbul, memandangkan KERETA digunakan secara meluas, mengapa begitu sedikit orang yang menerbitkan kertas kerja? Alasannya mudah, kerana hampir tiada set data awam tersedia untuk KERETA . Pada masa ini, set data awam terbaik CARS
ialah set data LDOS-CoMoDa dari Slovenia. Selain daripada ini, sukar untuk mencari set data lain. LDOS-CoMoDa menyediakan data pemandangan pengguna semasa menonton filem dalam bentuk tinjauan, membolehkan penyelidik melibatkan diri dalam penyelidikan CARS . Titik masa pendedahan data adalah sekitar 2012 hingga 2013 , tetapi pada masa ini sangat sedikit orang yang mengetahui tentang pengumpulan data ini. Kembali kepada perniagaan, artikel ini terutamanya memperkenalkan algoritma MatMat / MovieMat dan algoritma PowerMat . Algoritma ini ialah alat yang berkuasa untuk menyelesaikan masalah KERETA
. Mari kita lihat dahulu bagaimana MatMat mentakrifkan masalah CARS : Kami mula-mula mentakrifkan semula matriks penilaian pengguna, dan kami menggantikan setiap nilai rating matriks penilaian pengguna dengan matriks segi empat sama. Unsur pepenjuru bagi matriks segi empat sama ialah nilai skor asal, dan unsur luar pepenjuru ialah maklumat pemandangan. Kami mentakrifkan di bawah fungsi kehilangan algoritma MatMat , yang mengubah suai fungsi kehilangan penguraian matriks klasik dan mempunyai bentuk berikut:
di mana U dan V adalah kedua-dua matriks. Dengan cara ini, kami menukar produk titik vektor dalam pemfaktoran matriks asal. Tukar pendaraban titik vektor kepada pendaraban matriks. Mari kita ambil contoh berikut:

Kami melakukan eksperimen perbandingan prestasi pada MovieLens Small Dataset dan mendapat keputusan berikut:
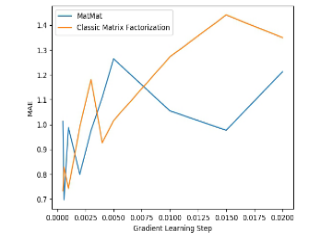
boleh lihat anda
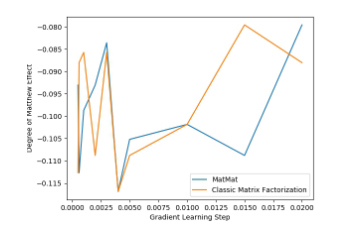
Kesan algoritma adalah lebih baik daripada algoritma penguraian matriks klasik. Mari kita semak semula kesaksamaan sistem pengesyoran: Ini dapat dilihat bahawa MatMat masih menunjukkan prestasi yang baik dari segi penunjuk keadilan. Proses penyelesaian MatMat agak rumit Malah penulis yang mencipta algoritma tidak menulis proses derivasi dalam kertas. Tetapi seperti kata pepatah, jika anda belajar algebra linear dengan baik, anda tidak akan takut mengembara ke seluruh dunia. Saya percaya bahawa pembaca pintar akan dapat menyimpulkan formula yang berkaitan dan melaksanakan algoritma ini. MatMat Alamat asal kertas algoritma boleh didapati di pautan berikut: //m.sbmmt.com/link/9b8c60725a0193e78368bf8b84c37fb2🜎 Kertas kerja ini ialah Anugerah Laporan Kertas Terbaik Persidangan Akademik Antarabangsa IEEE ICISCAE 2021
. AlgoritmaMatMat digunakan dalam bidang pengesyoran filem berasaskan adegan Contoh filem algoritma ini dinamakan MovieMat. Matriks penarafan MovieMat
ditakrifkan seperti berikut: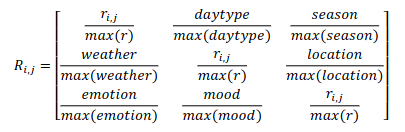
Pengarang kemudiannya menjalankan eksperimen perbandingan:
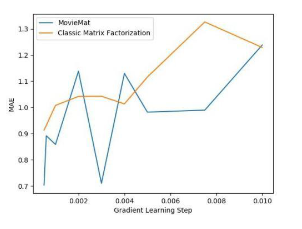
di 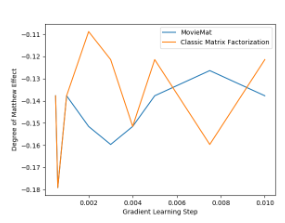
set data, MovieMat mencapai prestasi yang jauh lebih tinggi daripada penguraian matriks klasik. Mari kita lihat keputusan penilaian keadilan: Dari segi keadilan, penguraian matriks klasik telah mencapai keputusan yang lebih baik daripada MovieMat
. Kertas asal MovieMat boleh didapati di pautan berikut: //m.sbmmt.com/link/f4ec6380c50a68a7c35d109bec48aebf. Kita kadangkala menghadapi masalah sebegini. Apakah yang perlu kami lakukan apabila kami tiba di lokasi baharu dan hanya mempunyai data pemandangan tetapi tiada data penilaian pengguna? Tidak mengapa, Ratidar Technologies LLC (Beijing Daping Qizhi Network Technology Co., Ltd. ) mencipta algoritma CARS berdasarkan pembelajaran sifar-shot
Kertas asal PowerMat boleh didapati di pautan berikut: //m.sbmmt.com/link/1514f187930072575629709336826443 Pencipta
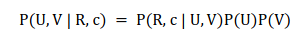 PowerMat
PowerMat
meminjam MAP dan DotMat dan mentakrifkan fungsi MAP berikut: MAP
di mana 🎜🎜U 🎜🎜 adalah pengguna vektor ciri, 🎜🎜V 🎜🎜 ialah vektor ciri item, 🎜🎜R 🎜🎜 ialah nilai penilaian pengguna dan 🎜🎜C 🎜🎜 ialah pembolehubah pemandangan. Secara khusus, kami mendapat formula berikut: 🎜🎜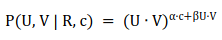
Menggunakan turunan kecerunan stokastik untuk menyelesaikan masalah ini, kami mendapat formula berikut:
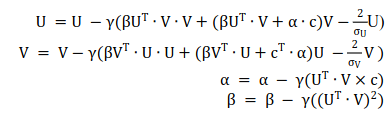
Melalui pemerhatian, kami mendapati tiada pembolehubah berkaitan data input dalam set formula ini, jadi PowerMat ialah algoritma pembelajaran sifar pukulan yang berkaitan hanya dengan senario. Algoritma ini boleh digunakan dalam senario berikut: pelancong merancang untuk pergi ke tempat tertentu, tetapi tidak pernah ke sana, jadi mereka hanya mempunyai data pemandangan seperti cuaca Kami boleh menggunakan PowerMat untuk mengesyorkan tarikan daftar masuk kepada. pelancong, dsb.
Berikut ialah data perbandingan antara PowerMat dan algoritma lain:

Melalui gambar ini, kita dapati MoviePower bendera Gendangnya agak, bukan Mereka setanding, dan hasilnya lebih baik daripada algoritma penguraian matriks klasik. Gambar di bawah menunjukkan bahawa walaupun dari segi keadilan indeks , PowerMat masih menunjukkan prestasi yang kukuh:
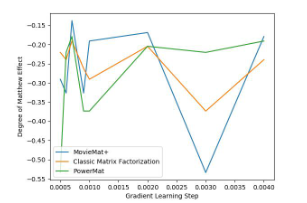
Melalui percubaan 🜜 yang sangat baik KERETA algoritma. Jurutera data internet sering mengatakan bahawa data adalah di atas segalanya. Dan sekitar era 2010
, terdapat aliran yang kukuh di Internet yang menaik pada data dan menurun pada algoritma. KERETA adalah contoh yang bagus. Oleh kerana sebahagian besar orang tidak mempunyai akses kepada data yang berkaitan, pembangunan bidang ini telah sangat terhad. Terima kasih kepada penyelidik Slovenia kerana membuat pengumpulan data LDOS-CoMoDa kepada umum, kami berpeluang untuk membangunkan bidang ini. Kami juga berharap semakin ramai yang mengambil berat tentang kereta, mendarat kereta, dan membiayai kereta ...
🎗 Funplus Ketua Makmal Kepintaran Buatan. Beliau telah memegang jawatan eksekutif teknologi dan teknologi di ThoughtWorks, Douban, Baidu, Sina dan syarikat lain. Setelah bekerja di syarikat Internet, teknologi kewangan, permainan dan syarikat lain selama
Atas ialah kandungan terperinci Belajar algebra linear dengan baik dan bermain dengan sistem pengesyoran. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Aplikasi kecerdasan buatan dalam kehidupan
Aplikasi kecerdasan buatan dalam kehidupan
 Douyin tidak boleh memuat turun dan menyimpan video
Douyin tidak boleh memuat turun dan menyimpan video
 Cara menonton rekod main balik siaran langsung di Douyin
Cara menonton rekod main balik siaran langsung di Douyin
 Semak status dalam talian rakan di TikTok
Semak status dalam talian rakan di TikTok
 Apa masalah Douyin terhempas?
Apa masalah Douyin terhempas?
 Apakah konsep asas kecerdasan buatan
Apakah konsep asas kecerdasan buatan
 Apakah itu blockchain web3.0
Apakah itu blockchain web3.0
 Apakah maksud STO dalam blockchain?
Apakah maksud STO dalam blockchain?




