Kaedah pelaksanaan Matlab dan paparan grafik penyelesaian berangka dan analisis kepada masalah nilai awal persamaan pembezaan dalam selang waktu

Gunakan matlab untuk menyelesaikan masalah nilai awal persamaan pembezaan Penyelesaian berangka dan julat penyelesaian analitik adalah selang dan dilukis

Gunakan matlab untuk menyelesaikan persamaan pembezaan 5261 penyelesaian berangka 4102 masalah nilai awal dan penyelesaian analitik, anda boleh mengendalikannya seperti ini:

1. Penyelesaian berangka

Penyelesaian berangka kepada masalah nilai awal bagi persamaan pembezaan boleh diselesaikan menggunakan fungsi oda.

Pertama, sesuaikan fungsi persamaan pembezaan, iaitu

dy = 3/x*y+x^3*(exp(x)+cos(x))-2*x;

Kedua, tentukan syarat awal iaitu

y0=[(exp(pi)+2/pi)*pi^3];

Ketiga, gunakan fungsi ode45 untuk mencari penyelesaian berangkanya [x, y]

2. Penyelesaian analitikal

Penyelesaian analitikal kepada masalah nilai awal bagi persamaan pembezaan boleh diselesaikan menggunakan fungsi dsolve.

Mula-mula, isytiharkan pembolehubah untuk y(x), iaitu

syms y(x)

Kedua, terbitan pertama y(x), iaitu

Dy=diff(y,1)

Ketiga, gunakan fungsi dsolve untuk mencari ungkapan penyelesaian analitiknya y(x)

y=dsolve(Dy==3/x*y+x^3*(exp(x)+cos(x))-2*x,y(pi)==(exp(pi)+2/pi) *pi^3)

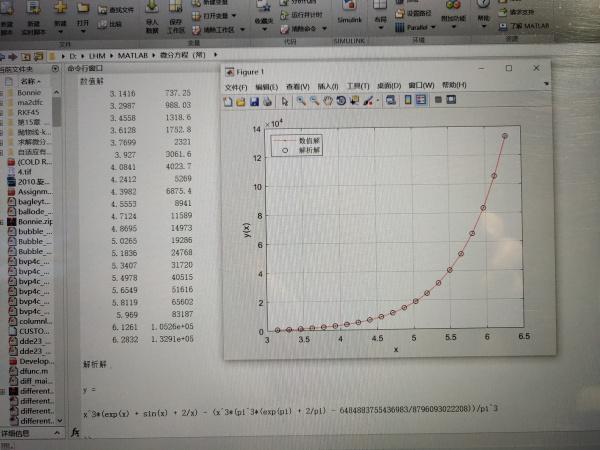
3. Lukiskan penyelesaian berangka dan lengkung penyelesaian analitik

Pertama, gunakan fungsi plot untuk melukis lengkung penyelesaian berangka

plot(x.y)

Kedua, hitung nilai y yang bersamaan dengan y untuk satu siri nilai x dalam selang [π, 2π]

Ketiga, gunakan fungsi plot untuk melukis lengkung penyelesaian analitik

Selepas menjalankan kod, anda boleh mendapatkan hasil berikut.

masalah matlab

%%%%%%%%%%%%%%%%%%% program sumber

i=0;equ=0;jumlah=0;

data=input('sila masukkan nombor: ');

sementara(data~=0)

jumlah=jumlah+data;

key=input('sila teruskan: ');

data=kunci;

i=i+1;

akhir

equ=jumlah/i;

equ,sum

%%%%%%%%%%%%%%%%%%%%%%%%%

Hasil pelaksanaan:

sila masukkan nombor: 1

sila teruskan: 2

sila teruskan: 3

sila teruskan: 4

sila teruskan: 5

sila teruskan: 0

equ =

3

jumlah =

15

Atas ialah kandungan terperinci Kaedah pelaksanaan Matlab dan paparan grafik penyelesaian berangka dan analisis kepada masalah nilai awal persamaan pembezaan dalam selang waktu. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!