Penjelasan terperinci tentang kaedah pelaksanaan kaedah lelaran bagi persamaan tak linear dalam matlab

Penerangan terperinci pelaksanaan matlab bagi kaedah lelaran sistem persamaan tak linear

Kaedah lelaran Newton:

fungsi[x0,n]=newton(fx,dfx,x0,tol,N)

% kaedah lelaran Newton

% Parameter pertama fx ialah ungkapan fungsi yang diingini tentang pembolehubah x.

% Parameter kedua dfx ialah terbitan pertama fx.

% x0 ialah nilai awal lelaran.

% tol ialah had ralat lelaran.

% N Bilangan lelaran maksimum.

x=x0;f0=eval(fx);df0=eval(dfx);

n=0;

disp('[ n xn xn+1 delta ]');

sementara n

x1=x0-f0/df0;

x=x1;f1=eval(fx);df1=eval(dfx);

delta=abs(x0-x1);

% X=[n,x0,x1,delta];

disp(X); % digunakan untuk memaparkan keputusan pertengahan

jika delta

fprintf('Pengiraan lelaran berjaya')

kembali

lain

n=n+1;

x0=x1;f0=f1;df0=df1;

akhir

akhir

jika n==N+1

fprintf('Pengiraan lelaran gagal')

akhir

Dua lagi boleh diubah suai sedikit berdasarkan ini.

Atur cara MATLAB untuk menggunakan lelaran Newton untuk menyelesaikan persamaan tak linear

Berikan anda versi penuh:

% kaedah Newton untuk menyelesaikan persamaan tak linear

fungsi utama()

clc; kosongkan semua;

f = @(x)log(x+sin(x)); % fungsi ujian

df = @(x)(1+cos(x))/(x+sin(x)); % fungsi terbitan

x0 = 0.1; % nilai awal lelaran

x = TestNewton(f, df, x0) % kaedah Newton

fungsi x = TestNewton(fname, dfname, x0, e, N)

% Tujuan: Kaedah lelaran Newton untuk menyelesaikan persamaan tak linear f(x)=0

% fname dan dfname masing-masing mewakili pemegang fungsi M atau ungkapan fungsi terbenam bagi f(x) dan fungsi terbitannya

% x0 ialah nilai awal lelaran, e ialah ketepatan (nilai lalai 1e-7)

% x mengembalikan penyelesaian berangka dan memaparkan proses pengiraan Tetapkan had atas bilangan lelaran N untuk mengelakkan perbezaan (lalai 500 kali)

.

% parameter input

jika nargin

N = 500;

akhir

jika nargin

e = 1e-7;

akhir

x = x0; % nilai awal

x0 = x+2*e; % terapung

k = 0; % bilangan langkah

fprintf('x[%d]=%12.9fn', k, x) % maklumat cetakan

sementara abs(x0-x)>e & k

k = k+1; % rekod bilangan langkah

x0 = x; % kemas kini x(k)

x = x0 - feval(fname,x0)/feval(dfname,x0); % kemas kini x(k+1)

fprintf('x[%d]=%12.9fn', k, x) % maklumat cetakan

akhir

jika k == N

fprintf('Bilangan maksimum lelaran telah dicapai'); % lelaran tamat

akhir

Hasil:

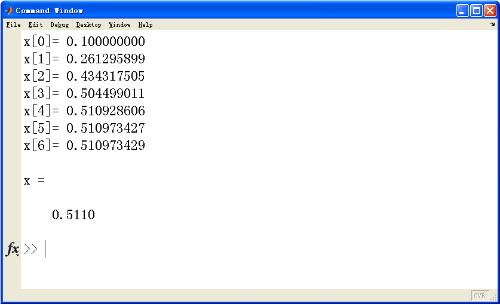
Atas ialah kandungan terperinci Penjelasan terperinci tentang kaedah pelaksanaan kaedah lelaran bagi persamaan tak linear dalam matlab. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!