
(1) Formula analisis ialah integer, dan pembolehubah bebas boleh menjadi sebarang nombor nyata
Untuk pecahan dalam ungkapan analitikal, pembolehubah tidak bersandar harus mengambil nilai nyata bukan sifar.
(3). Bagi kes di mana ungkapan analitik ialah radikal kuadratik atau radikal genap, kita perlu mengambil pembolehubah bebas sebagai nombor nyata yang radicandnya tidak kurang daripada 0. Ini memastikan bahawa ungkapan analitik adalah bermakna dan boleh diselesaikan.
(4). Untuk fungsi komposit dengan ungkapan analitikal berfungsi yang kompleks, pertimbangan menyeluruh harus diberikan untuk memastikan setiap elemen dalam ungkapan analitikal adalah bermakna. Sebelum melakukan pengiraan, kita perlu menganalisis domain dan julat nilai dengan teliti bagi setiap fungsi untuk memastikan ungkapan analitik bagi keseluruhan fungsi komposit adalah bermakna. Ini mengelakkan ralat atau ketidakpastian semasa pengiraan.
Apabila menyelesaikan persamaan seperti y=1/x+√(3x-1), kita perlu mempertimbangkan maksud sebenar fungsi dan menentukan julat nilai pembolehubah bebas. Untuk persamaan ini, julat nilai pembolehubah tidak bersandarnya x harus memenuhi x ≥ 1/3.2 untuk memastikan fungsi itu bermakna dalam erti kata yang praktikal. Dengan cara ini kita boleh menyelesaikan masalah dengan lebih baik dan mendapat hasil yang betul.
Pembolehubah fungsi adalah serupa dengan pembolehubah lain seperti integer Ia tidak mempunyai makna praktikal dan hanya digunakan untuk menggantikan sasaran. Pembolehubah fungsi termasuk pembolehubah bebas dan pembolehubah bersandar. Pembolehubah bebas ialah pembolehubah yang mengambil sebarang nilai dalam julat nilai tertentu (domain), manakala pembolehubah bersandar ialah pembolehubah yang diperoleh selepas pembolehubah bebas mengambil nilai mengikut peraturan fungsi.
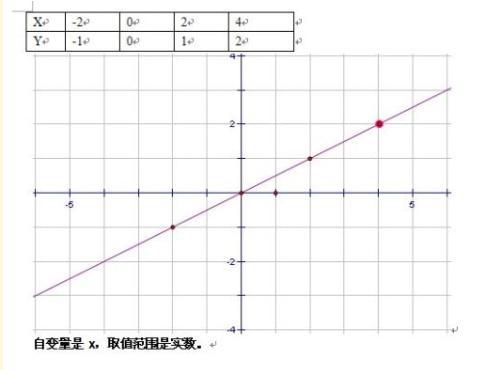
Maklumat lanjutan:
Julat nilai pembolehubah bebas merujuk kepada semua nilai pembolehubah bebas dalam fungsi yang menjadikannya bermakna. Dalam matematik, kami mentakrifkan julat nilai untuk hujah sesuatu fungsi untuk memastikan fungsi itu masuk akal dalam julat ini. Julat ini boleh menjadi set nombor nyata, integer, nombor rasional atau julat berangka khusus lain, bergantung pada takrifan dan keperluan fungsi.
Cara menentukan julat nilai pembolehubah bebas:
Pertama, kita perlu mempertimbangkan julat nilai pembolehubah bebas untuk memastikan bahawa ungkapan analitik adalah bermakna. Jika ungkapan analitik ialah integer, maka pembolehubah bebas boleh menjadi sebarang nombor nyata. Dan jika ungkapan analitik dalam bentuk pecahan, kita perlu memastikan bahawa penyebutnya bukan sifar, jadi julat nilai pembolehubah bebas adalah semua nombor nyata yang menjadikan penyebut bukan sifar. Dengan memilih julat nilai pembolehubah bebas secara munasabah, kita boleh memastikan kesahihan ungkapan analitikal.
Apabila terdapat punca kuasa dua dalam ungkapan analitik, anda perlu memastikan bahawa radicand tidak kurang daripada nombor sebenar sifar, supaya anda boleh mendapatkan penyelesaian yang sah. Apabila ungkapan analitikal berfungsi digunakan untuk mewakili masalah sebenar, nilai pembolehubah bebas mesti menjadikan masalah sebenar bermakna untuk memastikan rasional keputusan. Dengan cara ini, kita boleh menentukan julat nilai pembolehubah bebas berdasarkan dua prinsip ini untuk mendapatkan jawapan yang betul.
Julat nilai pembolehubah bebas boleh menjadi tidak terhingga, terhingga atau nombor tunggal (atau beberapa). Apabila terdapat berbilang ungkapan algebra dalam ungkapan analitik fungsi, julat nilai pembolehubah tidak bersandar bagi fungsi tersebut hendaklah bahagian biasa julat nilai pembolehubah bebas dalam setiap ungkapan algebra.
Pembolehubah fungsi dan masalah praktikal:
Dalam proses menyelesaikan masalah praktikal, kita sering menghadapi konsep pembolehubah dan pemalar. Pembolehubah dan pemalar selalunya relatif, dan identiti mereka boleh ditukar kepada satu sama lain dalam proses penyelidikan yang berbeza. Walau bagaimanapun, apabila menangani masalah praktikal, kita perlu memberi perhatian kepada membezakan antara pembolehubah dan pemalar. Pembolehubah boleh berubah, manakala pemalar tetap. Oleh itu, kita perlu menentukan masa untuk menggunakan pembolehubah dan pemalar berdasarkan kes demi kes dan menggunakannya secara fleksibel semasa proses penyelesaian teka-teki.
Seterusnya, kita boleh cuba mencari hubungan antara pembolehubah dan belajar cara menggunakan fungsi untuk mewakilinya. Dengan cara ini, kami lebih mampu menyelesaikan teka-teki dan mencari cara untuk melepasi tahap.
Apabila menyelesaikan masalah praktikal, adalah sangat penting untuk menggunakan graf fungsi. Kita perlu memahami dengan betul maksud paksi mendatar dan menegak, memahami sifat graf fungsi, dan dapat mengenal pasti dan menggunakan imej dengan tepat untuk menyelesaikan masalah. Melalui kaedah ini, kita dapat lebih memahami ciri dan tingkah laku fungsi, dan dengan itu menyelesaikan pelbagai masalah praktikal dengan lebih berkesan.
Rujukan: Ensiklopedia Sogou - Pembolehubah Fungsi
1. Gambaran keseluruhan kandungan:
1. Konsep berkaitan fungsi:
Secara amnya, kami akan melibatkan dua pembolehubah x dan y dalam proses perubahan tertentu. Jika bagi setiap nilai khusus x dalam julat tertentu, terdapat nilai y yang sepadan unik, maka kita katakan bahawa y ialah fungsi x, dan x dipanggil pembolehubah bebas.
Maksud fungsi perlu difahami dari aspek berikut:
Apabila kita mengkaji proses perubahan tertentu, kita meneroka hubungan fungsi antara dua pembolehubah. Dalam proses penyelidikan yang berbeza, pembolehubah dan pemalar boleh ditukar kepada satu sama lain, iaitu pemalar dan pembolehubah adalah relatif kepada proses tertentu. Fleksibiliti dalam penukaran bersama ini membolehkan kami memahami dan menganalisis dengan lebih baik hubungan antara pembolehubah.
(2) Julat nilai pembolehubah x terdiri daripada setiap nilai yang dibenarkan. (3) Terdapat padanan yang pasti antara pembolehubah x dan y, iaitu, bagi setiap nilai x yang dibenarkan, terdapat nilai y unik yang sepadan dengannya.
Cara memahami fungsi yang sama:
Konsep fungsi boleh difahami apabila terdapat korespondensi khas antara pembolehubah x dan pembolehubah y (iaitu peraturan yang sepadan), dan dalam julat nilai pembolehubah x, setiap nilai x sepadan dengan nilai y yang unik, maka pembolehubah y ialah fungsi pembolehubah x. Secara ringkasnya, konsep fungsi merangkumi dua perkara utama berikut:
(1) Hubungan fungsional antara y dan x;
(2) Julat nilai pembolehubah tidak bersandar x dalam hubungan berfungsi.Ini bermakna fungsi yang sama mesti memenuhi dua aspek di atas, iaitu, ungkapan hubungan fungsi adalah sama (atau sama selepas ubah bentuk), dan julat nilai pembolehubah bebas x juga sama bukan fungsi yang sama. Adalah lebih mudah untuk melihat sama ada ungkapan hubungan fungsian adalah sama atau tidak, dan julat nilai pembolehubah bebas x kadangkala mudah diabaikan. Sila beri perhatian kepada perkara ini.
Antara fungsi berikut, yang mempunyai hubungan fungsi yang sama seperti y=x ialah ( ).
Kaedah penyelesaian teka-teki: Pertama, kita perlu memudahkan ungkapan analitikal bagi empat fungsi dan membandingkannya dengan y=x untuk melihat sama ada ia adalah sama. Kemudian, kita perlu menentukan julat nilai pembolehubah bebas x dalam setiap fungsi dan membandingkannya dengan ungkapan analitikal y=x dan julat nilai pembolehubah bebas x. Ia adalah fungsi yang sama hanya jika kedua-dua syarat dipenuhi.
Penyelesaian: Fungsi y=x, julat nilai pembolehubah tidak bersandar x ialah semua nombor nyata.
, Julat nilai pembolehubah tidak bersandar x ialah semua nombor nyata x≥0.
, julat nilai pembolehubah tidak bersandar x ialah semua nombor nyata x≠0.
, julat nilai pembolehubah tidak bersandar x ialah semua nombor nyata.
, julat nilai pembolehubah tidak bersandar x ialah semua nombor nyata.
Jelas sekali, hanya formula analisis pilihan (C) mempunyai julat nilai yang sama seperti y=x, jadi jawapan yang betul hendaklah (C).
2. Julat nilai hujah fungsi
Prinsip julat nilai argumen fungsi ialah:
(1) Formula analisis ialah integer, dan pembolehubah bebas boleh mengambil sebarang nombor nyata.
Ungkapan analitik ialah pecahan, jadi apabila menentukan nilai pembolehubah tidak bersandar, anda perlu mengelak daripada membuat penyebut sama dengan sifar. Ini kerana penyebut sifar menyebabkan pecahan tidak boleh dikira. Pastikan penyebut bagi ungkapan analitik adalah bukan sifar untuk mendapatkan penyelesaian yang sah.
Untuk kes di mana ungkapan analisis tidak rasional, kita perlu memberi perhatian kepada dua perkara berikut: 1. Jika ia adalah radikal kuadratik, nilai radikal mestilah lebih besar daripada atau sama dengan sifar. Oleh itu, kita perlu mencari julat nilai pembolehubah bebas supaya modulus lebih besar daripada atau sama dengan sifar. 2. Jika ia adalah radikal padu, pembolehubah bebas boleh menjadi sebarang nombor nyata. Ini bermakna kita boleh memilih mana-mana nombor nyata sebagai nilai pembolehubah bebas. Pertimbangan ini akan membantu kami menghuraikan ungkapan tidak rasional dengan betul dan menentukan julat nilai untuk pembolehubah bebas.
Jika ungkapan analitik disintesis daripada bentuk di atas, maka julat nilai pembolehubah bebas perlu memenuhi syarat masing-masing pada masa yang sama. Dengan cara ini, kita dapat menyelesaikan masalah dengan lebih baik.
3. Nilai fungsi
Masalah yang berkaitan dengan nilai fungsi boleh diubah menjadi nilai ungkapan algebra.
4. Graf fungsi
Graf fungsi merealisasikan transformasi bersama antara nombor dan bentuk.
Atas ialah kandungan terperinci Bagaimana untuk menentukan julat nilai pembolehubah bebas dalam fungsi. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 tahap pengasingan transaksi lalai mysql
tahap pengasingan transaksi lalai mysql
 Kaedah pelaksanaan fungsi main balik dalam talian Python
Kaedah pelaksanaan fungsi main balik dalam talian Python
 securefx tidak boleh menyambung
securefx tidak boleh menyambung
 IIS penyelesaian ralat tidak dijangka 0x8ffe2740
IIS penyelesaian ralat tidak dijangka 0x8ffe2740
 Kedudukan terkini pertukaran mata wang digital
Kedudukan terkini pertukaran mata wang digital
 Apakah yang dimaksudkan untuk menyambung ke tingkap?
Apakah yang dimaksudkan untuk menyambung ke tingkap?
 penggunaan klonenod
penggunaan klonenod
 Tutorial penggunaan pelayan awan
Tutorial penggunaan pelayan awan




