
对于身处科研领域的人来说,或多或少的都听到过 P/NP 问题,该问题被克雷数学研究所收录在千禧年大奖难题中,里面有七大难题,大家熟知的庞加莱猜想、黎曼假设等都包含在内。而且这个组织还为能够攻克该问题的研究人员提供了上百万美元的奖金悬赏。
P/NP 问题最早在 1971 年由史提芬·库克(Stephen A. Cook)和列昂尼德·列文分别提出。多年来,许多人都投入到研究这个问题中。然而,有人表示解决 P=NP 问题可能需要保守估计还需要 100 年的时间
近年来,有一些人声称已经证明了 P 等于或者不等于 NP,但是这些证明过程都存在错误。然而,到目前为止,还没有人能够给出一个确切的答案
随着人工智能技术的发展,尤其是最近一年大型语言模型的快速更新,研究人员开始尝试利用人工智能技术来解决一些全球性难题
研究者们来自微软研究院、北京大学、北航等机构,他们提出使用大语言模型(LLM)来增强和加速对P versus NP问题的研究
本文提出了一个通用框架,即苏格拉底推理(Socratic reasoning),用于促使LLM进行深入思考并解决复杂问题。在这个框架的基础上,LLM能够递归地发现、解决和整合问题,同时还能进行自我评估和完善
本文对 P vs. NP 问题的试点研究表明,GPT-4 成功地生成了一个证明模式,并在 97 轮对话回合中进行了严格的推理,得出「P≠ NP」的结论,这与(Xu 和 Zhou,2023)结论一致 。

请点击以下链接查看论文:https://arxiv.org/pdf/2309.05689.pdf
本文的主要贡献可以总结为:
重写后的内容:该段落中提到,他们将框架命名为「苏格拉底推理」是受到了古希腊哲学家苏格拉底的启发。苏格拉底曾经说过:「我无法教给任何人任何东西。我只能让他们思考。」而该框架的整体设计思路也是如此,它是一种通用的问题解决框架,允许LLM在广泛的解决方案空间中导航并有效地得出答案
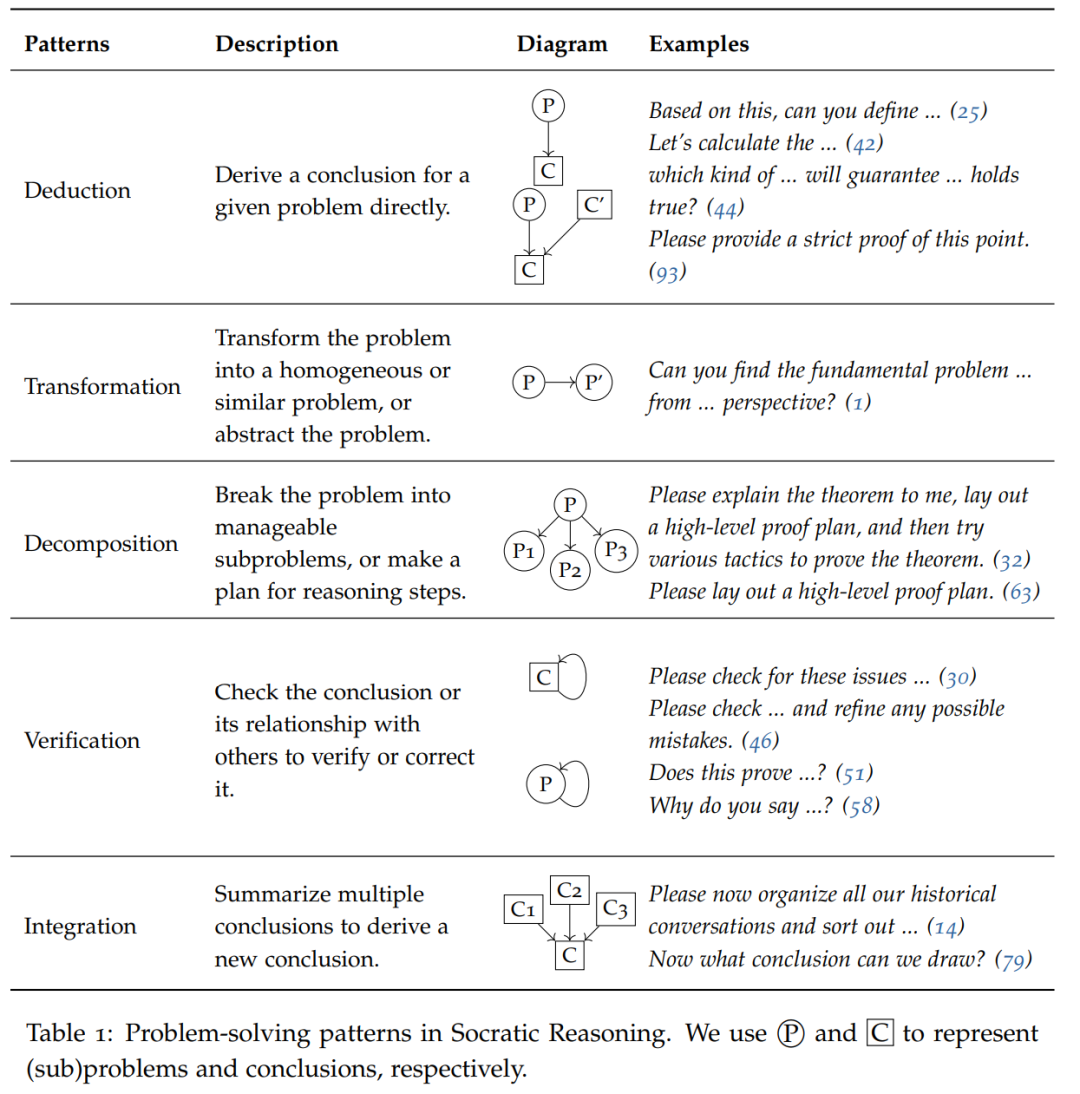
表1中列举了「苏格拉底推理」的五种提示模式:演绎、变换、分解、验证和融合。这些模式被用于发现新的见解和观点,将复杂的问题分解成子问题或小步骤,并通过挑战响应答案来进行自我改进
在较小的问题(atomic problem)上,LLM 能够直接给出推理结果,这时采用演绎模式(例如提示语为让我们一步一步思考……)来指导 LLM 直接得出结论。
对于更加复杂的问题,本文首先要求 LLM 将问题转化成一个新问题或将其分解为几个子问题。然后递归地执行这些模式,直到达到原子 ji 问题。
在出现新问题或得出新结论时,应采用验证模式并利用LLM的自我评估能力进行验证和改进
最后,融合模式要求LLM根据子问题的结果综合结论
通过一系列对话递归地激励 LLM 继续上述过程,直到解决目标问题
在这个工作中,「苏格拉底推理」为具有挑战性的问题提供了一个系统的提示框架
下图为「苏格拉底推理」中用于解决 P vs. NP 问题的对话示例。案例研究中使用了 GPT-4 API,此外,本文还根据轮次索引对流程进行排序。

在探索过程中,本文引入了五个不同的角色作为辅助证明者,例如精通概率论的数学家。实验总共进行了97轮对话,分为前14轮和后83轮对话
举个例子,第一轮提示:你能够从哲学的角度而不是从计算机理论的角度,找到P!=NP背后的根本问题吗?

以下是其他的提示:


对话不断进行,最终一轮对话如下:最后得出结论 P≠ NP

感兴趣的读者可以查看原论文,了解更多内容。
Atas ialah kandungan terperinci GPT-4通过97轮对话探索全球难题,得出P≠NP的结论. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Kekunci yang manakah harus saya tekan untuk memulihkan apabila saya tidak boleh menaip pada papan kekunci komputer saya?
Kekunci yang manakah harus saya tekan untuk memulihkan apabila saya tidak boleh menaip pada papan kekunci komputer saya? Apakah perbezaan antara golang dan ular sawa
Apakah perbezaan antara golang dan ular sawa Bagaimana untuk mendaftar nama domain laman web kekal
Bagaimana untuk mendaftar nama domain laman web kekal Apa itu ECharts
Apa itu ECharts Apakah peralatan yang diperlukan untuk siaran langsung Douyin?
Apakah peralatan yang diperlukan untuk siaran langsung Douyin? Bagaimana untuk menyelesaikan ralat pangkalan data discuz
Bagaimana untuk menyelesaikan ralat pangkalan data discuz Apakah alat perangkak percuma?
Apakah alat perangkak percuma? Bagaimana untuk mematikan komputer anda dengan cepat
Bagaimana untuk mematikan komputer anda dengan cepat



