
Mari kita lihat cara mengira bilangan segi tiga pada satah diberi n mata, dan hadkan bilangan titik kolinear kepada tidak lebih daripada dua.
Mengira bilangan segi tiga dalam satah dengan tidak lebih daripada dua titik kolinear ialah masalah biasa dalam geometri pengiraan, yang digunakan dalam grafik komputer, pemprosesan imej dan bidang sains komputer yang lain.
Sebagai contoh, apabila mencipta imej 2D daripada pemandangan 3D dalam grafik 3D, masalah mungkin timbul untuk mengira segi tiga dalam satah yang tidak lebih daripada dua titik kolinear. Dalam kes ini, proses pengiraan segi tiga boleh digunakan untuk menentukan bilangan segi tiga yang terdapat dalam imej 2D akhir selepas menayangkan pemandangan 3D pada satah. Ini membolehkan anda menentukan kerumitan adegan dan meningkatkan kelajuan pemaparan.
Dalam pemprosesan imej, kita mungkin ingin mengira bilangan objek atau bentuk unik dalam imej, soalan ini berguna. Dalam kes ini, kita boleh mewakili imej sebagai koleksi mata pada satah, dan kemudian kita boleh mengira bilangan segi tiga yang boleh dibuat antara titik ini dengan menggunakan teknik mengira segi tiga. Kita boleh menentukan anggaran bilangan item atau bentuk yang berbeza dalam imej dengan mengira bilangan segi tiga yang terbentuk.
Mari kita memahami masalah ini melalui beberapa contoh dan cuba menyelesaikannya.
Tujuannya adalah untuk menentukan berapa banyak segitiga yang terbentuk pada satah dengan n titik supaya tidak lebih daripada dua titik adalah kolinear.
Contoh -
Anggap N ialah bilangan mata pada pesawat.
N = 3
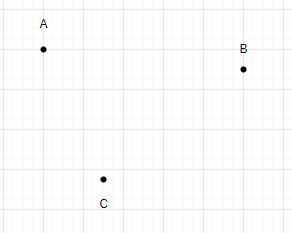
Menggunakan mata ini kita hanya boleh melukis segitiga.
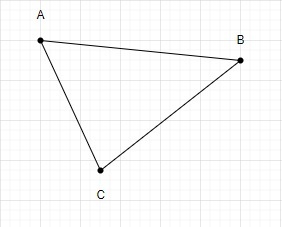
Jadi jumlah bilangan segi tiga yang terbentuk menggunakan 3 titik ialah 1.
Misalkan N = 4
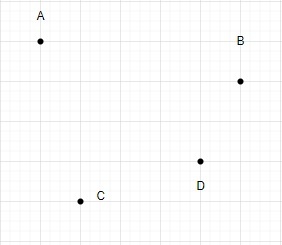
Mari lukis segitiga menggunakan empat titik ini.
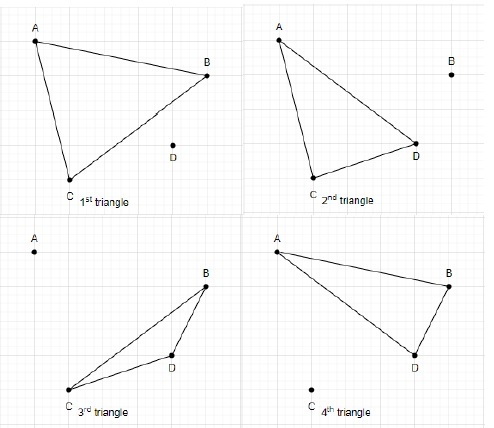
Jumlah bilangan segi tiga yang terbentuk menggunakan 4 titik ialah 4.
Mari kita lihat beberapa matematik yang terlibat dalam pengiraan bilangan segi tiga. Ini boleh diperoleh menggunakan pilih atur dan kombinasi. Untuk membina segitiga, anda memerlukan 3 mata daripada jumlah pada satu masa.
Oleh itu, jika satah mengandungi n titik dan tidak lebih daripada dua daripadanya adalah kolinear, maka bilangan segi tiga dalam satah itu diberikan oleh formula berikut.
$$mathrm{n_{C_{3}}:=:frac{n(n-1):(n-2)}{6}}$$
Atur cara mencari bilangan segi tiga dalam satah jika tidak lebih daripada dua titik adalah kolinear, menggunakan algoritma berikut.
Ambil bilangan mata pada satah sebagai input dan hadkannya kepada tidak lebih daripada dua titik kolinear.
Kira jumlah bilangan segi tiga menggunakan formula di atas.
Cetak jumlah bilangan segi tiga sebagai output.
Aturcara C++ untuk mengira bilangan segi tiga dalam satah jika tidak lebih daripada dua titik adalah kolinear.
#includeusing namespace std; int main() { int number_of_points = 4; int number_of_triangle; number_of_triangle = number_of_points * (number_of_points - 1) * (number_of_points - 2) / 6; cout << "Total number of triangles formed using " << number_of_points<< " points = " << number_of_triangle << endl; return 0; }
Total number of triangles formed using 4 points = 4
Kerumitan Masa: O(1) kerana kod ini melakukan bilangan pengiraan tetap tanpa mengira saiz input.
Kerumitan Ruang: O(1) kerana kod menggunakan bilangan pembolehubah tetap untuk menyimpan nilai input dan hasil tanpa mengira saiz input.
Dalam artikel ini, kami cuba menerangkan kaedah untuk mencari jumlah bilangan segitiga yang mungkin dengan n titik yang diberikan, dengan kekangan bahawa tiada dua titik adalah kolinear. Saya harap artikel ini membantu anda mempelajari konsep ini dengan lebih baik.
Atas ialah kandungan terperinci Jika tidak lebih daripada dua titik dalam satah adalah kolinear, berapakah bilangan segi tiga?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




