Keupayaan aritmetik hampir kepada skor sempurna! Universiti Nasional Singapura mengeluarkan Kambing, yang membunuh GPT-4 dengan hanya 7 bilion parameter dan pada mulanya menyokong pendaraban dan pembahagian 16 digit.

Walaupun model bahasa berskala besar telah menunjukkan prestasi unggul dalam pelbagai tugas pemprosesan bahasa semula jadi, masalah aritmetik masih menjadi kesukaran besar, walaupun untuk GPT- 4 yang paling berkuasa juga sukar untuk ditangani dengan masalah asas aritmetik.

Baru-baru ini, penyelidik dari Universiti Nasional Singapura mencadangkan Kambing, model yang didedikasikan untuk aritmetik Selepas penalaan halus pada model LLaMA, ia mencapai prestasi yang jauh lebih baik daripada GPT-4 kemahiran.

Pautan kertas: https://arxiv.org/pdf/2305.14201.pdf

Dengan menala halus pada set data aritmetik sintetik, Goat mencapai prestasi terkini pada subtugas aritmetik BIG-bench,

Kambing Melalui penalaan halus diselia sahaja, adalah mungkin untuk mencapai ketepatan yang hampir sempurna dalam operasi penambahan dan penolakan bilangan besar, mengatasi semua model bahasa pra-latihan sebelumnya, seperti Bloom, OPT, GPT-NeoX, dll. Antaranya, sampel sifar Kambing-7B mencapai Ketepatan malah melebihi PaLM-540 selepas pembelajaran beberapa pukulan Para penyelidik mengaitkan prestasi cemerlang Kambing dengan teknologi pembahagian kata LLaMA yang konsisten untuk nombor.

Untuk menyelesaikan tugasan yang lebih mencabar seperti pendaraban dan pembahagian nombor besar, penyelidik juga mencadangkan kaedah untuk mengklasifikasikan tugasan mengikut kebolehpelajaran aritmetik dan kemudian menggunakan prinsip asas aritmetik memecahkan bukan- tugasan yang boleh dipelajari, seperti pendaraban dan pembahagian berbilang digit, ke dalam urutan tugasan yang boleh dipelajari.

Selepas pengesahan percubaan menyeluruh, langkah penguraian yang dicadangkan dalam artikel boleh meningkatkan prestasi aritmetik dengan berkesan.

Dan Goat-7 B boleh dilatih dengan cekap menggunakan LoRA pada GPU VRAM 24 GB, penyelidik lain boleh mengulangi eksperimen dengan mudah, model, set data dan ular sawa yang menghasilkan dataset Skrip akan menjadi sumber terbuka tidak lama lagi.

Model bahasa yang boleh dikira

LLaMA Ia ialah satu set model bahasa pra-latihan sumber terbuka yang dilatih pada trilion token menggunakan set data yang tersedia secara umum dan mencapai prestasi terkini pada berbilang penanda aras.

Hasil penyelidikan terdahulu menunjukkan bahawa tokenisasi adalah penting untuk keupayaan aritmetik LLM, tetapi teknik tokenisasi yang biasa digunakan tidak boleh mewakili nombor dengan baik, contohnya, nombor dengan terlalu banyak digit mungkin akan dibahagikan.

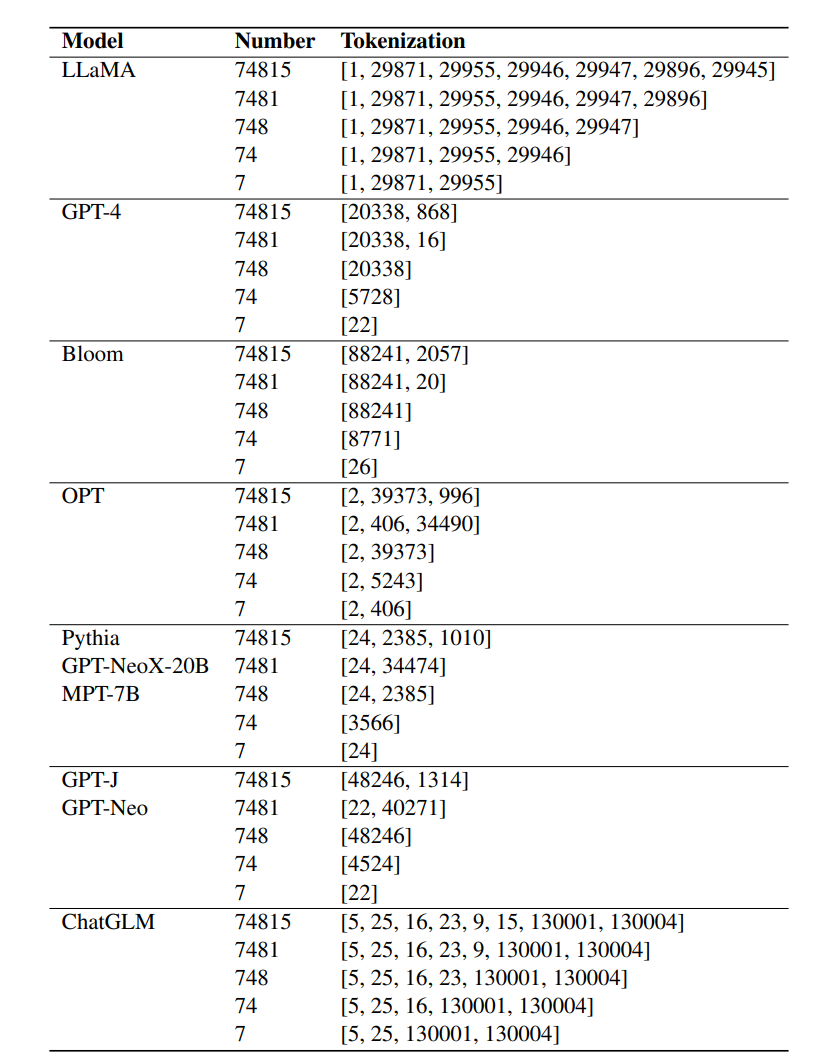LLaMA memilih untuk membahagikan nombor kepada berbilang token untuk memastikan ketekalan perwakilan digital Keupayaan aritmetik luar biasa yang ditunjukkan dalam keputusan adalah disebabkan terutamanya oleh pembahagian nombor LLaMA yang konsisten.

Dalam percubaan, model bahasa diperhalusi lain, seperti Bloom, OPT, GPT-NeoX dan Pythia, tidak dapat memadankan keupayaan aritmetik LLaMA.

Sebelum ini Pengkaji menjalankan analisis teori menggunakan perantaraan penyeliaan untuk menyelesaikan tugasan komposit dan menunjukkan bahawa tugasan tersebut tidak boleh dipelajari tetapi boleh diuraikan kepada nombor polinomial subtugasan mudah.

Iaitu, masalah kompaun yang tidak boleh dipelajari boleh dipelajari dengan menggunakan penyeliaan pertengahan atau rantaian langkah (CoT).

Berdasarkan analisis ini, penyelidik mula-mula mengelaskan tugasan yang boleh dipelajari dan tidak boleh dipelajari secara eksperimen.

Dalam konteks pengkomputeran aritmetik, tugasan yang boleh dipelajari secara amnya merujuk kepada tugasan yang mana model boleh dilatih dengan jayanya untuk menjana jawapan secara langsung, dengan itu mencapai tahap yang cukup tinggi dalam bilangan yang telah ditetapkan. zaman latihan.

Tugas yang tidak boleh dipelajari ialah tugasan yang model mengalami kesukaran belajar dengan betul dan menjana jawapan langsung walaupun selepas latihan yang meluas.

Walaupun sebab yang tepat di sebalik perubahan dalam kebolehpelajaran tugasan tidak difahami sepenuhnya, ia boleh dihipotesiskan bahawa ia berkaitan dengan kerumitan corak asas dan saiz memori kerja yang diperlukan untuk melengkapkan tugas itu.

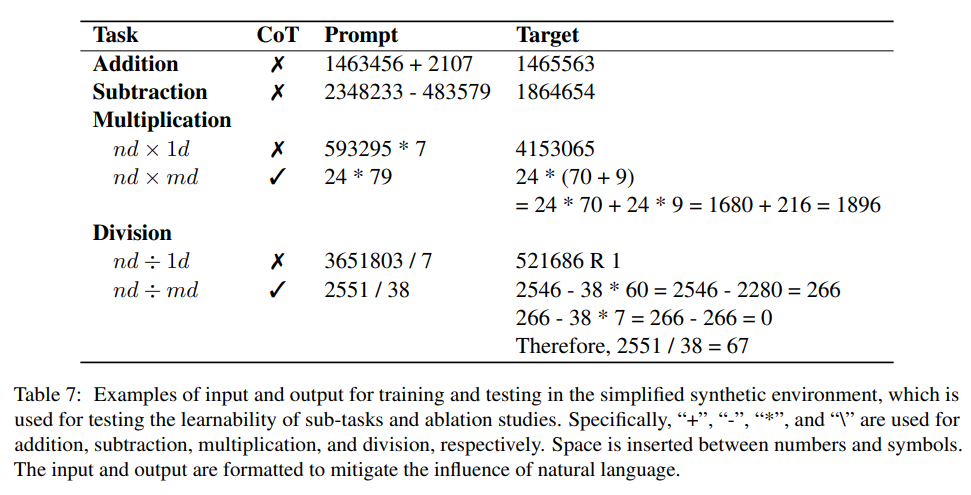
Para penyelidik secara eksperimen mengkaji kebolehlaksanaan tugas-tugas ini dengan memperhalusi model khusus untuk setiap tugasan dalam sintetik yang dipermudahkan. persekitaran.

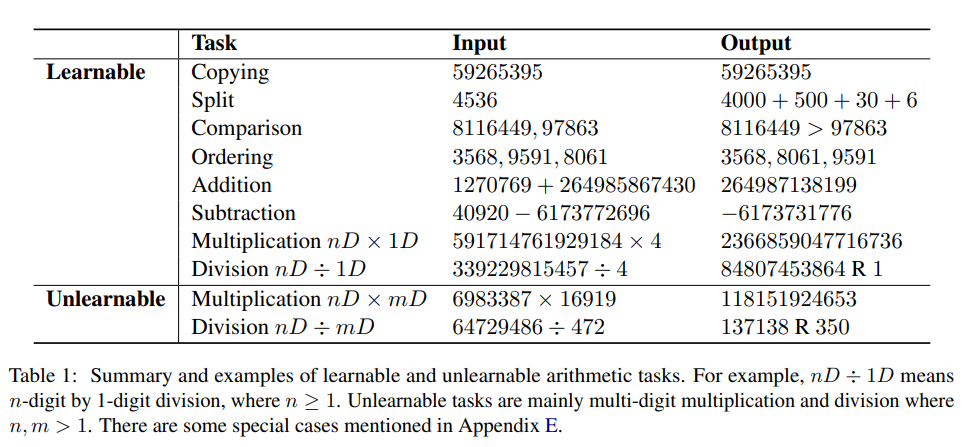
Tugas yang boleh dipelajari dan tidak boleh dipelajari

Hasil pengkelasan tugasan juga sama seperti persepsi manusia Dengan amalan, manusia boleh mengira penambahan dan penolakan dua nombor besar dalam fikiran mereka, terus dari kiri (digit paling bererti) ke kanan tanpa pengiraan secara manual ) Tulis jawapan berangka akhir.

Tetapi aritmetik mental untuk menyelesaikan pendaraban dan pembahagian nombor besar adalah tugas yang mencabar.

Dapat juga diperhatikan bahawa hasil pengelasan tugas di atas juga konsisten dengan prestasi GPT-4 Khususnya, GPT-4 pandai menjana jawapan langsung untuk penambahan dan penolakan nombor besar, apabila ia datang kepada Ketepatan menurun dengan ketara apabila ia melibatkan tugas pendaraban dan pembahagian berbilang bit.

Ketidakupayaan model berkuasa seperti GPT-4 untuk menyelesaikan secara langsung tugasan yang tidak boleh dipelajari juga mungkin menunjukkan bahawa menjana jawapan langsung untuk tugasan ini amat mencabar walaupun selepas latihan yang meluas .

Perlu diambil perhatian bahawa tugasan yang boleh dipelajari untuk LLaMA mungkin tidak semestinya boleh dipelajari untuk LLM lain.

Selain itu, bukan semua tugasan yang diklasifikasikan sebagai tidak boleh dipelajari sama sekali mustahil untuk model belajar.

Sebagai contoh, mendarab nombor dua digit dengan nombor dua digit dianggap sebagai tugas yang tidak boleh dipelajari, tetapi jika set latihan mengandungi semua data penghitungan pendaraban 2 digit yang mungkin, model masih melakukan Jawapan boleh dijana secara langsung dengan memasang set latihan terlebih dahulu.

Walau bagaimanapun, keseluruhan proses memerlukan hampir 10 zaman untuk mencapai ketepatan kira-kira 90%.

Dengan memasukkan CoT yang dicadangkan dalam artikel sebelum jawapan akhir, model boleh mencapai ketepatan yang agak baik dalam pendaraban dua digit selepas 1 zaman latihan, yang juga konsisten dengan Kajian terdahulu telah secara konsisten membuat kesimpulan bahawa kehadiran penyeliaan pertengahan memudahkan proses pembelajaran.

Tambahan dan penolakan

Kedua-dua operasi aritmetik ini boleh dipelajari, hanya melalui penalaan halus diselia, model Ia menunjukkan keupayaan luar biasa untuk menjana jawapan berangka langsung dengan tepat.

Ini terbukti daripada fakta bahawa model itu mencapai ketepatan hampir sempurna pada set ujian yang tidak kelihatan, walaupun dilatih pada subset data tambahan yang sangat terhad, model itu berjaya menangkap corak asas operasi aritmetik tanpa menggunakan CoT

Eksperimen telah mengesahkan bahawa pendaraban nombor n-digit dengan nombor satu digit boleh dipelajari, tetapi pendaraban berbilang digit tidak boleh dipelajari .

Untuk mengatasi masalah ini, penyelidik memilih untuk memperhalusi LLM untuk menjana CoT sebelum menjana jawapan, memecahkan pendaraban berbilang digit kepada 5 subtugas yang boleh dipelajari:

1. Pengekstrakan, mengekstrak ungkapan aritmetik daripada arahan bahasa semula jadi

2. Bahagikan, membahagikan yang lebih baik daripada dua nombor kecil dipecahkan kepada nilai tempat

3. Pengembangan, penjumlahan berdasarkan pengembangan pengedaran

4, kira setiap produk secara serentak

5 penggal demi penggal, tambah dua sebutan pertama, salin istilah yang tinggal dan dapatkan jumlah akhir

Setiap satu daripada ini tugas boleh dipelajari.

Pembahagian

Begitu juga, boleh diperhatikan secara eksperimen bahawa membahagi n digit dengan 1 digit boleh dipelajari, manakala pembahagian berbilang digit tidak boleh dipelajari.

Para penyelidik mereka bentuk gesaan rantaian pemikiran baharu menggunakan persamaan rekursi yang memperbaik pembahagian perlahan.

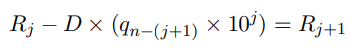
Idea utama ialah menolak gandaan dividen daripada dividen sehingga bakinya kurang daripada pembahagi.

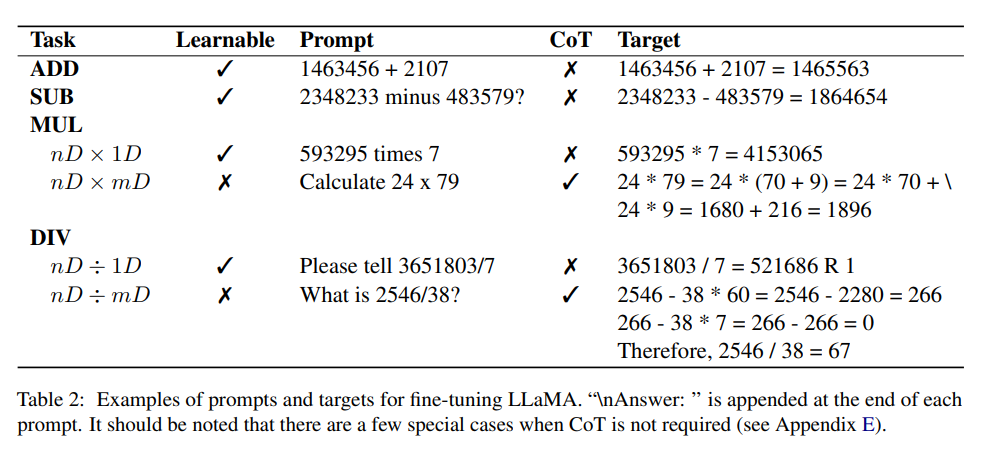
Dataset

Direka dalam artikel Percubaan ialah penambahan dan penolakan dua integer positif, setiap integer positif mengandungi sehingga 16 digit, dan hasil operasi tolak mungkin nombor negatif.

Untuk mengehadkan panjang jujukan maksimum yang dihasilkan, hasil pendaraban ialah integer positif dalam 12 digit dalam pembahagian dua integer positif, dividen adalah kurang daripada 12 digit dan hasil bagi adalah dalam 6 digit.

Penyelidik menggunakan skrip Python untuk mensintesis set data yang menghasilkan kira-kira 1 juta pasangan soalan-jawapan. Jawapan mengandungi CoT yang dicadangkan dan output berangka akhir. , yang menjamin bahawa kebarangkalian contoh pendua adalah sangat rendah, tetapi bilangan yang kecil boleh diambil beberapa kali.

Penalaan halus

Untuk membolehkan model menyelesaikan masalah aritmetik berdasarkan arahan dan memudahkan menjawab soalan bahasa semula jadi , penyelidik Beratus-ratus templat arahan dijana menggunakan ChatGPT.

Semasa proses penalaan arahan, templat dipilih secara rawak daripada set latihan untuk setiap input aritmetik dan LLaMA-7B yang diperhalusi, serupa dengan kaedah yang digunakan dalam Alpaca.

Goat-7B boleh diperhalusi menggunakan LoRA pada GPU VRAM 24GB, hanya mengambil masa kira-kira 1.5 jam untuk melengkapkan 100,000 sampel pada GPU A100 penalaan halus dan mencapai ketepatan yang hampir sempurna.

Keputusan eksperimen

Nampaknya tidak adil untuk membandingkan prestasi Kambing dan GPT-4 pada pendaraban dan pembahagian yang besar, kerana GPT-4 menjana jawapan secara langsung, manakala Goat It bergantung pada rantai pemikiran reka bentuk, jadi semasa penilaian GPT-4, "Selesaikannya langkah demi langkah" telah ditambahkan pada penghujung setiap gesaan

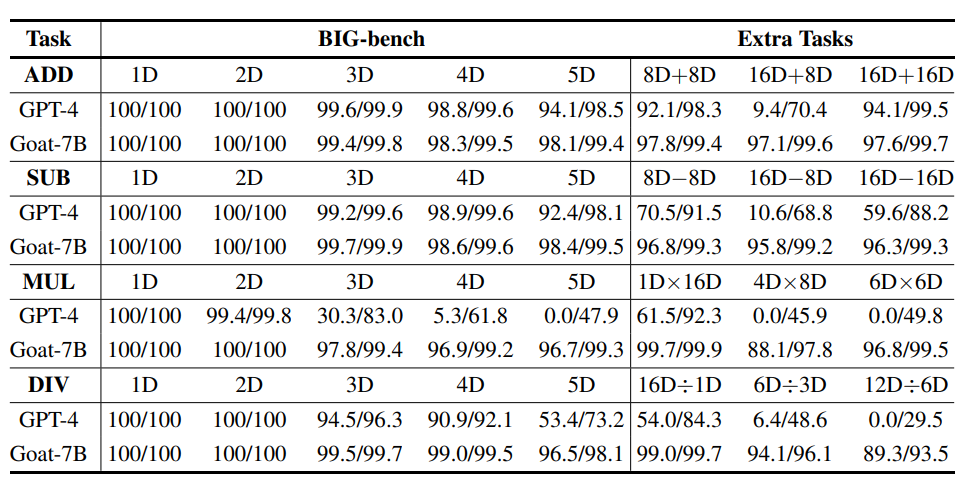
Walau bagaimanapun, dapat diperhatikan bahawa walaupun GPT-4 dalam beberapa kes, langkah perantaraan pendaraban dan pembahagian panjang adalah salah, jawapan akhir masih betul, yang bermaksud GPT-4 tidak menggunakan pemikiran Penyeliaan pertengahan rantaian untuk menambah baik keluaran akhir.

3 ralat biasa berikut akhirnya dikenal pasti daripada penyelesaian GPT-4:

1 Penjajaran nombor yang sepadan

2. Nombor berulang

3 Hasil perantaraan darab n digit dengan 1 digit adalah salah

Daripada eksperimen Ia boleh dilihat daripada keputusan bahawa GPT-4 berprestasi agak baik pada tugasan 8D+8D dan 16D+16D, tetapi keputusan pengiraan pada kebanyakan tugasan 16D+8D adalah salah, walaupun secara intuitif, 16D+8D sepatutnya lebih mudah daripada 16D+ 16D.

Walaupun punca sebenar perkara ini tidak jelas, satu faktor yang mungkin adalah proses pembahagian digit GPT-4 yang tidak konsisten, menjadikannya sukar untuk menjajarkan antara dua digit

Atas ialah kandungan terperinci Keupayaan aritmetik hampir kepada skor sempurna! Universiti Nasional Singapura mengeluarkan Kambing, yang membunuh GPT-4 dengan hanya 7 bilion parameter dan pada mulanya menyokong pendaraban dan pembahagian 16 digit.. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!