当插入第i(i>=1)个元素时，前面的array[0],array[1],…,array[i-1]已经排好序，此时用array[i]与array[i-1],array[i-2],…进行比较，找到插入位置即将array[i]插入，原来位置上的元素顺序后移。
数据越接近有序，直接插入排序的时间消耗越少。
时间复杂度：O(N^2)
空间复杂度O(1)，是一种稳定的算法
直接插入排序：
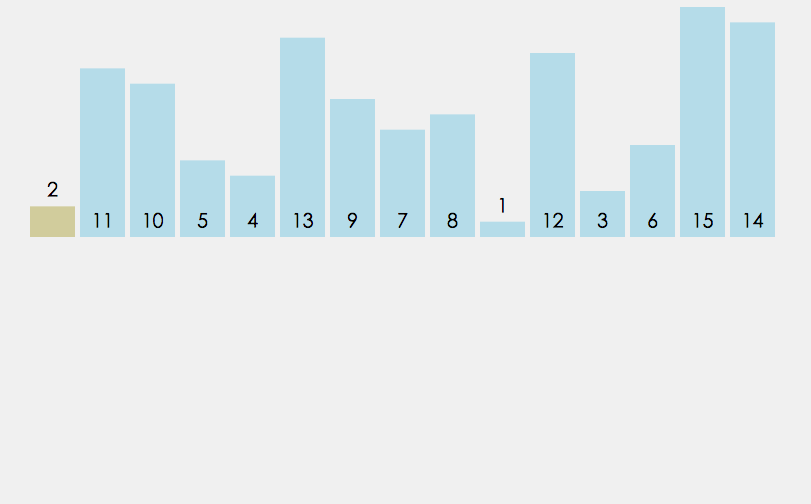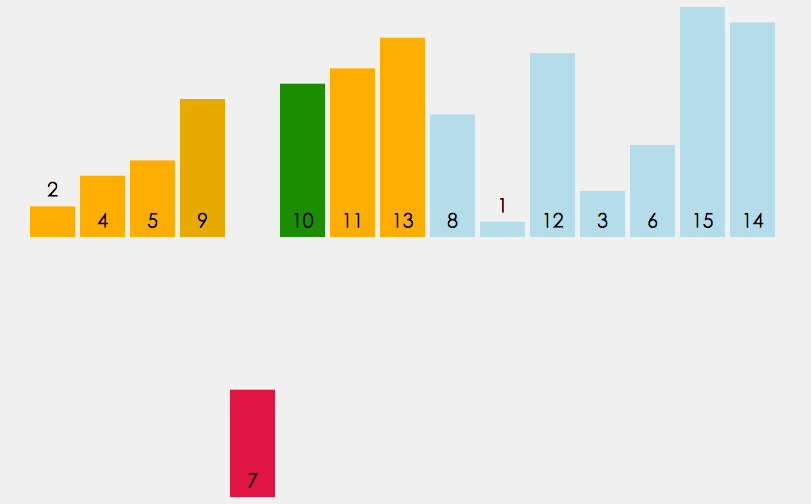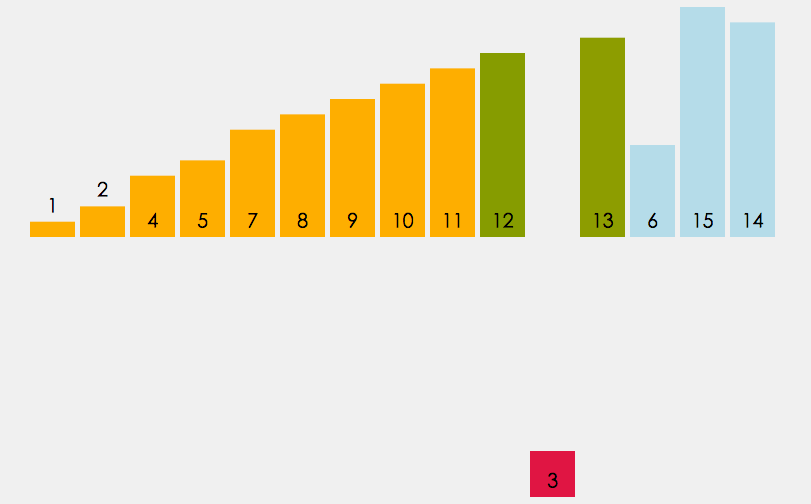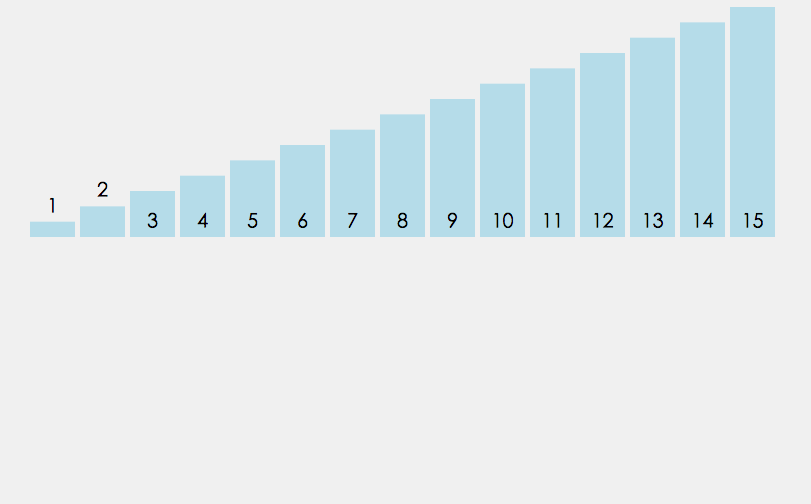
public static void insertSort(int[] array){ for (int i = 1; i < array.length; i++) { int tmp=array[i]; int j=i-1; for(;j>=0;--j){ if(array[j]>tmp){ array[j+1]=array[j]; }else{ break; } } array[j+1]=tmp; } }
希尔排序法的基本思想是：先选定一个整数gap，把待排序文件中所有记录分成gap个组，所有距离为gap的数分在同一组内，并对每一组内的数进行直接插入排序。然后取gap=gap/2，重复上述分组和排序的工作。当gap=1时，所有数在一组内进行直接插入排序。
希尔排序是对直接插入排序的优化。
目的是让数组更接近于有序，因此当gap > 1时进行预排序。插入排序在gap为1时可以快速地对接近有序的数组进行排序。
希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算。
希尔排序 ：
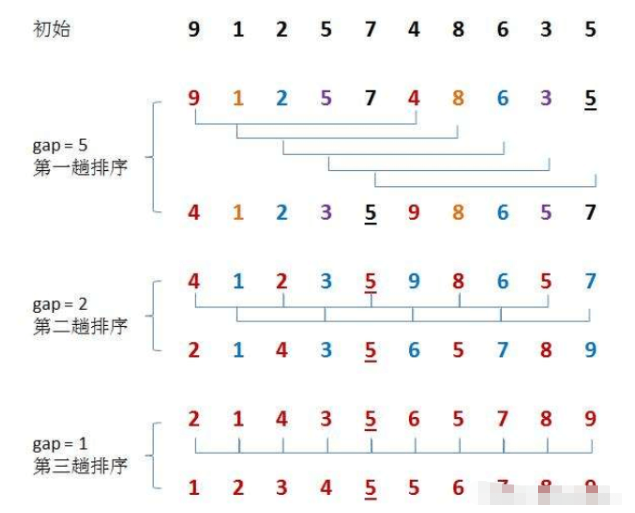
public static void shellSort(int[] array){ int size=array.length; //这里定义gap的初始值为数组长度的一半 int gap=size/2; while(gap>0){ //间隔为gap的直接插入排序 for (int i = gap; i < size; i++) { int tmp=array[i]; int j=i-gap; for(;j>=0;j-=gap){ if(array[j]>tmp){ array[j+gap]=array[j]; }else{ break; } } array[j+gap]=tmp; } gap/=2; } }
在元素集合array[i]--array[n-1]中选择最小的数据元素
若它不是这组元素中的第一个，则将它与这组元素中的第一个元素交换
在剩余的集合中，重复上述步骤，直到集合剩余1个元素
时间复杂度：O(N^2)
空间复杂度为O(1)，不稳定
选择排序 ：
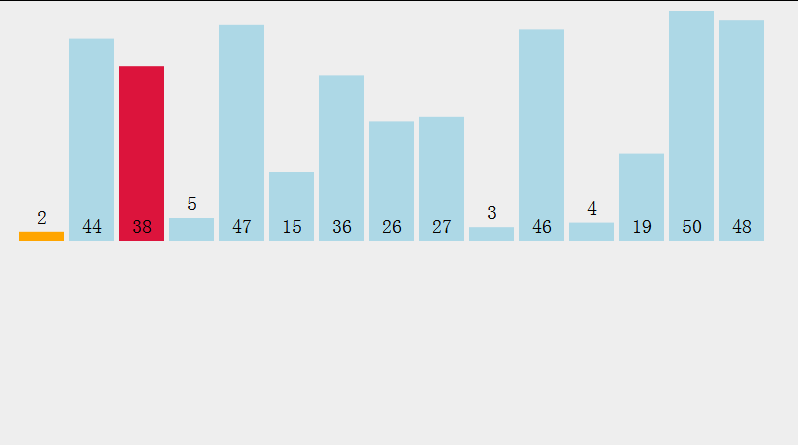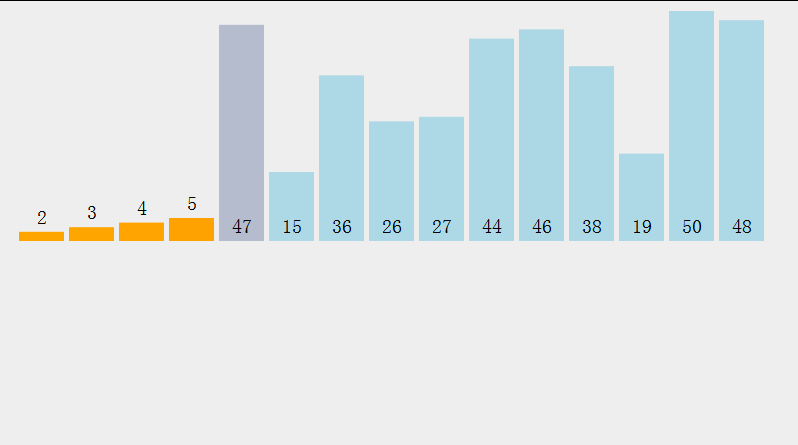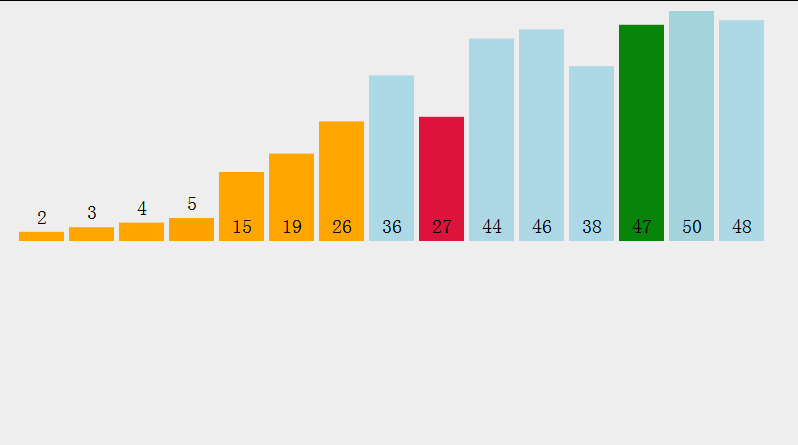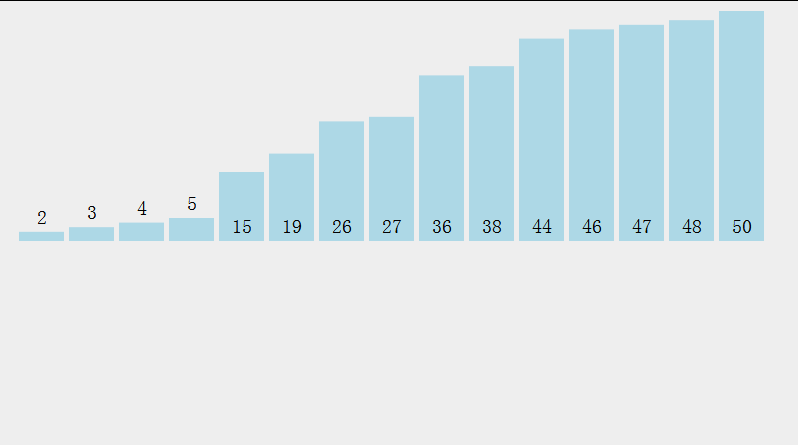
//交换 private static void swap(int[] array,int i,int j){ int tmp=array[i]; array[i]=array[j]; array[j]=tmp; } //选择排序 public static void chooseSort(int[] array){ for (int i = 0; i < array.length; i++) { int minIndex=i;//记录最小值的下标 for (int j = i+1; j < array.length; j++) { if (array[j]
Salin selepas log masuk
堆排序的两种思路（以升序为例）：
创建小根堆，依次取出堆顶元素放入数组中，直到堆为空
创建大根堆，定义堆的尾元素位置key，每次交换堆顶元素和key位置的元素（key--），直到key到堆顶，此时将堆中元素层序遍历即为升序（如下）
时间复杂度：O(N^2)
空间复杂度：O(N)，不稳定
堆排序：
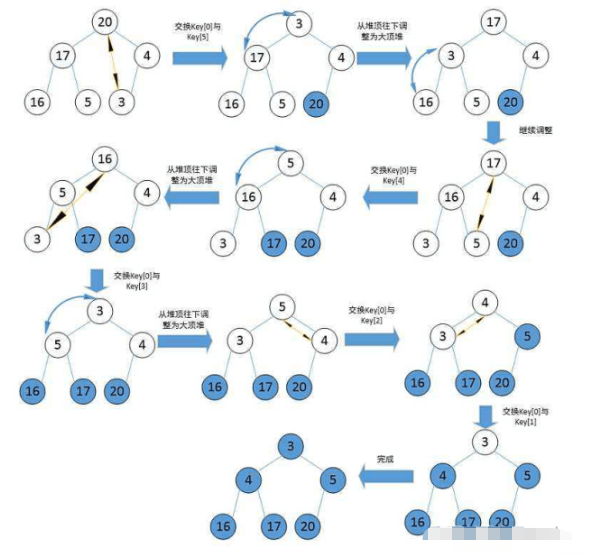
//向下调整 public static void shiftDown(int[] array,int parent,int len){ int child=parent*2+1; while(childarray[child]){ child++; } } if(array[child]>array[parent]){ swap(array,child,parent); parent=child; child=parent*2+1; }else{ break; } } } //创建大根堆 private static void createHeap(int[] array){ for (int parent = (array.length-1-1)/2; parent >=0; parent--) { shiftDown(array,parent,array.length); } } //堆排序 public static void heapSort(int[] array){ //创建大根堆 createHeap(array); //排序 for (int i = array.length-1; i >0; i--) { swap(array,0,i); shiftDown(array,0,i); } }
两层循环，第一层循环表示要排序的趟数，第二层循环表示每趟要比较的次数；这里的冒泡排序做了优化，在每一趟比较时，我们可以定义一个计数器来记录数据交换的次数，如果没有交换，则表示数据已经有序，不需要再进行排序了。
时间复杂度：O(N^2)
空间复杂度为O(1),是一个稳定的排序
冒泡排序：
public static void bubbleSort(int[] array){ for(int i=0;iarray[j+1]){ swap(array,j,j+1); count++; } } if(count==0){ break; } } }
任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。
时间复杂度：最好O(n*logn):每次可以尽量将待排序的序列均匀分割
最坏O(N^2)：待排序序列本身是有序的
空间复杂度：最好O(logn)、 最坏O(N)。不稳定的排序
（1）挖坑法
当数据有序时，快速排序就相当于二叉树没有左子树或右子树，此时空间复杂度会达到O(N)，如果大量数据进行排序，可能会导致栈溢出。
public static void quickSort(int[] array,int left,int right){ if(left>=right){ return; } int l=left; int r=right; int tmp=array[l]; while(l=tmp&&l
Salin selepas log masuk
（2）快速排序的优化
三数取中法选key
关于key值的选取，如果待排序序列是有序的，那么我们选取第一个或最后一个作为key可能导致分割的左边或右边为空，这时快速排序的空间复杂度会比较大，容易造成栈溢出。那么我们可以采用三数取中法来取消这种情况。以序列中第一个、最后一个和中间一个元素的中间值作为key值。
//key值的优化，只在快速排序中使用，则可以为private private int threeMid(int[] array,int left,int right){ int mid=(left+right)/2; if(array[left]>array[right]){ if(array[mid]>array[left]){ return left; } return array[mid]array[right]?right:mid; } }
递归到小的子区间时，可以考虑用插入排序
随着我们递归的进行，区间会变的越来越小，我们可以在区间小到一个值的时候，对其进行插入排序，这样代码的效率会提高很多。
（3）快速排序的非递归实现
//找到一次划分的下标 public static int patition(int[] array,int left,int right){ int tmp=array[left]; while(left=tmp){ right--; } array[left]=array[right]; while(left stack=new Stack<>(); int left=0; int right=array.length-1; stack.push(left); stack.push(right); while(!stack.isEmpty()){ int r=stack.pop(); int l=stack.pop(); int p=patition(array,l,r); if(p-1>l){ stack.push(l); stack.push(p-1); } if(p+1
Salin selepas log masuk
归并排序（MERGE-SORT）：该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。实现序列的完全有序，需要将已经有序的子序列合并，即先让每个子序列有序，然后再将相邻的子序列段有序。若将两个有序表合并成一个有序表，称为二路归并。
时间复杂度：O(n*logN)（无论有序还是无序）
空间复杂度：O（N）。是稳定的排序。
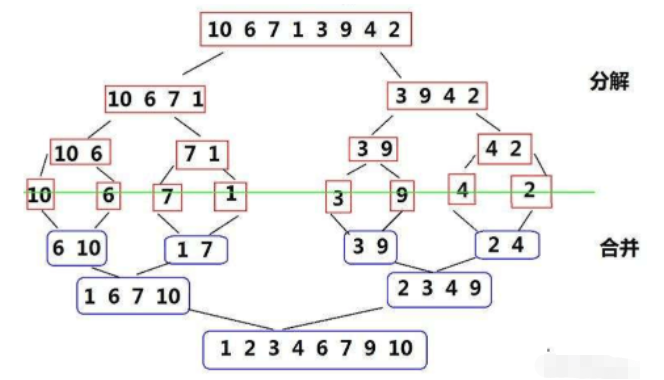
//归并排序：递归 public static void mergeSort(int[] array,int left,int right){ if(left>=right){ return; } int mid=(left+right)/2; //递归分割 mergeSort(array,left,mid); mergeSort(array,mid+1,right); //合并 merge(array,left,right，mid); } //非递归 public static void mergeSort1(int[] array){ int gap=1; while(gap=array.length){ mid=array.length-1; } int right=left+2*gap-1; if(right>=array.length){ right=array.length-1; } merge(array,left,right,mid); } gap=gap*2; } } //合并：合并两个有序数组 public static void merge(int[] array,int left,int right，int mid){ int[] tmp=new int[right-left+1]; int k=0; int s1=left; int e1=mid; int s2=mid+1; int e2=right; while(s1<=e1&&s2<=e2){ if(array[s1]<=array[s2]){ tmp[k++]=array[s1++]; }else{ tmp[k++]=array[s2++]; } } while(s1<=e1){ tmp[k++]=array[s1++]; } while(s2<=e2){ tmp[k++]=array[s2++]; } for (int i = left; i <= right; i++) { array[i]=tmp[i-left]; } }
| 排序方法 | 最好时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
| 直接插入排序 | O(n) | O(n^2) | O(1) | 稳定 |
| 希尔排序 | O(n) | O(n^2) | O(1） | 不稳定 |
| 直接排序 | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(nlog(2)n) | O(nlog(2)n) | O(1) | 不稳定 |
| 冒泡排序 | O(n) | O(n^2) | O(1) | 稳定 |
| 快速排序 | O(nlog(2)n) | O(n^2) | O(nlog(2)n) | 不稳定 |
| 归并排序 | O(nlog(2)n) | O(nlog(2)n) | O(n) | 稳定 |
Atas ialah kandungan terperinci Java数据结构七大排序怎么使用. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
![[Web front-end] Permulaan pantas Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
