Bagaimana untuk melaksanakan pengisihan topologi di Jawa

Bayang-bayang

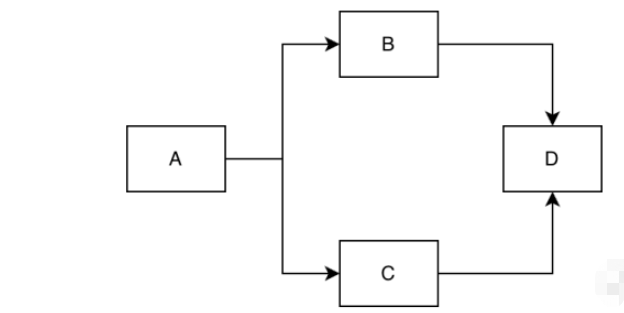
Kami akan memperkenalkan algoritma yang berkaitan dengan graf terarah dalam bahagian ini, jadi kami akan menerangkan beberapa konsep graf terarah terlebih dahulu tidak dijelaskan secara terperinci. Pertama, nod graf terarah disambungkan dengan garisan dengan anak panah. Darjah keluar dan dalam darjah nod boleh digunakan untuk menggambarkannya Apabila ekor sambungan menghala ke nod, darjah keluarnya akan meningkat sebanyak 1 dan apabila anak panah sambungan menghala ke nod, dalam darjahnya akan meningkat sebanyak 1. Lihat contoh berikut, A mempunyai darjah dalam 0 dan darjah luar 2, B mempunyai darjah dalam 1 dan darjah luar 1, C mempunyai darjah dalam 1 dan darjah keluar- darjah 1, D mempunyai darjah dalam 2 dan darjah keluar ialah 0.

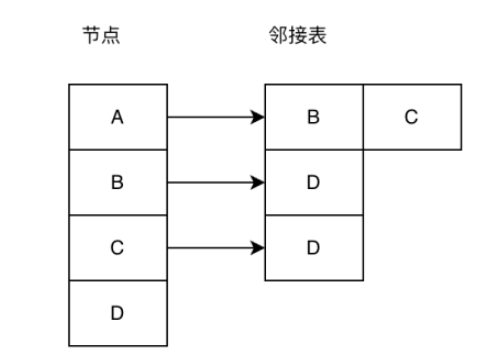
Senarai bersebelahan: Senarai bersebelahan ialah cara yang berkesan untuk menyimpan struktur graf Seperti yang ditunjukkan dalam rajah di bawah, tatasusunan nod di sebelah kiri menyimpan semua nod dalam graf, dan senarai bersebelahan di sebelah kanan menyimpan nod bersebelahan.

Pengenalan

Dalam artikel ini kita akan bercakap tentang pengisihan topologi, yang merupakan algoritma untuk graf acyclic terarah, terutamanya untuk menyelesaikan masalah prekursor. hubungan seterusnya, iaitu item apa yang perlu kita lengkapkan dahulu apabila melengkapkan item semasa, sebenarnya banyak digunakan dalam kawalan proses kita. Melihat gambar di bawah, kita perlu melengkapkan item A dahulu, dan kemudian kita boleh melengkapkan item B dan C. Perkara B dan C adalah selari dan tidak teratur, tetapi item D hanya boleh disiapkan selepas item B dan C selesai. Pengisihan topologi boleh membantu kita mencari susunan yang munasabah untuk melengkapkan item Pada masa yang sama, mari kita lihat contoh di atas Selepas item A selesai, item B dan C tidak mengikut urutan dipenuhi, jadi pengisihan topologi Urutan tertib tidak pasti sepenuhnya.

Proses kerja

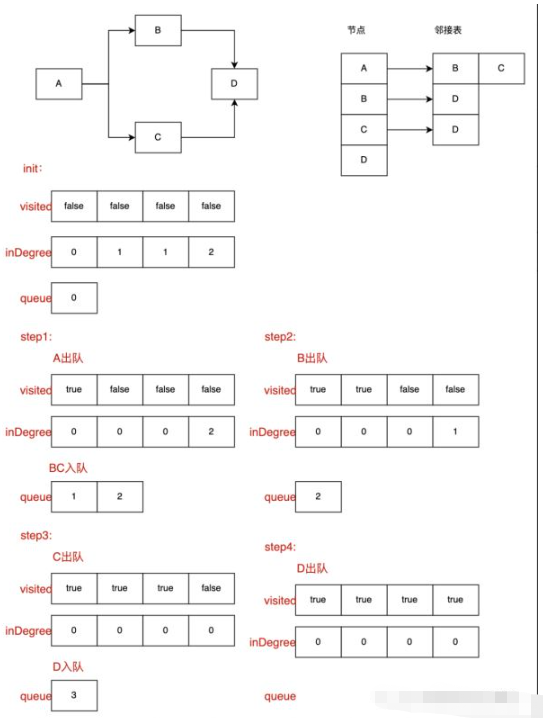
Pertama, pengisihan topologi sepadan dengan graf akiklik terarah. Untuk graf akiklik, mesti ada sekurang-kurangnya satu nod dengan tidak darjah 0. Dalam keadaan semasa, kita perlu mencari nod dengan darjah 0 untuk operasi dalam darjah 0 bermakna nod semasa tidak mempunyai nod pendahulu, atau nod pendahulu telah diproses dan boleh dikendalikan secara langsung. Selepas operasi selesai, semua dalam darjah nod pengganti nod semasa dikurangkan sebanyak 1, dan nod dengan nod dalam darjah 0 dicari semula untuk operasi. Selepas itu, ia adalah proses rekursif, dan nod dengan darjah 0 di bawah keadaan semasa diproses secara berterusan sehingga semua nod diproses.

Struktur data

Berikut ialah struktur graf terarah, di mana nod menyimpan semua nod dalam graf semasa dan adj menyimpan yang sepadan nod subskrip titik bersebelahan. Apabila memulakan graf, anda perlu menentukan bilangan nod, mencipta tatasusunan nod dan tatasusunan bersebelahan. Menyediakan kaedah bernama addEdge, yang digunakan untuk mewujudkan kelebihan antara dua nod, iaitu, untuk menambah nod pengganti pada senarai bersebelahan nod pendahulu.

public static class Graph{ /** * 节点个数 */ private Integer nodeSize; /** * 节点 */ private char[] node; /** * 邻接表 */ private LinkedList[] adj; public Graph(char[] node) { this.nodeSize = node.length; this.node = node; this.adj = new LinkedList[nodeSize]; for (int i = 0 ; i < adj.length ; i++) { adj[i] = new LinkedList(); } } /** * 在节点之间加边，前驱节点指向后继节点 * @param front 前驱节点所在下标 * @param end 后继节点所在下标 */ public void addEdge(int front, int end) { adj[front].add(end); } }

Isihan topologi

Isihan topologi mula-mula memulakan dua tatasusunan sementara, baris gilir dan tatasusunan inDegree untuk menyimpan dalam darjah nod langganan yang sepadan, kerana setiap nod yang dilawati memerlukan pendahulunya nod telah pun Selesai, iaitu, dalam darjah ialah 0. Dengan tatasusunan ini, kita boleh mencari nod ini secara relatifnya dengan cepat, yang menandakan sama ada nod semasa telah dilawati untuk menghalang beberapa lawatan; baris gilir disimpan dalam keadaan semasa Semua nod dengan indegree 0. (Perhatikan bahawa untuk kemudahan akses, kita semua menyimpan subskrip nod. Langkah1: Memulakan tatasusunan inDegree dan tatasusunan yang dilawati; langkah2: Melintasi tatasusunan inDegree dan meletakkan semua nod dengan indegree 0 ke dalam baris gilir nod; langkah3: Keluar dari nod nod dalam urutan; Tentukan sama ada nod semasa telah dilawati, jika ya, kembali ke langkah3, jika tidak, teruskan ke langkah seterusnya; , tentukan sama ada dalam darjah nod bersebelahan ialah 0, jika 0, letakkannya terus ke dalam baris gilir nod , jika bukan 0, kembali ke langkah3

/** * @param graph 有向无环图 * @return 拓扑排序结果 */ public List toPoLogicalSort(Graph graph) { //用一个数组标志所有节点入度 int[] inDegree = new int[graph.nodeSize]; for (LinkedList list : graph.adj) { for (Object index : list) { ++ inDegree[(int)index]; } } //用一个数组标志所有节点是否已经被访问 boolean[] visited = new boolean[graph.nodeSize]; //开始进行遍历 Deque nodes = new LinkedList<>(); //将入度为0节点入队 for (int i = 0 ; i < graph.nodeSize; i++) { if (inDegree[i] == 0) { nodes.offer(i); } } List result = new ArrayList<>(); //将入度为0节点一次出队处理 while (!nodes.isEmpty()) { int node = nodes.poll(); if (visited[node]) { continue; } visited[node] = true; result.add(graph.node[node]); //将当前node的邻接节点入度-1； for (Object list : graph.adj[node]) { -- inDegree[(int)list]; if (inDegree[(int)list] == 0) { //前驱节点全部访问完毕，入度为0 nodes.offer((int) list); } } } return result; }

Sampel ujian 1

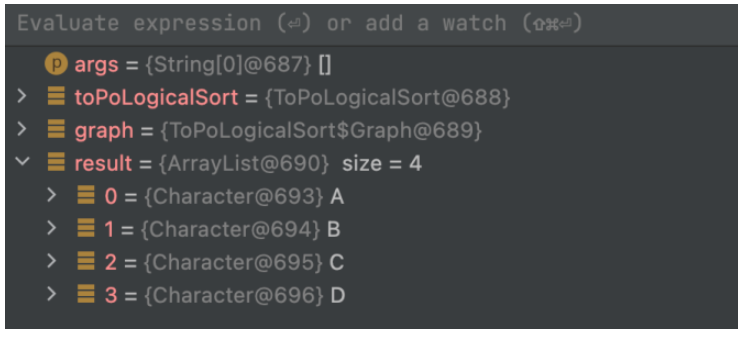
public static void main(String[] args) { ToPoLogicalSort toPoLogicalSort = new ToPoLogicalSort(); //初始化一个图 Graph graph = new Graph(new char[]{'A', 'B', 'C', 'D'}); graph.addEdge(0, 1); graph.addEdge(0,2); graph.addEdge(1,3); graph.addEdge(2,3); List result = toPoLogicalSort.toPoLogicalSort(graph); }

Hasil pelaksanaan

Contoh ujian 2

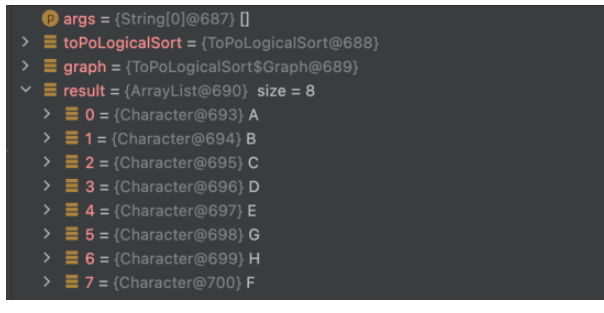
public static void main(String[] args) { ToPoLogicalSort toPoLogicalSort = new ToPoLogicalSort(); //初始化一个图 Graph graph = new Graph(new char[]{'A', 'B', 'C', 'D','E','F','G','H'}); graph.addEdge(0, 1); graph.addEdge(0,2); graph.addEdge(0,3); graph.addEdge(1,4); graph.addEdge(2,4); graph.addEdge(3,4); graph.addEdge(4,7); graph.addEdge(4,6); graph.addEdge(7,5); graph.addEdge(6,7); List result = toPoLogicalSort.toPoLogicalSort(graph); }

Hasil pelaksanaan

Atas ialah kandungan terperinci Bagaimana untuk melaksanakan pengisihan topologi di Jawa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!