
Elektron yang berinteraksi mempamerkan pelbagai fenomena unik pada tenaga dan suhu yang berbeza Jika kita mengubah persekitaran sekelilingnya, mereka akan mempamerkan gelagat kolektif baharu, seperti putaran, turun naik berpasangan, dll. Walau bagaimanapun, Masih terdapat banyak kesukaran. dalam menangani fenomena ini antara elektron. Ramai penyelidik menggunakan Renormalization Group (RG) untuk menyelesaikan masalah ini.
Dalam konteks data berdimensi tinggi, kemunculan teknologi pembelajaran mesin (ML) dan kaedah dipacu data telah menimbulkan minat yang besar dalam kalangan penyelidik dalam fizik kuantum setakat ini, idea ML telah digunakan dalam interaksi sistem elektronik.
Dalam artikel ini, ahli fizik dari Universiti Bologna dan institusi lain menggunakan kecerdasan buatan untuk memampatkan masalah kuantum yang setakat ini memerlukan 100,000 persamaan menjadi satu dengan hanya 4 persamaan, semuanya tanpa mengorbankan ketepatan, penyelidikan itu diterbitkan hari ini dalam Surat Kajian Fizikal.
Alamat kertas: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.136402
Domenico Di Sante, pengarang pertama kajian dan penolong profesor di Universiti Bologna, berkata: Kami menggabungkan projek besar ini bersama-sama dan kemudian menggunakan pembelajaran mesin untuk memadatkannya menjadi sesuatu yang boleh dikira dengan satu jari.
Kajian ini memperkatakan persoalan bagaimana elektron bertindak semasa ia bergerak merentasi kekisi seperti grid. Mengikut pengalaman sedia ada, apabila dua elektron menduduki kekisi kekisi yang sama, mereka akan berinteraksi. Fenomena ini, yang dikenali sebagai model Hubbard, ialah persediaan ideal bagi beberapa bahan yang membolehkan saintis memahami cara tingkah laku elektron mencipta fasa jirim, seperti superkonduktiviti, di mana elektron mengalir melalui bahan tanpa rintangan. Model ini juga boleh berfungsi sebagai tempat ujian untuk kaedah baharu sebelum ia digunakan pada sistem kuantum yang lebih kompleks.
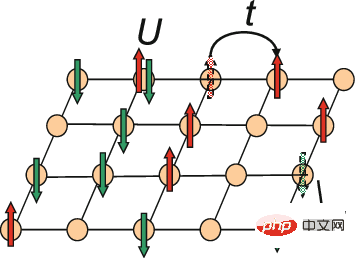
Gambar rajah skematik model Hubbard dua dimensi
The Hubbard model kelihatan mudah. Tetapi walaupun menggunakan kaedah pengkomputeran canggih untuk memproses bilangan elektron yang kecil memerlukan banyak kuasa pengkomputeran. Ini kerana apabila elektron berinteraksi, mereka menjadi kuantum secara mekanikal: walaupun elektron terletak jauh di dalam kekisi, kedua-dua elektron tidak boleh dirawat secara bebas, jadi ahli fizik mesti berurusan dengan mereka semua pada masa yang sama, dan bukannya bekerja dengan satu elektron pada satu masa. Semakin banyak elektron, semakin banyak kuantum mekanikal yang akan berlaku, dan kesukaran pengiraan akan meningkat secara eksponen.
Kaedah biasa untuk mengkaji sistem kuantum ialah kumpulan penormalan semula. Sebagai peranti matematik, ahli fizik menggunakannya untuk memerhati tingkah laku sistem, seperti model Hubbard. Malangnya, kumpulan penormalan semula merekodkan semua gandingan yang mungkin antara elektron, yang mungkin mengandungi beribu-ribu, ratusan ribu, malah berjuta-juta persamaan bebas yang perlu diselesaikan. Selain itu, persamaan adalah kompleks: setiap persamaan mewakili sepasang elektron yang berinteraksi.
Pasukan Di Sante tertanya-tanya sama ada mereka boleh menggunakan alat pembelajaran mesin yang dipanggil rangkaian saraf untuk menjadikan kumpulan penormalan semula lebih mudah diurus.
Dalam kes rangkaian saraf, pertama, penyelidik menggunakan prosedur pembelajaran mesin untuk mewujudkan sambungan kepada kumpulan penormalan semula bersaiz penuh kemudian rangkaian saraf melaraskan kekuatan sambungan ini sehingga ia mencari satu set kecil persamaan yang menghasilkan penyelesaian yang sama seperti kumpulan penormalan semula yang sangat besar yang asal. Kami berakhir dengan empat persamaan, dan walaupun terdapat hanya empat, output program menangkap fizik model Hubbard.
Di Sante berkata: "Rangkaian saraf pada asasnya ialah mesin yang boleh menemui corak tersembunyi, dan hasil ini melebihi jangkaan kami." Melatih program pembelajaran mesin memerlukan banyak kuasa pengkomputeran, jadi mereka mengambil masa beberapa minggu untuk disiapkan. Berita baiknya ialah sekarang program mereka sedang berjalan dan berjalan, beberapa tweak boleh menyelesaikan masalah lain tanpa perlu bermula dari awal.
Apabila bercakap tentang hala tuju penyelidikan masa depan, Di Sante berkata bahawa adalah perlu untuk mengesahkan keberkesanan kaedah baharu itu pada sistem kuantum yang lebih kompleks. Di samping itu, Di Sante berkata terdapat kemungkinan besar untuk menggunakan teknik dalam bidang lain mengenai kumpulan penormalan semula, seperti kosmologi dan neurosains.
Kumpulan penormalan semula fungsi empat dimensi bergantung pada skala (fRG) ciri aliran yang menerangkan ciri-ciri aliran t-t' Hubbard dua dimensi yang dikaji secara meluas pada kristal segi empat sama Fungsi Vertex , para penyelidik melakukan pengurangan dimensi dipacu data. Mereka menunjukkan bahawa seni bina pembelajaran mendalam berdasarkan penyelesai persamaan pembezaan biasa neural (NODE) dalam ruang terpendam berdimensi rendah boleh mempelajari dinamik fRG dengan cekap yang menerangkan pelbagai keadaan superkonduktor magnet dan gelombang d model Hubbard.
Para penyelidik seterusnya mencadangkan analisis penguraian mod dinamik, yang boleh mengesahkan bahawa sebilangan kecil mod sememangnya mencukupi untuk menangkap dinamik fRG. Kajian itu menunjukkan kemungkinan menggunakan kecerdasan buatan untuk mengekstrak perwakilan padat bagi fungsi empat puncak elektron yang berkaitan, yang merupakan matlamat paling penting untuk berjaya melaksanakan kaedah teori medan kuantum termaju dan menyelesaikan masalah banyak elektron.
Objek asas dalam fRG ialah fungsi puncak V(k_1, k_2, k_3), yang pada dasarnya memerlukan pengiraan dan penyimpanan fungsi yang terdiri daripada tiga pembolehubah momentum berterusan. Dengan mengkaji corak teori tertentu, model Hubbard dua dimensi dianggap relevan dengan cuprates dan pelbagai konduktor organik. Kami menunjukkan bahawa perwakilan dimensi yang lebih rendah boleh menangkap aliran fRG bagi fungsi puncak dimensi tinggi. 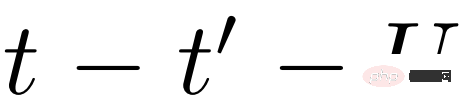
Keadaan dasar fRG model Hubbard. Hamiltonian mikroskopik yang dipertimbangkan oleh penyelidik ditunjukkan dalam formula berikut (1).
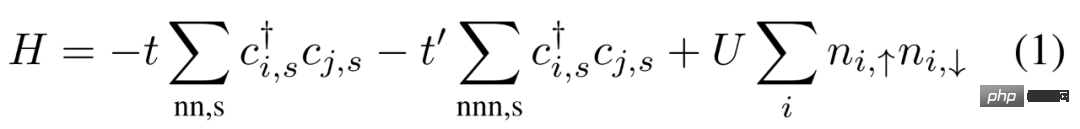
Sifat 2 zarah model Hubbard dikaji melalui skema aliran suhu fRG satu gelung, di mana Aliran RG 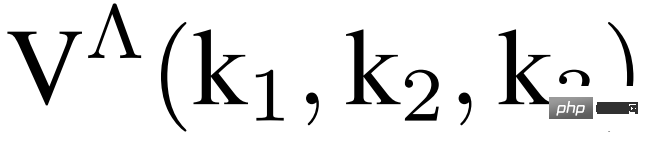 ditunjukkan dalam formula berikut (2).
ditunjukkan dalam formula berikut (2).
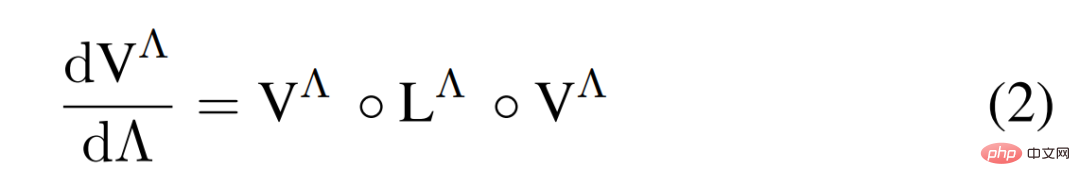
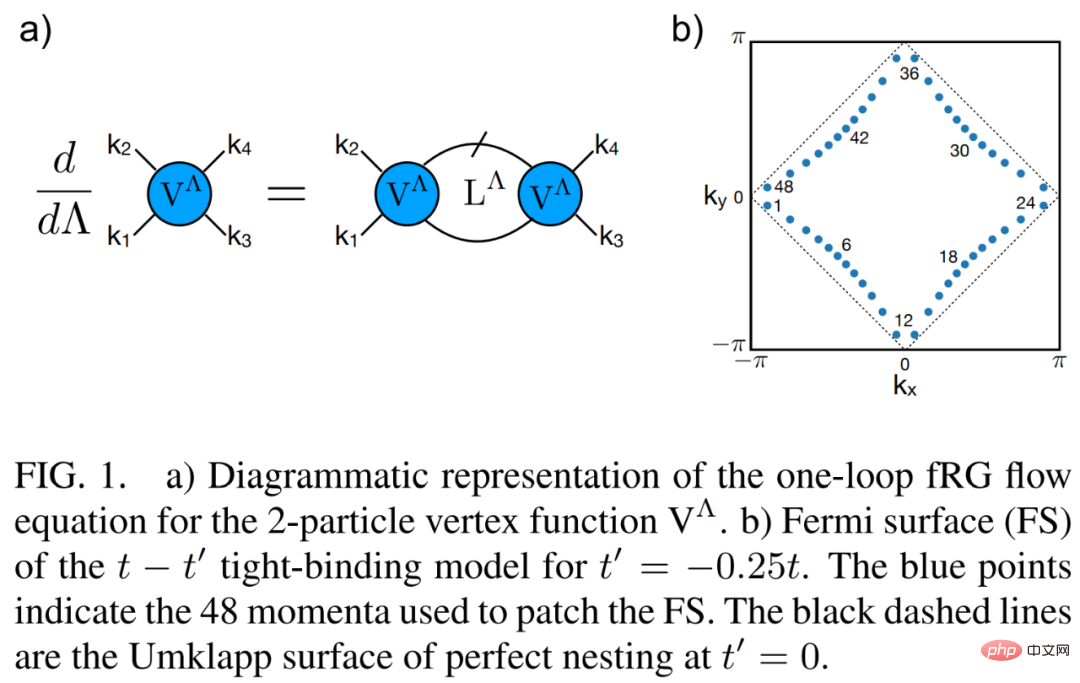
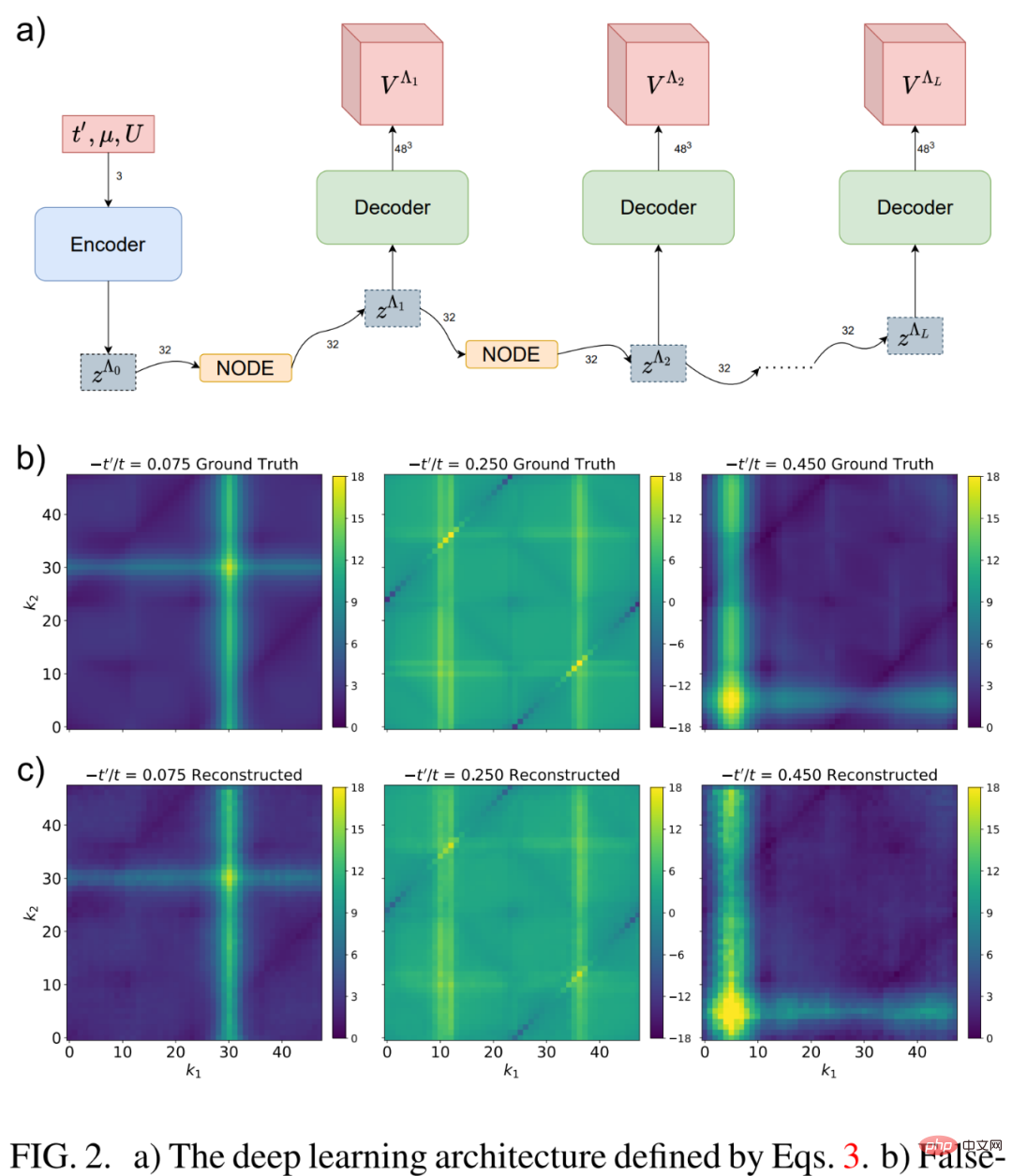
Rajah 1 a) di bawah ialah perwakilan grafik bagi persamaan aliran fRG satu gelang bagi fungsi puncak 2 zarah V^Λ.
Mari kita lihat fRG pembelajaran mendalam. Seperti yang ditunjukkan dalam Rajah 2 b) di bawah, dengan meneliti gandingan 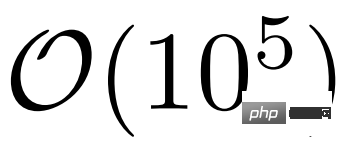 bagi fungsi puncak 2 zarah sebelum aliran fRG cenderung kepada gandingan kuat dan penguraian anggaran satu cincin, penyelidik menyedari bahawa banyak daripada mereka sama ada kekal dalam keadaan tepi Sama ada menjadi tidak relevan di bawah aliran RG.
bagi fungsi puncak 2 zarah sebelum aliran fRG cenderung kepada gandingan kuat dan penguraian anggaran satu cincin, penyelidik menyedari bahawa banyak daripada mereka sama ada kekal dalam keadaan tepi Sama ada menjadi tidak relevan di bawah aliran RG.
Para penyelidik sedang melaksanakan skim pengurangan dimensi fleksibel berdasarkan seni bina NODE berparameter yang sesuai untuk masalah dimensi tinggi semasa Kaedah ini ditunjukkan dalam Rajah 2 a) di bawah, memfokuskan pada saraf dalam rangkaian.
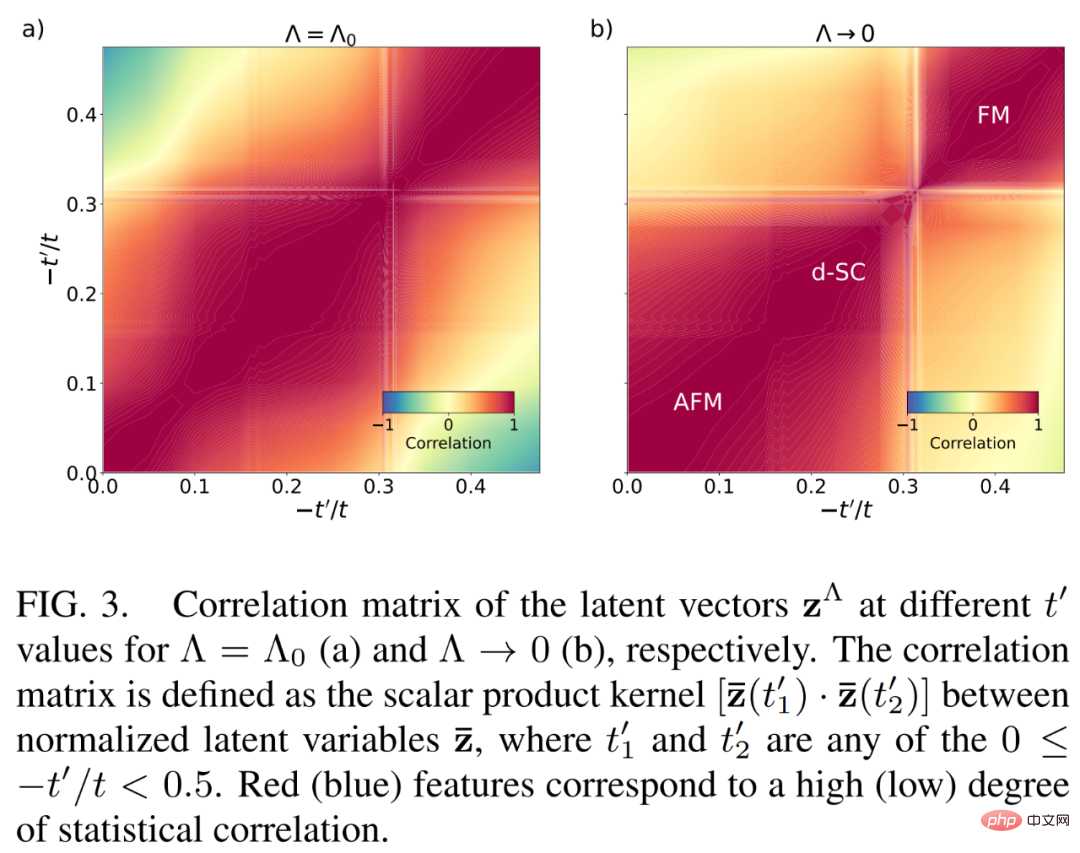
Rajah 3 di bawah menunjukkan tiga perwakilan ruang terpendam yang sangat berkorelasi secara statistik z sebagai saraf NODE semasa dinamik fRG bagi ciri Pembelajaran ruang terpendam Internet.
Sila rujuk kertas asal untuk butiran lanjut.
Atas ialah kandungan terperinci Masalah kuantum yang memerlukan 100,000 persamaan untuk diselesaikan telah dimampatkan oleh AI kepada hanya empat tanpa mengorbankan ketepatan.. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Apakah kaedah pembundaran dalam sql
Apakah kaedah pembundaran dalam sql
 Bagaimana untuk membuka fail html WeChat
Bagaimana untuk membuka fail html WeChat
 Pengenalan kepada perisian lukisan seni bina
Pengenalan kepada perisian lukisan seni bina
 Cara membuat gambar bulat dalam ppt
Cara membuat gambar bulat dalam ppt
 Bagaimana untuk menyelesaikan masalah 400 permintaan buruk apabila halaman web dipaparkan
Bagaimana untuk menyelesaikan masalah 400 permintaan buruk apabila halaman web dipaparkan
 Teknik yang biasa digunakan untuk perangkak web
Teknik yang biasa digunakan untuk perangkak web
 Penggunaan arahan sumber dalam linux
Penggunaan arahan sumber dalam linux
 Bagaimana untuk membuka fail keadaan
Bagaimana untuk membuka fail keadaan




